Производственный менеджмент (лекции). Производственный менеджмент
 Скачать 6.27 Mb.
|
Симплекс-метод решения задачи производственного планированияВсе точные методы решения общей задачи линейного программирования (ОЗЛП) косвенные , т.е. не непосредственно решаем ОЗЛП, а решаем некоторую другую задачу и на основе ее делаем вывод о решении ОЗЛП. Такой косвенной задачей в ЛП является каноническая задача линейного программирования (КЗЛП). Канонической задачей линейного программирования будем называть следующую задачу: F(  ) = ( ) max (min) (1)A =  (2) 0 (3)rang (A) = m < n, (4) где  = (c1, c2, ..., cn)T, = (X1,X2 , ..., Xn)T,A = (aij) m, n = (  , , ...,  ), = (b1, b2, ..., bm)T,  0.Если целевая функция имеет конечный экстремум, то по крайней мере одно оптимальное решение является базисным (вершиной допустимого множества). Это означает, что при поиске оптимального решения в допустимой области можно ограничиться базисными допустимыми решениями. В вычислительной схеме симплекс-метода реализуется вычислительный процесс, при котором, начиная с некоторой допустимой вершины (обычно начала координат), осуществляются последовательные переходы от одной допустимой вершины к другой, до тех пор, пока не будет найдена точка, соответствующая оптимальному плану. Канонический вид, рассмотренной в параграфе 1.2 , задачи производственного планирования будет следующим: F(  ) = 3X1 + 4X2 + 0X3 + 0X4 + 0X5 maxпри ограничениях X1 + X2 + X3 = 5 2X1 + X2 + X4 = 9 X1 + 2X2 +X5 = 7 Xj 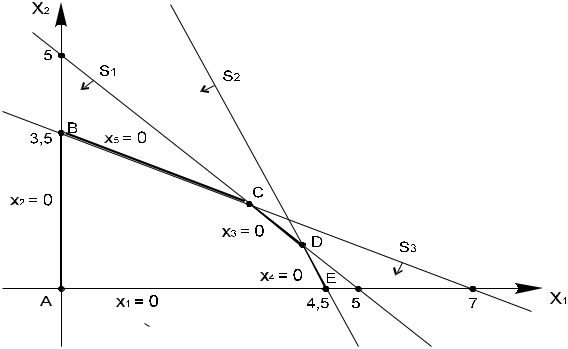0, j = 1, ..., 5. Рис. 1 Геометрическая интерпретация задачи производственного планирования Каждую точку пространства решений можно определить с помощью переменных X1, X2, X3, X4, X5. Увеличение переменных X3, X4, X5 будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область. Нас интересует прежде всего алгебраическое представление вершин допустимого множества. Анализируя рисунок можно записать:
Смежные вершины (крайние точки) отличаются только одной переменной в каждой группе свободных и базисных переменных. Все допустимые вершины определяются как все неотрицательные базисные решения системы линейных уравнений (2). Расширенную матрицу системы линейных уравнений, которая определяет неотрицательное базисное решение исходной системы будем называть К-матрицей. Пусть  = ( , , ...,  ) - базисная подматрица , т.е. матрица составленная из столбцов ( , , ...,  ) матрицы  , образующих на s-й итерации симплекс-метода единичную подматрицу.Матрица K(S) может быть получена следующим образом:  .Тогда  .В нашей задаче 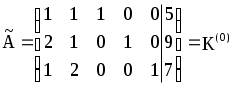 , ,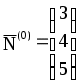  , 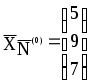 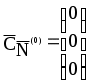.K(0) определяет исходный опорный план. Это вершина А на рис. 1. Приведем решение, рассмотренной выше, задачи в симплекс-таблице. Таблица 1
Из последней итерации симплексной таблицы можно получить информацию относительно оптимального плана, статуса сырья, ценности сырья, чувствительности базиса к изменению запасов сырья и вариациям коэффициентов целевой функции. а) оптимальное решение. Используя данные симплекс-таблицы основные результаты можно представить в следующем виде:  = (3, 2, 0, 1, 0),X1 = 3 - объем производства продукции вида А1, X2 = 2 - объем производства продукции вида А2, F(  )= 17 - прибыль от реализации продукции.б) статус видов сырья. Сырье S1 - дефицитное, так как значение остаточной переменной X3 равно нулю. Сырье S2 - недефицитное, так как значение остаточной переменной X4 равно единице. Положительное значение остаточной переменной указывает на неполное использование соответствующего вида сырья. Сырье S3 - дефицитное, так как значение остаточной переменной X5 равно нулю. Увеличение запасов сырья S1 и S3 позволит улучшить найденное решение. в) ценность сырья. Ценность различных видов сырья характеризуется величиной улучшения оптимального значения F(  ), приходящегося на единицу прироста соответствующего вида сырья: ,  .Как следует из теории линейного программирования ценность видов сырья можно определить по формуле:  , , где - номер единичного столбца с единицей на i-м месте в матрице  , - коэффициент при переменной  в целевой функции, - симплексная разность при переменной в последней итерации.В нашем примере: Y1 = 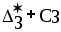 = 2 + 0 = 2 Y2 = 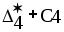 = 0 + 0 = 0Y3 = 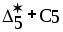 = 1 + 0 = 1.г) чувствительность базиса к изменению запасов сырья. Предположим, что запас первого вида сырья изменился на 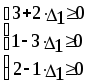 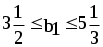, т.е. теперь он составляет 5+ единиц. Введение скажется только на правой части симплекс-таблицы. Все же изменения правой части можно непосредственно определить по данным симплекс-таблицы. А именно, коэффициенты при в правых частях ограничений будут равны коэффициентам при первой остаточной переменной, т.е. при переменной X3. Так как изменение запаса сырья может повлиять на допустимость базисного решения, то величина должна быть ограничена решением системы неравенств:  -3/2  1/3 или ( ) .В данном диапазоне изменения запаса сырья S1 переменные X1, X4, X2 остаются базисными и определяют оптимальное базисное решение. В этом случае остаются неизменными виды производственной деятельности. При исследовании чувствительности базиса к изменению запасов сырья S2 и S3 поступим аналогично. Соответственно получим: 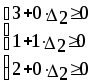 ,  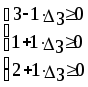 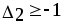,   ,  .Так как изменение запасов сырья может повлиять только на допустимость решения, то интервалы изменения запасов сырья в общем случае определятся из соотношений: 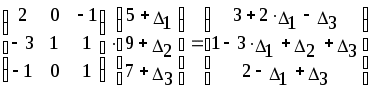   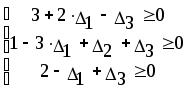 ,  .д) чувствительность оптимального плана к вариациям коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на симплексные разности, то такие изменения могут сделать полученное решение неоптимальным. Предположим, что коэффициент  изменился на  , а коэффициент  остался без изменения, т.е.F( )=  Симплексные разности при базисных переменных X1, X4, X2 останутся равными нулю. Коэффициенты при 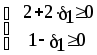в симплексных разностях небазисных переменных X3 и X5 будут равны коэффициентам при этих переменных в уравнении соответствующем базисной переменной X1, так как именно при этой переменной изменился коэффициент. Таким образом получим  ,  .Аналогично для случая F( ) =  получим 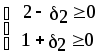  ,  .Любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплексной таблице изменяется только симплексная разность соответствующей этой переменной. В таком случае необходимо требовать  , если изменился коэффициент при k-й переменной.Изменение коэффициентов целевой функции оказывает влияние на оптимальность полученного ранее решения. Поэтому допустимые интервалы изменения коэффициентов целевой функции в общем случае определятся из следующих соотношений: 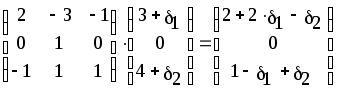 . 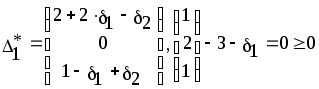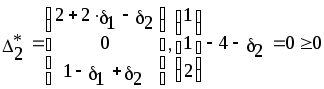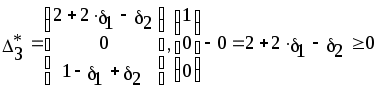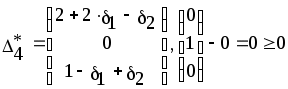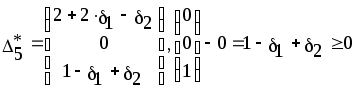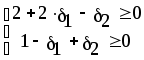=  . , , , , ,  .Альтернативные оптимальные решенияКогда гиперплоскость, представляющая целевую функцию, параллельна гиперплоскости, соответствующей связывающему ограничению ( которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение в некоторой совокупности точек пространства решений. Такие решения называются альтернативными оптимальными решениями. Приводимый ниже пример рассматриваемой ситуации показывает, что при этом обычно существует бесконечное множество альтернативных решений. Пример: F(  )= 2x1 + 4x2 maxпри ограничениях x1 + 2x2 5 (ресурс 1) x1 + x2 4 (ресурс 2) x1 0, x2 0. Рис.2 иллюстрирует условия данной задачи ЛП, особенность которой состоит в том, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей одному из связывающих ограничений. 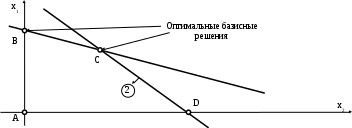 Рис. 2. Геометрическая интерпретация альтернативных базисных решений Это обусловливает наличие альтернативных оптимальных решений. Любая точка отрезка ВС представляет собой альтернативный оптимум, причем в каждой из этих точек целевая функция имеет одно и то же оптимальное значение. Приведем решение задачи в симплекс-таблице. Таблица 2
Каким образом по результатам итерации можно узнать о наличии альтернативных решений? Нулевое значение симплексной разности у небазисной переменной свидетельствует о том, что ее включение в базис не изменит значения целевой функции, но приведет к изменению других переменных. Любое решение, соответствующее точке (  , ) принадлежащей отрезку ВС, можно определить как положительно-взвешенное среднее двух полученных оптимальных базисных решений, соответствующих точкам В и С. Поэтому, используя координаты точек В и СВ: х1 = 0; х2 = 5/2; С: х1 = 3; х2 = 1; и полагая  , можно выразить координаты любой точки отрезка ВС следующим образом: , .Информация о наличии альтернативных оптимумов дает возможность выбора альтернативного варианта в наибольшей степени отвечающего сложившейся производственной ситуации. Метод искусственного базисаЧасто, после приведения ОЗЛП к каноническому виду расширенная матрица системы линейных уравнений (СЛУ) не является К-матрицей (нет начального опорного плана), и, следовательно, решать такую КЗЛП симплекс-методом нельзя. Суть метода искусственного базиса состоит в следующем: строится такая вспомогательная КЗЛП (ВКЗЛП) с заранее известным опорным планом, по решению которой либо определяется начальный опорный план исходной задачи, либо устанавливается, что ее множество планов пусто. Дано:  , i = 1, ..., m, rang (A) = m < n, bi 0, i = 1, ..., m.Найти: К-матрицу (начальный опорный план). Построим следующую ВКЗЛП:  ,   , i = 1, ..., m, xj 0, j = 1, ..., n, yi 0, i = 1, ..., m, yi – искусственные переменные.Очевидно, начальный опорный план ВКЗЛП имеет вид:  , = (n+1, n+2, ..., n+m).Применяя симплекс-метод, находят  – решение ВКЗЛП.Замечание: ВКЗЛП всегда разрешима, так как множество ее планов не пусто, а целевая функция ограничена. Теорема: Если  , то  – начальный опорный план исходной КЗЛП. Если  , то множество планов исходной КЗЛП пусто и, следовательно, она неразрешима.Пример: F(X) = 5x1 + 3x2 + 4x3 - x4  x1 + 3x2 + 2x3 + 2x4 = 3 2x1 + 2x2 + x3 + x4 = 3  . x1 + 3x2 + 2x3 + 2x4 + y1 = 3 x1 + 3x2 + 2x3 + 2x4 + y2 = 3 xj 0, j = 1, ..., 4, y1,2 0.  = (5,6),  = (3,3),  = (-1,-1).Таблица 1
Замечание: По мере выхода искусственных переменных из базиса, вычисления в соответствующих клетках симплекс-таблицы не проводятся. Получили оптимальный опорный план ВКЗЛП.  (3/4,3/4,0,0,0,0), ,  (3/4,3/4,0,0).Теперь решаем симплекс-методом исходную задачу: F(X)= 5x1 + 3x2 + 4x3 - x4 x2 + 3/4x3 + 3/4x4 = 3/4 x1 - 1/4x3 - 1/4x4 = 3/4 xj 0, j = 1, ..., 4.Таблица 2
 (1, 0, 1, 0),  = 9.Анализ решаемых задачМатематическая модель является хорошим средством получения ответов на широкий круг самых разнообразных вопросов, возникающих при принятии оптимальных решений. Например, на этапе постановки задачи часто производится анализ с целью ответа на вопросы: “что будет, если...?“ и/или “что надо, чтобы...?”. Анализ с целью ответа на первый вопрос называется вариантным анализом; на второй - решениями по заказу. Для задач распределения ресурсов большой интерес представляет решение задачи минимизации используемых ресурсов при заданном результате. Рассмотрим следующую исходную задачу: Первая постановка: F( )= 4 X1 + 3 X2 + 6 X3 + 7 X4  (прибыль)при ограничениях на ресурсы 2 X1 + X2 + X3 + X4 280 - ( трудовые) X1 + X3 + X4 80 - (сырье)X1 + 2 X2 + X3 250 - (финансы)Xj  0, j=1,...,4 .Решив задачу получим: = (0, 125, 0, 80) , гдеX1 = 0 - объем производства продукции вида 1, X2 = 125 - объем производства продукции вида 2, X3 = 0 - объем производства продукции вида 3, X4 = 80 - объем производства продукции вида 4. F( ) = 935 - прибыль от реализации продукции.Вторая постановка: F( )= 4 X1 + 3 X2 + 6 X3 + 7 X4 (прибыль)при ограничениях на ресурсы 2 X1 + X2 + X3 + X4 280 - ( трудовые) X1 + X3 + X4 80 - (сырье)X1 + 2 X2 + X3 250 - (финансы)X1 10 , X2 100, - (дополнительные X3 25 , ограничения наX4 50 выпуск продукции)Xj 0, j=1,...,4.В результате решения получим: = (10, 100, 25, 45) , F( ) = 805.Третья постановка: F(  ) = Y1 + Y2 + Y3 (минимизация используемого ресурса)2 X1 + X2 + X3 + X4 + Y1 = 280 - ( трудовые) X1 + X3 + X4 + Y2 = 80 - (сырье) X1 + 2 X2 + X3 + Y3 = 250 - (финансы)X1 10 , X2 20 - (задаваемыйX3 25 , X4 40. результат)Y1 , Y2 , Y3 0 - ( неиспользованный ресурс).Решив задачу получим: = (10, 20, 25, 40) ,  = (175, 5, 175).При решении по заказу пользователь задает значения тех величин, которые он хочет иметь в оптимальном решении. Такие задачи могут быть трех видов: 1) назначение величины целевой функции; 2) назначение величин искомых переменных; 3) назначение величин используемых ресурсов. Следует иметь в виду, что во всех этих случаях возможно появление несовместного решения. Рассмотрим такую ситуацию на нашем примере. Четвертая постановка: F( )= 4 X1 + 3 X2 + 6 X3 + 7 X4 (прибыль)при ограничениях на ресурсы 2 X1 + X2 + X3 + X4 280 - ( трудовые) X1 + X3 + X4 80 - (сырье)X1 + 2 X2 + X3 250 - (финансы)X1 100 , X2 100, - (дополнительные X3 = 30 , X4 = 70 ограничения на выпуск продукции) Xj 0, j=1,...,4 .Очевидно, что для выпуска такого количества продукции располагаемых ресурсов будет недостаточно. Найдем минимальные значения дополнительных необходимых ресурсов каждого вида позволяющих удовлетворить ограничениям задачи. Пятая постановка: F( ) = t1 + t2 + t3  (минимизация необходимого дополнительного ресурса)2 X1 + X2 + X3 + X4 - t1 = 280 - ( трудовые) X1 + X3 + X4 - t2 = 80 - (сырье) X1 + 2 X2 + X3 - t3 = 250 - (финансы)X1 100 , X2 100, - (задаваемый результат)X3 = 30 , X4 = 70. t1 , t2 , t3 0 - (дополнительный ресурс).Решив задачу получим: = (100, 60, 30, 70) ,  = (80, 120, 0). |
=
=
=
