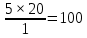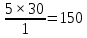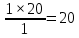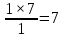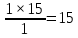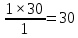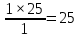Управление и организация. Люсая А.В. 5 вариант_Принято. 94 балла. Зачтено.. Производственный процесс и его организация. Система сетевого планирования и управления. Организация работы энергетического хозяйства

• Название: Производственный процесс и его организация. Система сетевого планирования и управления. Организация работы энергетического хозяйства
• Анкор: Управление и организация
• Дата: 15.11.2020
• Размер: 262.04 Kb.
• Имя файла: Люсая А.В. 5 вариант_Принято. 94 балла. Зачтено..docx
• Тип: Документы; #150573

Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «СЕВЕРО-ВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ М.К.АММОСОВА» Технический институт (филиал) ФГАОУ ВО «СВФУ» в г. Нерюнгри

Кафедра электропривода и автоматизации производственных процессов


Расчетно-графическая работа

По дисциплине «Управление и организация производства»

5 вариант

Выполнил студент(ка):

Группы ЭП-18(5)

Люсая А.В.

Проверил преподаватель:

Профессор

Мартыненко Н.К.


Нерюнгри 2020г.

Тема: «Производственный процесс и его организация.

Система сетевого планирования и управления.

Организация работы энергетического хозяйства».

Задание №1

Задано время операций по обработке партии из 5 изделий.

Таблица 1

№ операции	Вариант времени операций
	5
1	20
2	9
3	7
4	15
5	30
6	35
7	16
8	25
9	15

Построить графики операционного цикла для последовательного, параллельного и параллельно-последовательного движения партии.

Решение

(1)


Расчет длительности технологического цикла при последовательном виде движений предметов труда.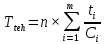


(2)
Таблица 2

Номер операции	ti, мин	Ci
1	20	1
2	9	1
3	7	1
4	15	1
5	30	1
6	35	1
7	16	1
8	25	1
9	15	1

Построение графика длительности производственного цикла при последовательном виде движений предметов труда.



Рис. - График длительности производственного цикла при последовательном виде движений

(3)

Расчет длительности технологического цикла при параллельном виде движений предметов труда.
(4)

Таблица 3

Номер операции	ti	Ci
1	20	1
2	9	1
3	7	1
4	15	1
5	30	1
6	35	1
7	16	1
8	25	1
9	15	1

Построение графика длительности производственного цикла при последовательно-параллельном виде движений предметов труда.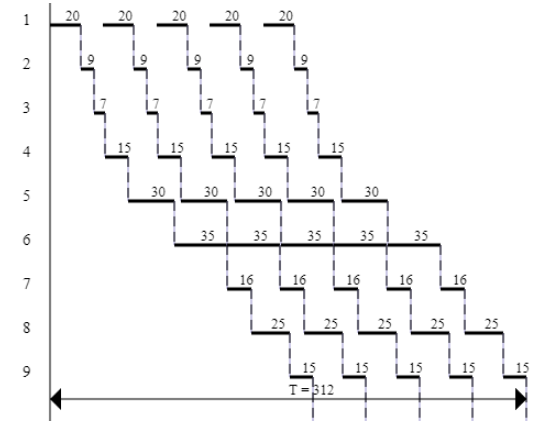




Рис. - График длительности производственного цикла при последовательно-параллельном виде движений

(5)
Расчет длительности технологического цикла при параллельно–последовательном виде движений предметов труда.


























(6)


Таблица 4

Номер операции	ti	Ci
1	20	1
2	9	1
3	7	1
4	15	1
5	30	1
6	35	1
7	16	1
8	25	1
9	15	1

Построение графика длительности производственного цикла при последовательно-параллельном виде движений предметов труда.



Рис. - График длительности производственного цикла при последовательно-параллельном виде движений

Задание №2

Задача 2.1



Параметры работ

Таблица 1

Работа	Время
0,1	6
0,3	5
0,5	2
1,2	1
1,3	3
1,4	7
2,7	9
3,4	2
3,5	7
3,6	5
4,6	4
4,7	1
5,6	7
5,8	2
5,9	9
6,7	4
6,8	2
6,9	8
6,10	6
7,10	4
8,9	1
8,10	3
8,11	9
10,11	8

Задание

расчитать временные параметры сетевого графика (среднее время выполнения работы, раннего и позднего сорока свершения событий);

1. 
   определить полный и свободный резерв времени выполнения работ;
   
2. 
   определить критический путь сетевого графика, выделить его на рисунке.
   

Решение

Расчет сроков свершения событий.
Для i=0 (начального события), очевидно tp(0)=0.
i=1: t^p(1) = t^p(0) + t(0,1) = 0 + 6 = 6.
i=2: t^p(2) = t^p(1) + t(1,2) = 6 + 1 = 7.
i=3: max(t^p(0) + t(0,3); t^p(1) + t(1,3)) = max(0 + 5;6 + 3) = 9.
i=4: max(t^p(1) + t(1,4); t^p(3) + t(3,4)) = max(6 + 7;9 + 2) = 13.
i=5: max(t^p(0) + t(0,5); t^p(3) + t(3,5)) = max(0 + 2;9 + 7) = 16.
i=6: max(t^p(3) + t(3,6); t^p(4) + t(4,6); t^p(5) + t(5,6)) = max(9 + 5; 13 + 4; 16 + 7) = 23.
i=7: max(t^p(2) + t(2,7); t^p(4) + t(4,7); t^p(6) + t(6,7)) = max(7 + 9; 13 + 1; 23 + 4) = 27.
i=8: max(t^p(5) + t(5,8); t^p(6) + t(6,8)) = max(16 + 2;23 + 2) = 25.
i=9: max(t^p(5) + t(5,9); t^p(6) + t(6,9); t^p(8) + t(8,9)) = max(16 + 9; 23 + 8; 25 + 1) = 31.
i=10: max(t^p(6) + t(6,10); t^p(7) + t(7,10); t^p(8) + t(8,10); t^p(9) + t(9,10)) = max(23 + 6;27 + 4; 25 + 3; 31 + 0) = 31.
i=11: max(t^p(8) + t(8,11); t^p(10) + t(10,11)) = max(25 + 9; 31 + 8) = 39.
Длина критического пути равна раннему сроку свершения завершающего события 11: t_kp=tp(11)=39
При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).
Для i=11 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(11)= t^р(11)=39
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Просматриваются все строчки, начинающиеся с номера 10.
i=10: t^п(10) = t^п(11) - t(10,11) = 39 - 8 = 31.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Просматриваются все строчки, начинающиеся с номера 9.
i=9: t^п(9) = t^п(10) - t(9,10) = 31 - 0 = 31.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.
i=8: min(t^п(9) - t(8,9); t^п(10) - t(8,10); t^п(11) - t(8,11)) = min(31 - 1; 31 - 3; 39 - 9) = 28.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7.
i=7: t^п(7) = t^п(10) - t(7,10) = 31 - 4 = 27.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.
i=6: min(t^п(7) - t(6,7); t^п(8) - t(6,8); t^п(9) - t(6,9); t^п(10) - t(6,10)) = min(27 - 4; 28 - 2; 31 - 8; 31 - 6) = 23.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.
i=5: min(t^п(6) - t(5,6); t^п(8) - t(5,8); t^п(9) - t(5,9)) = min(23 - 7; 28 - 2; 31 - 9) = 16.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.
i=4: min(t^п(6) - t(4,6); t^п(7) - t(4,7)) = min(23 - 4;27 - 1) = 19.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.
i=3: min(t^п(4) - t(3,4); t^п(5) - t(3,5); t^п(6) - t(3,6)) = min(19 - 2; 16 - 7; 23 - 5) = 9.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.
i=2: t^п(2) = t^п(7) - t(2,7) = 27 - 9 = 18.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.
i=1: min(t^п(2) - t(1,2); t^п(3) - t(1,3); t^п(4) - t(1,4)) = min(18 - 1; 9 - 3; 19 - 7) = 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 0. Просматриваются все строчки, начинающиеся с номера 0.
i=0: min(t^п(1) - t(0,1); t^п(3) - t(0,3); t^п(5) - t(0,5)) = min(6 - 6; 9 - 5; 16 - 2) = 0.

Таблица 2 -Расчет резерва событий

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
0		0	0
1	6	6	0
2	7	18	11
3	9	9	0
4	13	19	6
5	16	16	0
6	23	23	0
7	27	27	0
8	25	28	3
9	31	31	0
10	31	31	0
11	39	39	0

Заполнение таблицы 3.

Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 0, затем с номера 1 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (1,2) в графу 1 поставим число 1, т.к. на номер 1 оканчиваются 1 работы: (0,1).
Графу 4 получаем из таблицы 1 (t^p(i)). Графу 7 получаем из таблицы 1 (t^п(i)).
Значения в графе 5 получаются в результате суммирования граф 3 и 4.
В графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
Содержимое графы 8 (полный резерв времени R(ij)) равно разности граф 6 и 4 или граф 7 и 5. Если R(ij) равен нулю, то работа является критической
Полный резерв пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ, принадлежащих данному пути, при условии, что срок выполнения всего комплекса работ не изменится. Образовывается, когда предшествующие работы закончатся в свой наиболее ранний срок.


Находим полный резерв R^П_i-j = Tп_j-t_i-j-Tр_i

R^П_(0,1) = 6-6-0 = 0
R^П_(0,3) = 9-5-0 = 4
R^П_(0,5) = 16-2-0 = 14
R^П_(1,2) = 18-1-6 = 11
R^П_(1,3) = 9-3-6 = 0
R^П_(1,4) = 19-7-6 = 6
R^П_(2,7) = 27-9-7 = 11
R^П_(3,4) = 19-2-9 = 8
R^П_(3,5) = 16-7-9 = 0
R^П_(3,6) = 23-5-9 = 9
R^П_(4,6) = 23-4-13 = 6
R^П_(4,7) = 27-1-13 = 13
R^П_(5,6) = 23-7-16 = 0
R^П_(5,8) = 28-2-16 = 10
R^П_(5,9) = 31-9-16 = 6
R^П_(6,7) = 27-4-23 = 0
R^П_(6,8) = 28-2-23 = 3
R^П_(6,9) = 31-8-23 = 0
R^П_(6,10) = 31-6-23 = 2
R^П_(7,10) = 31-4-27 = 0
R^П_(8,9) = 31-1-25 = 5
R^П_(8,10) = 31-3-25 = 3
R^П_(8,11) = 39-9-25 = 5
R^П_(9,10) = 31-0-31 = 0
R^П_(10,11) = 39-8-31 = 0


Свободный резерв времени также можно найти и по формуле R^C_i-j = Tп_i-t_i-j-Tр_i

R^C_(0,1) = 6-6-0 = 0
R^C_(0,3) = 9-5-0 = 4
R^C_(0,5) = 16-2-0 = 14
R^C_(1,2) = 7-1-6 = 0
R^C_(1,3) = 9-3-6 = 0
R^C_(1,4) = 13-7-6 = 0
R^C_(2,7) = 27-9-7 = 11
R^C_(3,4) = 13-2-9 = 2
R^C_(3,5) = 16-7-9 = 0
R^C_(3,6) = 23-5-9 = 9
R^C_(4,6) = 23-4-13 = 6
R^C_(4,7) = 27-1-13 = 13
R^C_(5,6) = 23-7-16 = 0
R^C_(5,8) = 25-2-16 = 7
R^C_(5,9) = 31-9-16 = 6
R^C_(6,7) = 27-4-23 = 0
R^C_(6,8) = 25-2-23 = 0
R^C_(6,9) = 31-8-23 = 0
R^C_(6,10) = 31-6-23 = 2
R^C_(7,10) = 31-4-27 = 0
R^C_(8,9) = 31-1-25 = 5
R^C_(8,10) = 31-3-25 = 3
R^C_(8,11) = 39-9-25 = 5
R^C_(9,10) = 31-0-31 = 0
R^C_(10,11) = 39-8-31 = 0


Независимый резерв времени также можно найти и по формуле R^Н_i-j = Tр_j-t_i-j-Tп_i

R^Н_(0,1) = 6-6-0 = 0
R^Н_(0,3) = 9-5-0 = 4
R^Н_(0,5) = 16-2-0 = 14
R^Н_(1,2) = 7-1-6 = 0
R^Н_(1,3) = 9-3-6 = 0
R^Н_(1,4) = 13-7-6 = 0
R^Н_(2,7) = 27-9-18 = 0
R^Н_(3,4) = 13-2-9 = 2
R^Н_(3,5) = 16-7-9 = 0

R^Н_(3,6) = 23-5-9 = 9
R^Н_(4,6) = 23-4-19 = 0
R^Н_(4,7) = 27-1-19 = 7
R^Н_(5,6) = 23-7-16 = 0
R^Н_(5,8) = 25-2-16 = 7
R^Н_(5,9) = 31-9-16 = 6
R^Н_(6,7) = 27-4-23 = 0
R^Н_(6,8) = 25-2-23 = 0
R^Н_(6,9) = 31-8-23 = 0
R^Н_(6,10) = 31-6-23 = 2
R^Н_(7,10) = 31-4-27 = 0
R^Н_(8,9) = 31-1-28 = 2
R^Н_(8,10) = 31-3-28 = 0
R^Н_(8,11) = 39-9-28 = 2
R^Н_(9,10) = 31-0-31 = 0
R^Н_(10,11) = 39-8-31 = 0

Таблица 3 - Анализ сетевой модели по времени

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tijР.Н.	Ранние сроки: окончание tijР.О.	Поздние сроки: начало tijП.Н.	Поздние сроки: окончание tijП.О.	Резервы времени: полный RijП	Независимый резерв времени RijН	Частный резерв I рода, Rij1	Частный резерв II рода, RijC
(0,1)	0	6	0	6	0	6	0	0	0	0
(0,3)	0	5	0	5	4	9	4	4	4	4
(0,5)	0	2	0	2	14	16	14	14	14	14
(1,2)	1	1	6	7	17	18	11	0	11	0
(1,3)	1	3	6	9	6	9	0	0	0	0
(1,4)	1	7	6	13	12	19	6	0	6	0
(2,7)	1	9	7	16	18	27	11	0	0	11
(3,4)	2	2	9	11	17	19	8	2	8	2
(3,5)	2	7	9	16	9	16	0	0	0	0
(3,6)	2	5	9	14	18	23	9	9	9	9
(4,6)	2	4	13	17	19	23	6	0	0	6
(4,7)	2	1	13	14	26	27	13	7	7	13
(5,6)	2	7	16	23	16	23	0	0	0	0
(5,8)	2	2	16	18	26	28	10	7	10	7
(5,9)	2	9	16	25	22	31	6	6	6	6
(6,7)	3	4	23	27	23	27	0	0	0	0
(6,8)	3	2	23	25	26	28	3	0	3	0
(6,9)	3	8	23	31	23	31	0	0	0	0
(6,10)	3	6	23	29	25	31	2	2	2	2
(7,10)	3	4	27	31	27	31	0	0	0	0
(8,9)	2	1	25	26	30	31	5	2	2	5
(8,10)	2	3	25	28	28	31	3	0	0	3
(8,11)	2	9	25	34	30	39	5	2	2	5
(9,10)	3	0	31	31	31	31	0	0	0	0
(10,11)	4	8	31	39	31	39	0	0	0	0

Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R₁ - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R₁ находится по формуле:
R(i,j)= R^п(i,j) - R(i)
Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:
R(i,j)= R^п(i,j) - R(j)
Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации.
Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле:
R(i,j)= R^п(i,j)- R(i) - R(j)

В данном случае имеются несколько критических путей:
Критический путь №1: (0,1)(1,3)(3,5)(5,6)(6,7)(7,10)(10,11)
Критический путь №2: (0,1)(1,3)(3,5)(5,6)(6,9)(9,10)(10,11)
Продолжительность критического пути: 39Анализ сетевого графика
Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:
K_c = n_pab / n_cob
где K_c – коэффициент сложности сетевого графика; n_pab – количество работ, ед.; n_cob – количество событий, ед.
Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.
K_c = 25 / 12 = 2.08
Поскольку 1.51 < Kc < 2, то сетевой график является средней сложности.





Задача 2.2

Установить потребность предприятия в электроэнергии по данным таблицы

Изделие	Технологическая норма расхода электроэнергии на 1 шт., кВт	Выпуск продукции по вариантам, тыс.шт.
		5
А	2	350
Б	4	100
В	3	250

Коэффициент полезного действия – 0,8; потерь электроэнергии в сети – 0,099.
Решение

1. 
   Определим переменную (зависимую) часть расходов электроэнергии:
   

А=2×350×0,8×0,09=55,44

Б=4×100×0,8×0,099=31,68

В=3×250×0,8×0,099=59,4

2. 
   Определим общую потребность в электроэнергии предприятия: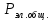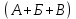
   

= /(0,8×0,099)=(55,44+31,68+59,4)/

/(0,8×0,099)=146,52/0,0792=24 621 212 кВт=1850 МВт.
Ответ: Общую потребность в электроэнергии предприятия


СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 
   Акчурина, А.М. Планирование и организация производства / А.М. Акчурина. - М.: Русайнс, 2017. - 64 c.
   
2. 
   Организация и планирование производства / Под ред. Балакина М.Ф., Рязанова В.А. - М.: Academia, 2018. - 736 c.
   
3. 
   Сыров, В.Д. Организация производства: Учебное пособие / В.Д. Сыров. - М.: Риор, 2018. - 67 c.
   
4. 
   Фатхутдинов, Р.А. Организация производства: Учебник / Р.А. Фатхутдинов. - М.: Инфра-М, 2015. - 216 c.