Курсовая. Пропорциональноинтегральнодифференциальный регулятор для робота на базе микроконтроллера Arduino и легоEV3
 Скачать 155.95 Kb. Скачать 155.95 Kb.
|
|
Пропорционально-интегрально-дифференциальный регулятор для робота на базе микроконтроллера Arduino и легоEV3 (Слайд2) В рамках данной научно исследовательской работы рассматривалась классическая задача движения робота по линии, окрашенной в произвольный цвет. В таких задачах робот должен работать автономно и проходить заданную траекторию за минимальное время. Для решения поставленной задачи существует различные методы. В работе приводится исследование существующих алгоритмов, а так же представлена реализация выбранного алгоритма. (Слайд3) Алгоритмы движения по линии Для начала рассмотрим самый простой алгоритм движения робота по линии ШАГ1. Датчики робота «видят» белое поле. Контроллер принимает решение включить оба мотора и двигаться прямо. ШАГ2. Робот правым датчиком наезжает на черную линию. Для выравнивания положения необходимо притормозить правое колесо. ШАГ3. Робот наезжает левым датчиком на черную линию. Для выравнивания положения необходимо притормозить вращение левого колеса. У этого алгоритма очень большие потери в кпд, он постоянно сбивается и движется крайне неуверенно Пропорциональный регулятор(П-регулятор) Очень популярен для управления движением по линии из-за стабильной работы и простоты его реализации, но у данного алгоритма есть и свои минусы. Первое, робот не может двигаться на большой скорости, не обрабатывает резкие повороты. Алгоритм -опрашиваем показание датчика В случае движения робота с левой стороны от линии вычитаем из полученного значения среднее значение серого В случае движения робота с правой стороны от линии вычитаем из среднего значения серого полученное значение Результат умножаем на коэффициент Полученное число подаем на управление моторов А теперь рассмотрим Пид ЧТО ТАКОЕ ПИД-РЕГУЛИРОВАНИЕ? Алгоритм управления ПИД-регулятором назван в честь трех корректирующих устройств, сумма которых составляет управляемую переменную MB. Пропорциональные, интегральные и производные термины суммируются для расчета выходного сигнала ПИД-регулятора Сначала мы используем показания датчика инфракрасного света, чтобы знать, «насколько далеко находится робот по отношению к линии». На этом «расстоянии от расстояния» мы будем называть это «Ошибка». Затем мы возьмем «количественную оценку этой ошибки», и с помощью математического алгоритма, который мы опишем, мы будем управлять двигателями с разной скоростью, чтобы он всегда адаптировался, чтобы быть выровненным с дорогой. Тогда первое, что мы должны сделать, это получить положение робота от считывания инфракрасных датчиков: Будем использовать датчики QTR-8A. Проведя опыт, мы получаем показания датчиков 1023, когда поверхность абсолютно белая, получаем 0, когда поверхность абсолютно черная. Теперь представьте, что мы используем 8 датчиков инфракрасного света, доступных в матрице. Поднеся их к линии мы получим такие показания: Как мы видим измерения на белом дают 1023, а те, что находятся между черным и белым дают нам значение от 0 до 1023, в зависимости от уровня отражения . Построим диаграмму Из этой диаграммы мы видим, что черная линия находится между четвертым и пятым датчиками, но мы должны получить точное значение положения линии, и для жтого мы сделаем преобразование данных К полученным значениям мы изменим диапозон от 0 до 1023 на от 0 до 1000. Так же мы их перевернем, то есть, раньше было 1000 теперь 0 и получим следующий график Теперь мы можем графически наблюдать, где расположена черная линия Но нам нужны точные данные и для их получения я воспользуюсь методом средневзвешенного значения Оно рассчитывается следующим образом 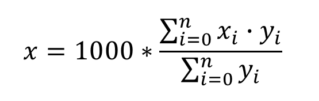 Для нашего примера мы получим следующее 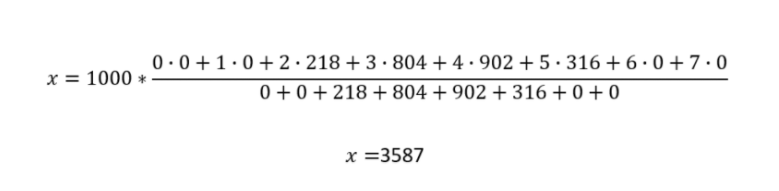 Эта формула будем возвращать нам значение от 0 до 7000, где 0 означает, что датчик находится в крайнем левом углу, а 7000 означает, что он находится справа. А полученное нами ранее значение 3587 говорит о том, что мы находимся на черной линии. Итак, самое время применить ПИД-регулятор, для управления роботом 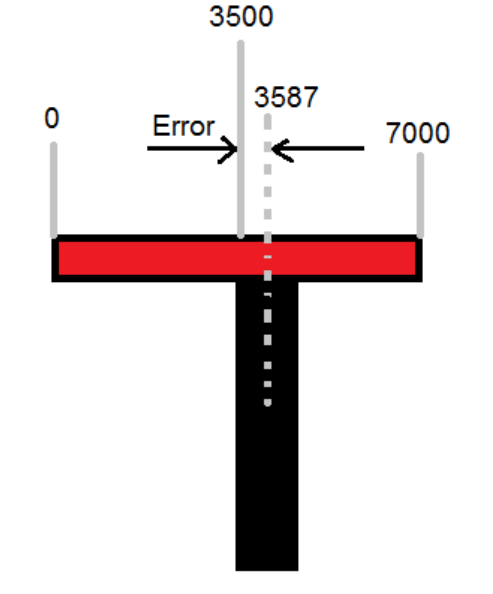 Идеальным для нас положением будет значение в 3500. Назовем его SetPoint. Как мы говорили ранее ошибкой будет разница между текущей позиции и заданного значения Ошибка = 3587 – 3500 = 87 Итак, формула ПИД-регулятора: 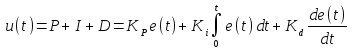 u (t) — наша Функция; P — пропорциональная составляющая; I — интегральная составляющая; D — дифференциальная составляющая; e (t) – текущая ошибка; Kp — пропорциональный коэффициент; Ki — интегральный коэффициент; Kd — дифференциальный коэффициент; У нас есть воздействие, наша Функция (u (t) ). Она состоит из трех составляющих – Пропорциональной, Интегральной и Дифференциальной (отсюда и ПИД-регулятор). Формула в вышеприведенном виде хороша для изучения, но неудобна для расчетов (хотя бы потому, что в вычислительной технике надо переходить к численным методам). В программной реализации, переходят к дискретной реализации: u(t) = P (t) + I (t) + D (t); P (t) = Kp * e (t); I (t) = I (t — 1) + Ki * e (t); D (t) = Kd * {e (t) — e (t — 1)}; Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую. Впрочем, есть еще и другая, рекуррентная реализация: u(t) = u(t — 1) + P (t) + I (t) + D (t); P (t) = Kp * {e (t) — e (t — 1)}; I (t) = I * e (t); D (t) = Kd * {e (t) — 2 * e (t — 1) + e (t — 2)}; Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже. Говорят, что есть разные подводные булыжники при реализации. Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double. Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце. А сейчас переведем дух от математики и поедем к изучению поведения этой формулы. Я построил несколько графиков в Excel по нашим показаниям и рассчитал каждую составляющую Пропорциональная составляющая Первый коэффициент – пропорциональный. Он самый очевидный и понятный. Рассмотрим его – пропорционального коэффициента — влияние на результат. 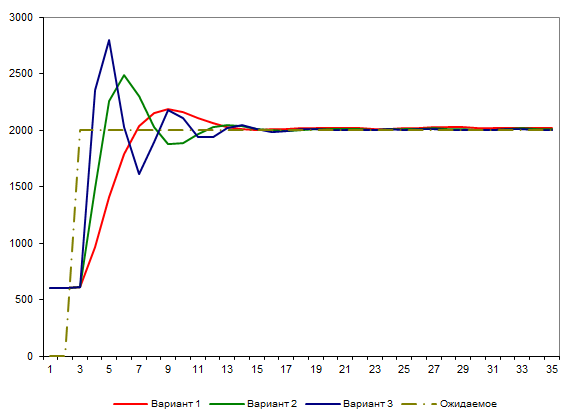 «Ожидаемое» – это то, что мы хотим получить. Вначале оно равно какому-то низкому значению (в нашем примере – это те показания датчика, которые мы считываем). Сделаем первый вариант: Kp = 2. Посмотрим на красную линию. Что мы видим? По ходу дела показания начали расти – ошибка стала снижаться – значение коррекции постепенно растет — красная линия растет. В какой-то момент показания датчиков достигают требуемой величины. Класс? Супер! Да вот только медленно как-то… Попробуем другой коэффициент: Kp = 5. Что видим? Зеленая линия. Достигла результата шустро – на 6-ом шаге. Класс! Да вот – ой! – перелет (перерегулирование). Потом, правда, вернулись назад – порядок. А что если коэффициент сделать еще больше? Kp = 20. Синяя линия – бух! За один шаг! Но – сразу перелет. Потом падаем вниз – ошибка стала отрицательной. Опять сильно вниз! Рывок вверх! Опять вниз! Что видим? Пошли колебания. Они затухающие. Если увеличивать коэффициент больше, то такие колебания могут стать незатухающими. Система начнет колебаться все больше и больше, пока не … ну-у, тут уже все зависит от конкретной системы. Какова природа колебаний? Система, на которую воздействуют, всегда (в реальной жизни) инерционна. Обороты повышаются – коэффициент падает к нулю. И вот – достигли нужной точки. Коэффициент ошибки (и регулирования) достиг нуля. Но ведь процесс поднятия оборотов инерционен! Для решения этой проблемы используется следующая – Интегральная составляющая Эта составляющая накапливает ошибку (как и любой интегратор). Т. е. постепенно накапливается эта самая ошибка, интегратор «наполняется» и его воздействие увеличивается. Эффект от такого накопления не мгновенен — ибо ошибка должна накопиться, на что уходит некоторое количество шагов алгоритма. Рассмотрим случай, когда Kp = 5, а Ki будем менять: 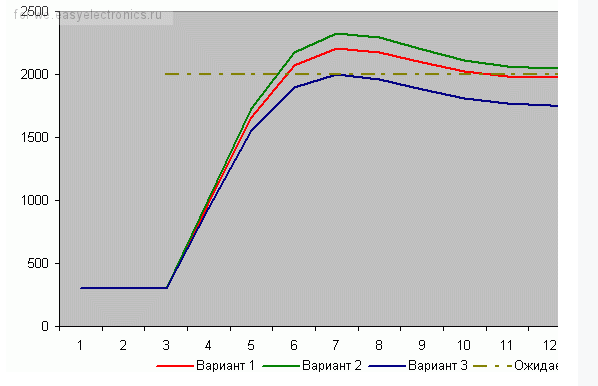 Вариант 1 (красный) – Ki = 0. Вариант 2 (зеленый) – Ki = 0.2. Вариант 3 (синий) – Ki = -0.3. Использование положительного коэффициента (зеленая линия) в данном случае, пожалуй, ничего нам не дало. А вот отрицательный коэффициент (синяя линия) очень даже неплохо помог! Но вот только линяя пошла вниз, и потом она приведет к раскачиванию системы… (но на практике раскачивания системы, как правило, не происходит, т. к. постоянно будут коррекции текущего состояния) Итак, интегральная составляющая позволила нам сгладить резкий эффект пропорциональной составляющей. Это неплохо! Но вы погодите – сейчас нам покажет всю свою мощь Дифференциальная составляющая Эта составляющая пропорциональна темпу изменений. Она «придает ускорение». Как и ранее, Kp = 5, а Kd будем менять: 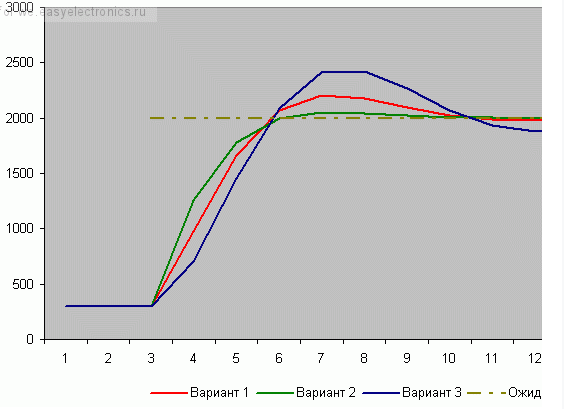 Вариант 1 (красный) – Kd = 0. Вариант 2 (зеленый) – Kd = 0.2. Вариант 3 (синий) – Kd = -0.2. Каково? И сглаживает, и не дает раскачиваться в будущем! Настройка пропорционального коэффициента Kp Для начала я устанавливаю коэффициент Kp в 1 и смотрю, что будет. Растет слишком медленно – увеличиваю. В какой-то момент начнутся перелеты и колебания. Значит, многовато – уменьшаем. Исчезли – немного увеличиваем. Начались – немного уменьшаем. Исчезли — … И так далее, пока не надоест. В итоге получили достаточно устойчивый пропорциональный регулятор, который надо немного скорректировать (надо ли?Если все работает вполне качественно, то не морочим себе голову и считаем, что все настроено) Настройка дифференциального коэффициента Kd Понемногу наращиваю коэффициент Kd — 0.5, 1,… Колебания системы уменьшаются, все работает красивее… Пока не происходит обратное – начинаются мощные выбросы. Все, перерегулировали, уменьшаем. Итак, имеем выбросы – уже меньше, но все равно имеем. Самое то сгладить, притормозить воздействие! Настройка интегрально го коэффициента Ki Шаманим дальше. Берем совсем немного – 0.1 для начала. Можно попробовать и небольшое отрицательное значение. Смотрим, пробуем, крутим… Процесс этот – настройки – итерационный. Стоит пробовать разные варианты, начинать сначала. |
