ПРАКТИКА ФТТ БА 1 (1). Пространственная решетка и ее свойства
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
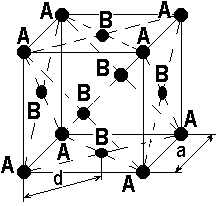
ФИЗИКА ТВЕРДОГО ТЕЛА Оглавление Введение 3 1. Пространственная решетка и ее свойства 5 1.1. Элементарные ячейки и структура кристаллов 5 Задачи для самостоятельных и домашних работ 11 1.2. Плоскости в кристаллической решетке. Индексы Миллера 13 Задачи для самостоятельных и домашних работ 17 1.3. Обратная решетка и ее свойства. 18 Задачи для самостоятельных и домашних работ 23 Дифракция рентгеновских лучей в кристаллах. Формула Вульфа-Брэгга. 23 Задачи для самостоятельных и домашних работ 27 3. Межатомные взаимодействия и типы связей в твердых телах 29 Задачи для самостоятельных и домашних работ 34 4. Дефекты в кристаллах, диффузия. 37 Задачи для самостоятельных и домашних работ. 41 5. Динамика кристаллической решетки. 43 Пространственная решетка и ее свойства 7. Элементарные ячейки и структура кристаллов Задача 1. Плотность кристалла NaC1 равна 2180 кг/м3. Атомный вес натрия 23, хлора 35,46. Определить постоянную решетки. Решение. Масса элементарной ячейки кристалла NaCl равна M=a3 где a – постоянная решетки, – плотность кристалла. Но, с другой стороны, = mH (NNaANa + NClACl) где mH – масса атома водорода (1,6610-27 кг); NNa – число атомов натрия в элементарной ячейке; NCl – число атомов хлора в элементарной ячейке; ANa – атомный вес натрия; ACl –атомный вес хлора. Приравнивая правые части двух выражений и учитывая, что на одну элементарную ячейку NaC1 приходится половина атома натрия и половина атома хлора, получаем 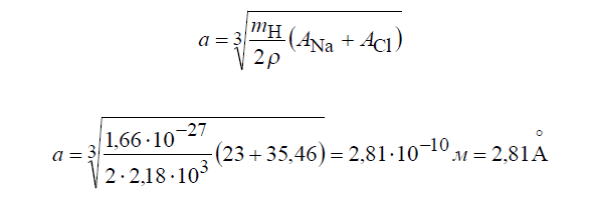 Задача 2. Найти число атомов алюминия в единице объема. Плотность алюминия =2700 кг/м3. Решение. В килограмм-молекуле алюминия содержится 6,021026 атомов. Одна килограмм-молекула занимает объем: V1=A/ где A – атомный вес, – плотность . Тогда число атомов в единице объема: 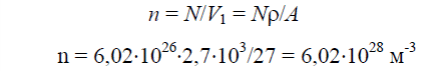 Задача 4 (6). Определить объемы элементарной ячейки через радиусы равновеликих шаров, образующих плотные упаковки для 1) объемно- центрированной, 2) гранецентрированной и 3) гексагональной решеток. Решение. 1) Параметр элементарной ячейки через радиус шара выражается следующим образом (рис. 2):  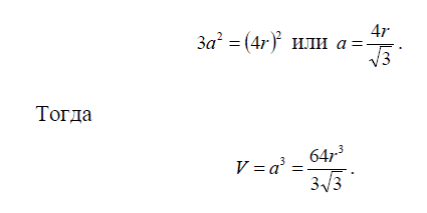  Задача 5 (7). Чему равно число атомов в элементарной ячейке в случае 1) простой, 2) объемноцентрированной и 3) гранецентрированной кубических решеток? Решение. 1) В простой кубической решетке атомы находятся только в вершинах углов ячейки. Одна вершина принадлежит восьми параллелепипедам кристаллической решетки. Поэтому на каждую вершину одной ячейки приходится одна восьмая часть атома, находящегося в вершине (рис. 4а). 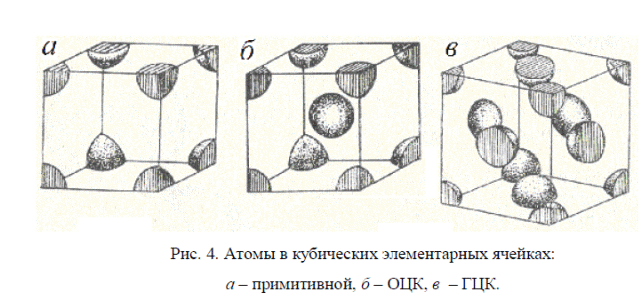 Ячейка имеет восемь углов, следовательно, на нее приходится один атом. 2) В объемноцентрированной кубической решетке, кроме атомов, расположенных в углах, элементарной ячейке принадлежит полностью внутренний центральный атом (рис. 4б). Таким образом, в объемно- центрированной решетке на каждую ячейку приходится два атома. 3) В гранецентрированной кубической решетке атомы, расположенные в центре граней, принадлежат двум ячейкам (рис. 4в). Поэтому число атомов в элементарной ячейке равно четырем. Задача 6 (8). Чему равно число атомов в элементарной ячейке гексагональной плотноупакованной решетки? Решение. На элементарную ячейку в гексагональной плотноупакованной решетке приходится шесть атомов. Три внутренних атома, которые расположены в центрах трех (из шести) тригональных призм (рис. 5), полностью принадлежат одной элементарной ячейке.  Два атома, расположенные в центрах базисных граней, принадлежат элементарной ячейке наполовину и в сумме дают один атом. Каждый атом, который находится в вершине гексагональной призмы, принадлежит шести элементарным ячейкам. В целом все эти двенадцать атомов вносят вклад в одну элементарную ячейку на два атома. Итак, на элементарную ячейку гексагональной решетки приходится шесть атомов.  Задача 8 (12). Пусть гранецентрированная кубическая и гексагональная решетки построены из одинаковых атомов, представляющих собой жесткие сферы с радиусом r. Показать, что часть объема, занятая атомами при таком расположении, равна Решение. Для гранецентрированной кубической решетки N=4, объем элементарной ячейки равен Тогда 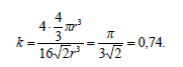 Поскольку в элементарной ячейке гексагональной решетки содержится шесть атомов, то коэффициент заполнения пространства определяется выражением 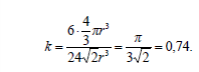 Таким образом, в гексагональной решетке, равно как и в гранецентрированной кубической, атомами заполнено всего лишь 74% пространства от общего объема решетки. Из приведенных вычислений следует, что даже в решетках с самой плотной упаковкой атомов остаются незаполненными 26% пространства от общего объема решетки. Задача 9 (22). Вычислить объем элементарной ячейки триаминхлорида четырехвалентной платины, если параметры ячейки и углы триклинности  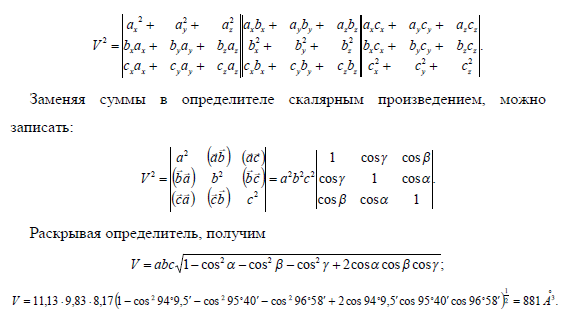 Задача 10 (23). Воспользовавшись формулой объема элементарной ячейки триклинной системы, получить формулы для объема ячеек 1) моноклинной, 2) гексагональной и 3) ромбоэдрической систем.     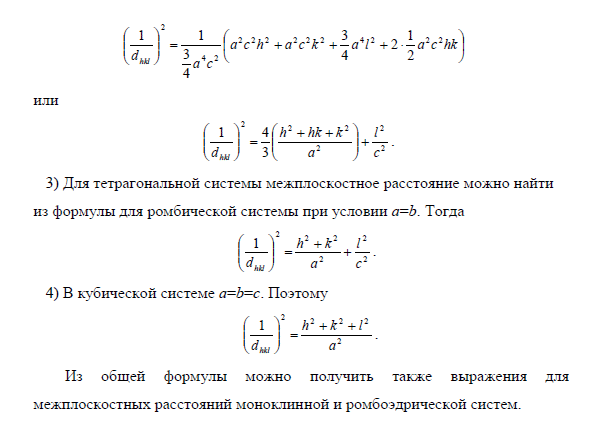 Механические свойства твёрдых тел Задача 1Оценить постоянную решетки |
| | (3.1) |
В соответствии с законом Гука для однородного стержня такая деформация наблюдается при приложении к концам стержня растягивающего усилия с нормальным напряжением
| | (3.2) |
где Е – модуль Юнга материала стержня.
Из формул (3.1) и (3.2) следует, что для предотвращения теплового расширения стержня к его концам необходимо приложить сжимающее усилие с нормальным напряжением
| | (3.3) |
Ответ:
Таблица 1 – Варианты заданий для решения Пример№1
| Вариант | | ∆Т=1К | Е=6,9 |
| 1 | 2,8 | 2 | = |
| 2 | 2,9 | 4 | = |
| 3 | 3 | 6 | = |
| 4 | 2,5 | 8 | = |
| 5 | 2,4 | 10 | = |
| 6 | 2,8 | 1 | = |
| 7 | 2,8 | 12 | = |
| 8 | 2,9 | 2 | = |
| 9 | 3 | 4 | = |
| 10 | 2,5 | 6 | = |
| 11 | 2,4 | 8 | = |
| 12 | 2,8 | 10 | = |
| 13 | 2,8 | 1 | = |
| 14 | 2,9 | 12 | = |
Вопросы к практическому занятию:
Напишите конспективно ответы на вопросы:
Вопрос 1. Какие бывают деформации?
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Вопрос 3. Как направлена сила упругости?
Вопрос 4. Какую природу имеет сила упругости?
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?

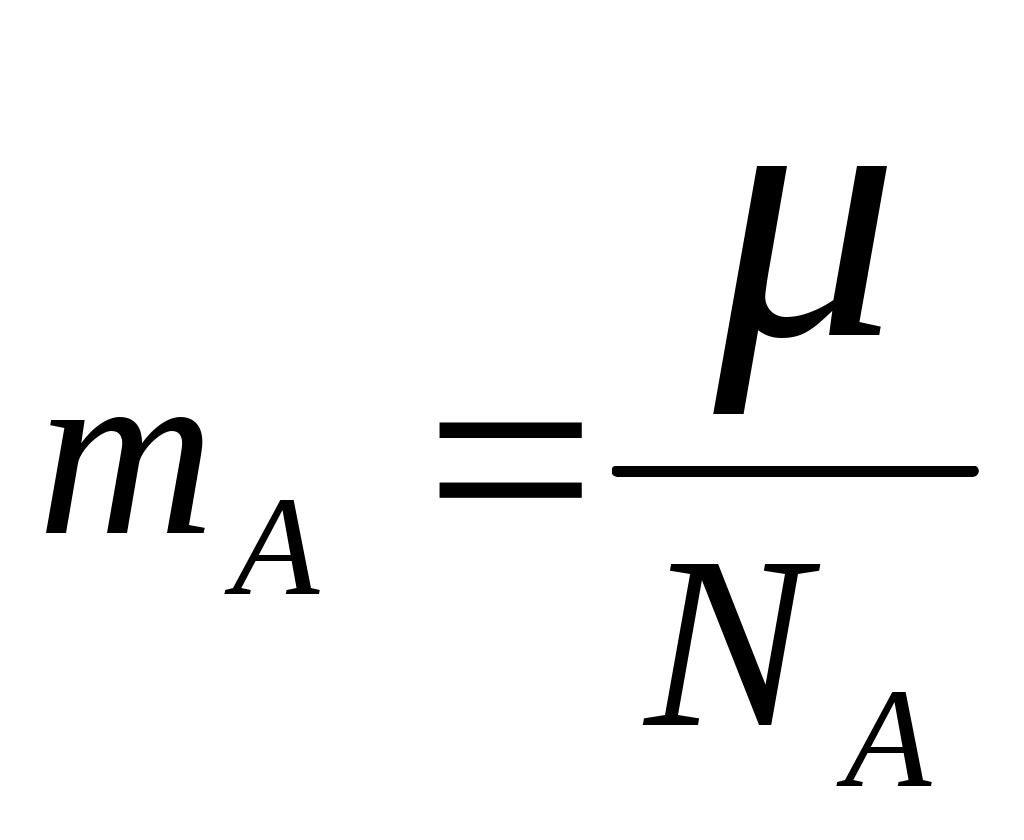 , где NA - число Авогадро.
, где NA - число Авогадро.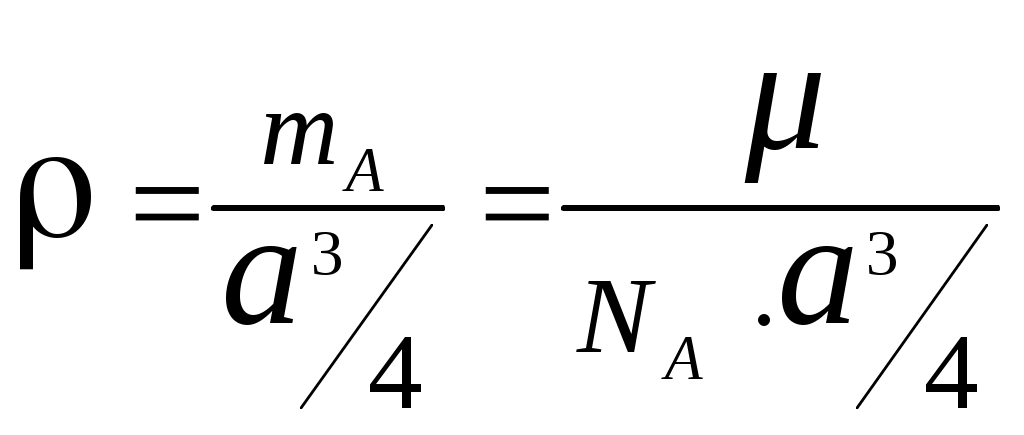 ,
,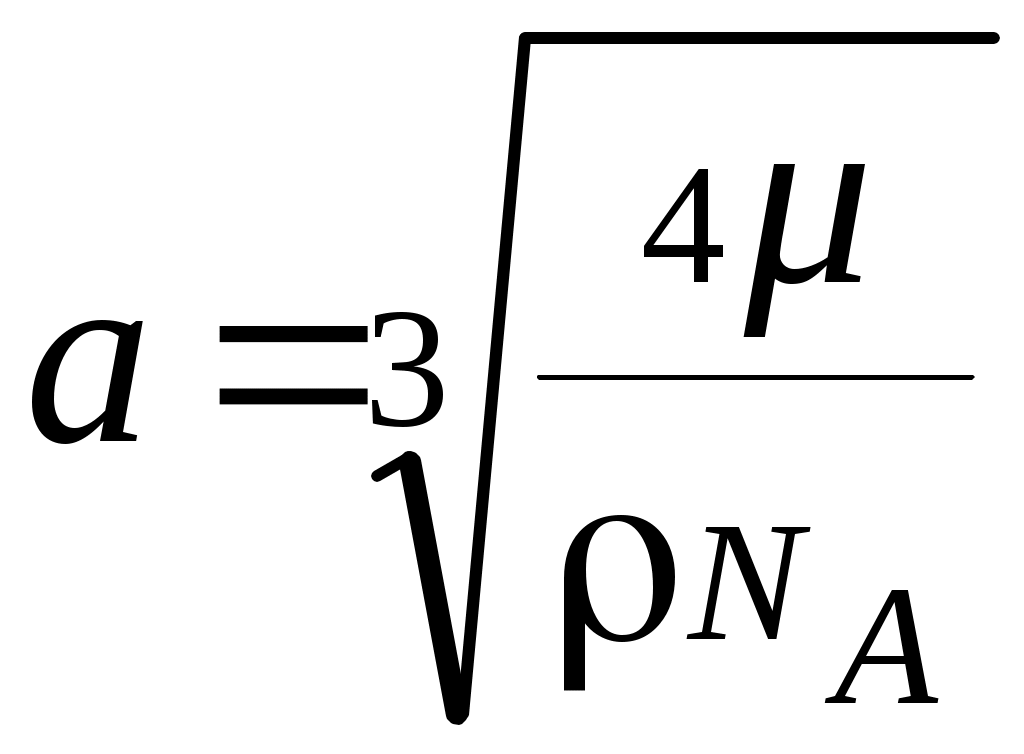 , или
, или 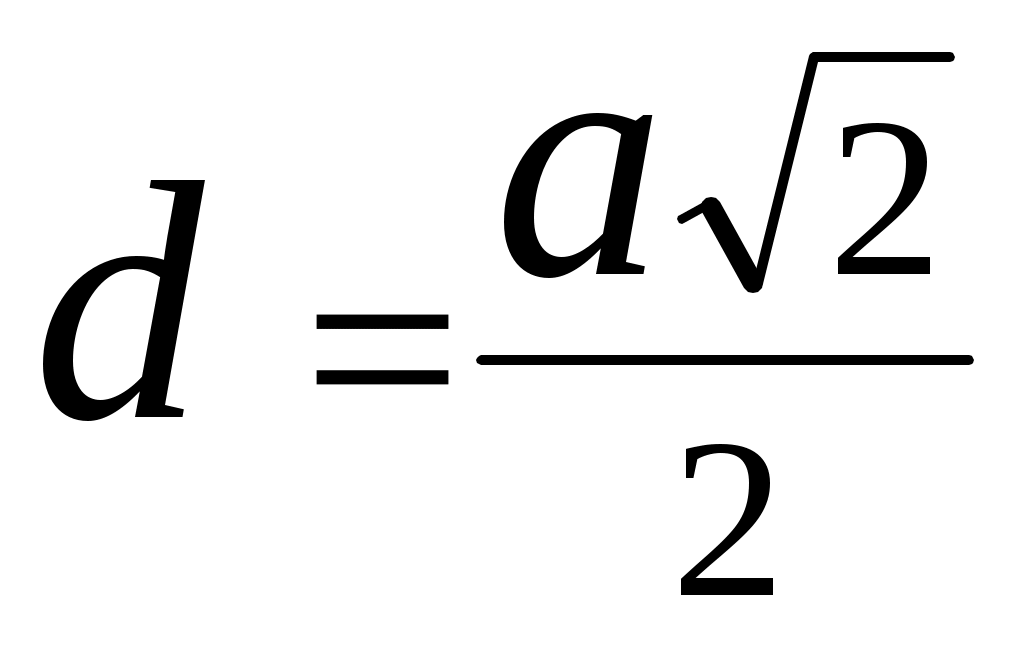 , отсюда
, отсюда 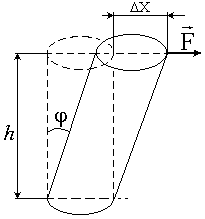 равните величину относительной деформации φ (угол сдвига) и смещения верхнего основания двух цилиндров одинаковых размеров, сделанных один из чугуна, а другой из свинца, если на верхнее основание каждого (вдоль него) действует одна и та же сила, а нижние основания закреплены. Какой из этих материалов вы бы предпочли для изготовления болтов?
равните величину относительной деформации φ (угол сдвига) и смещения верхнего основания двух цилиндров одинаковых размеров, сделанных один из чугуна, а другой из свинца, если на верхнее основание каждого (вдоль него) действует одна и та же сила, а нижние основания закреплены. Какой из этих материалов вы бы предпочли для изготовления болтов?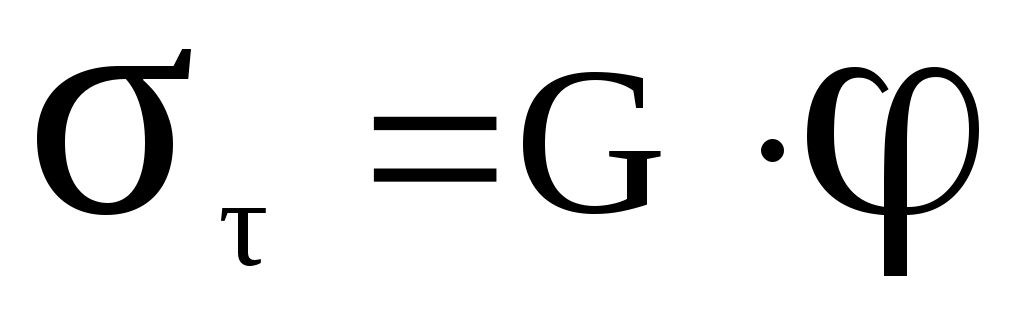 , (3)
, (3)
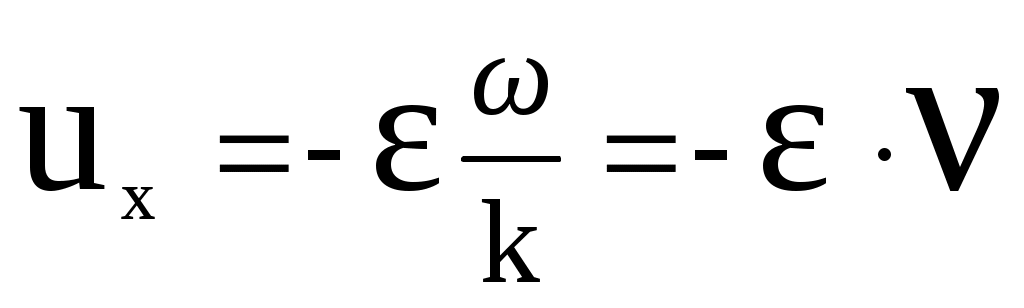 .
.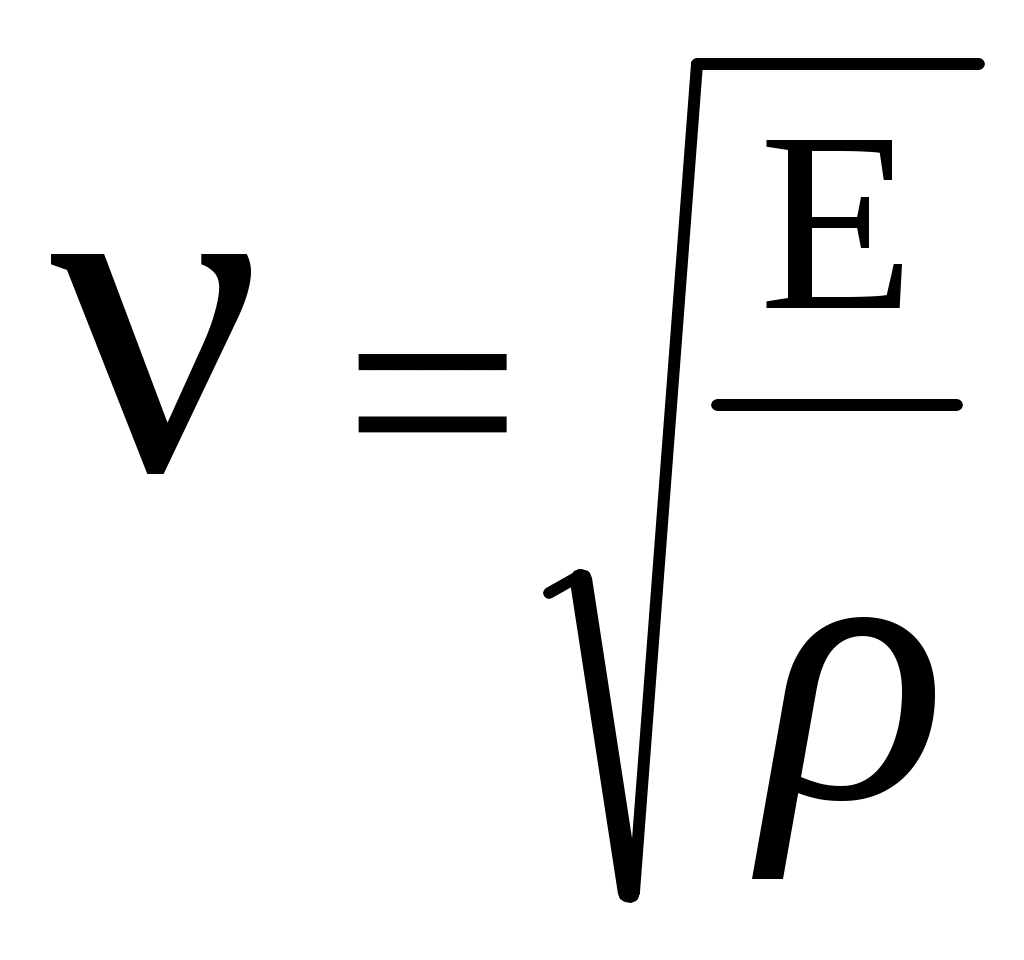 ,
,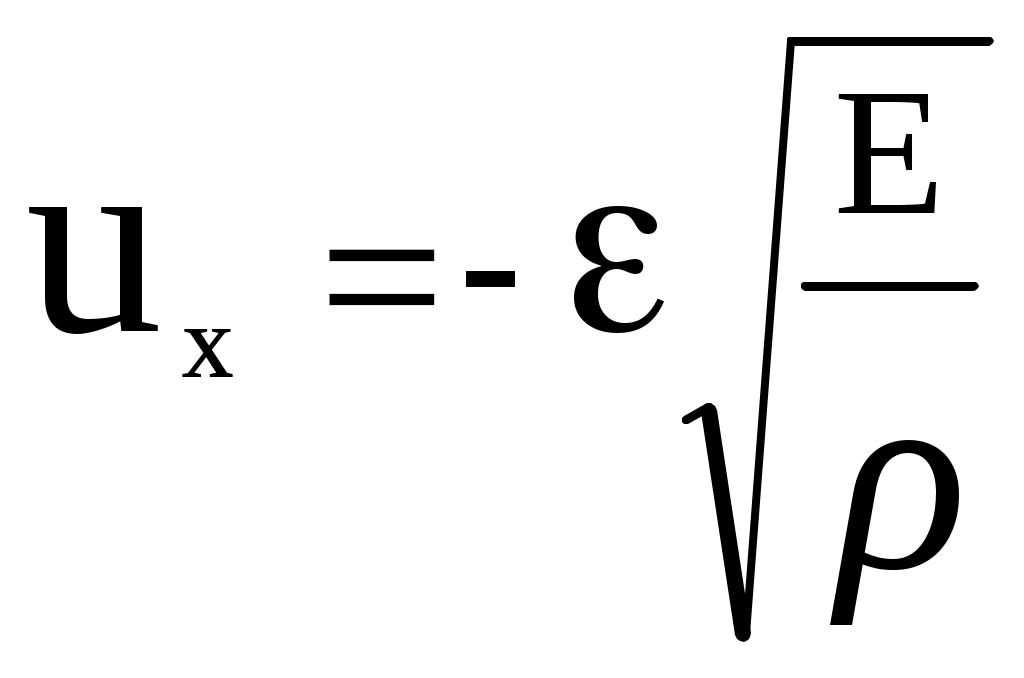 .
.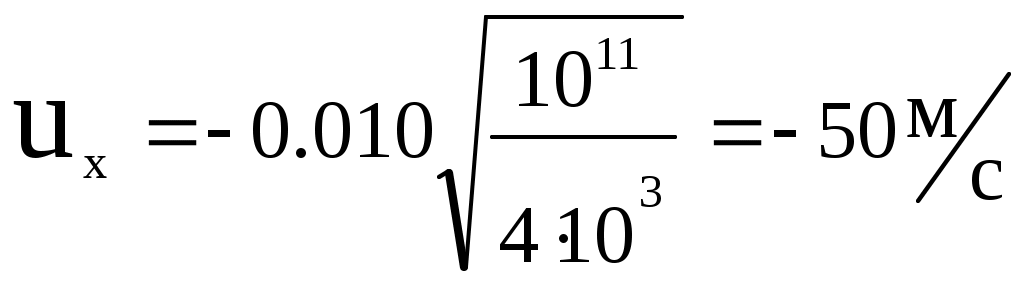 .
.