Закон Гука при чистом сдвиге ( ) действует на участке диаграммы Ответ 01
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
|
№1. Закон Гука при чистом сдвиге ( 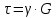 ) действует на участке диаграммы: ) действует на участке диаграммы: 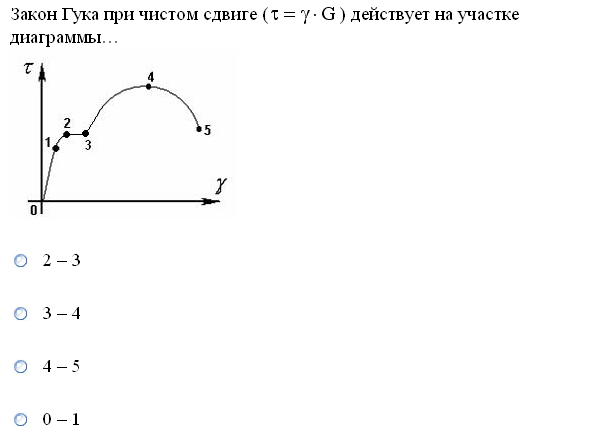 Ответ: 0-1. Ответ: 0-1.№2. Если предел пропорциональности материала и соответствующая ему деформация равны 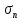 = 100 МПа, = 100 МПа, 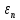 = 0,0014, тогда величина модуля упругости равна: 71429 МПа. = 0,0014, тогда величина модуля упругости равна: 71429 МПа.№3. При испытаниях образца на растяжение были определены продольная и поперечная относительные деформации. Они оказались равными 0,00032 и 0,00013. Тогда величина коэффициента Пуассона равна: 0,4. №4. Свойство твердых тел сохранять остаточную деформацию называется: пластичностью. №5. Суммарный момент относительно оси стержня всех внутренних сил, действующих в поперечном сечении, называется: крутящим моментом. №6. Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут: растягивающими.  №7. Для стержня, схема которого изображена на рисунке, нормальное усилие N в сечении 1-1 будет: равны нулю.  №8. Для стержня, схема которого изображена на рисунке, нормальное усилие N в сечении 1-1 будет: сжимающим. 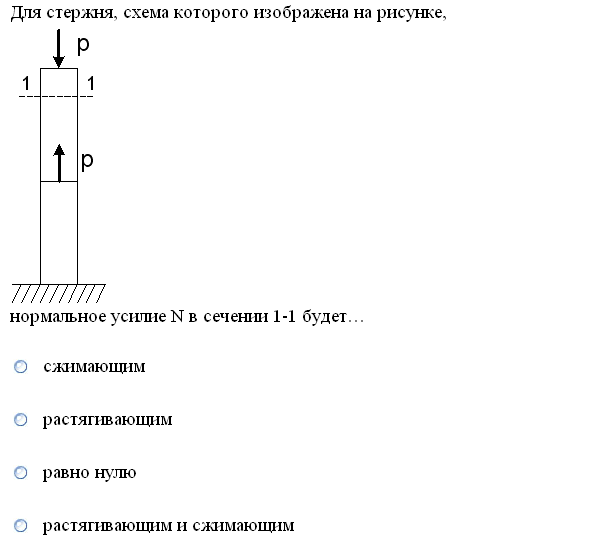 №9. Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут: растягивающими. 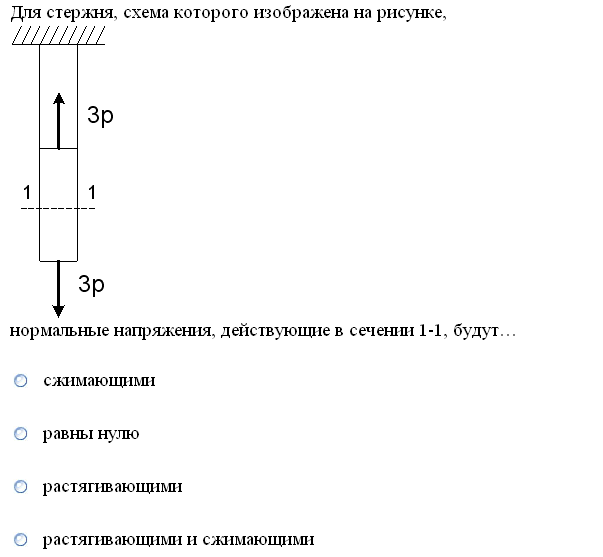 №10. Для стержня, схема которого изображена на рисунке, нормальное усилие N в сечении 1-1 будет: равны нулю.  №11. Закон Гука при чистом сдвиге выражается формулой: 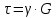 . .№12. Площадь поперечного сечения тела заклепки – А. Касательные напряжения в поперечном сечении, в месте среза, определяются по формуле: 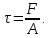  №13. В точке 1 поперечного сечения А-А балки: нет напряжений. 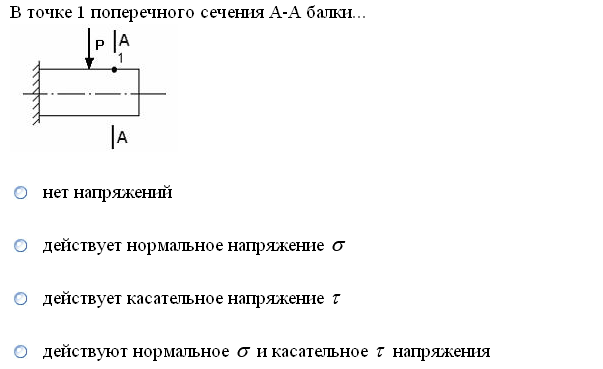 №14. В точке 1 поперечного сечения А-А балки: нет напряжений.  №15. В точке 1 поперечного сечения А-А балки:Действует нормальное и касательное напряжение. 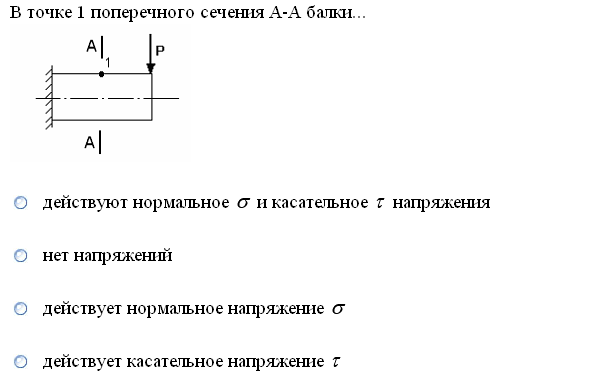 №16. В сечении 1-1 имеют место внутренние силовые факторы: М ≠ 0 Q ≠ 0. 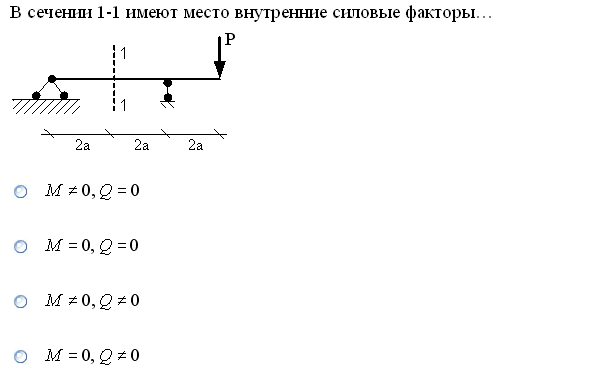 №17. В сечении 1-1 имеют место внутренние силовые факторы: М ≠ 0 Q ≠ 0. 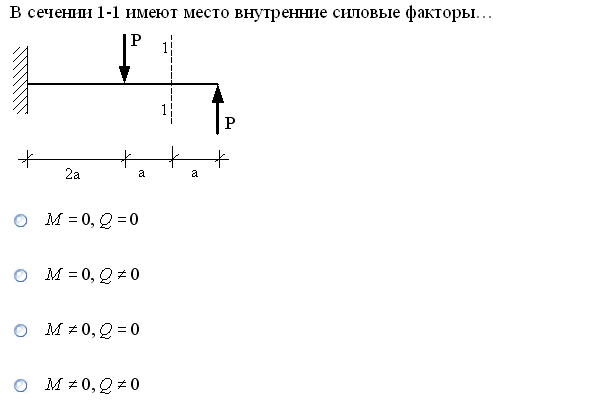 №18. Максимальный прогиб возникает в сечении: 4-4.  №19. Максимальный угол поворота возникает в сечении: 1-1.  №20. Для нагруженного стержня вид сложного сопротивления называется: Общим случаем сложного сопротивления. 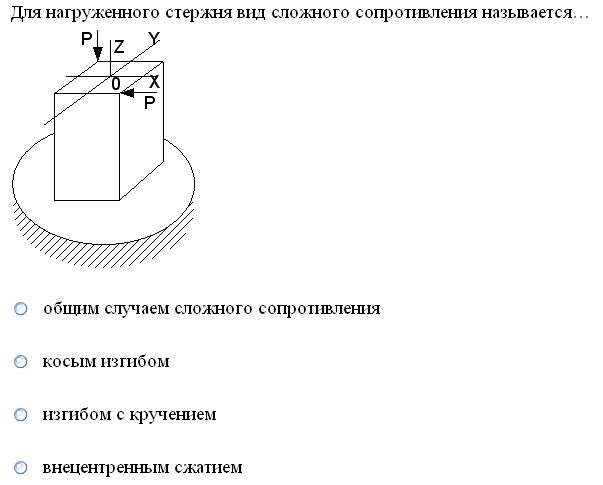 №21. Для нагруженного стержня вид сложного сопротивления называется: Общим случаем сложного сопротивления. 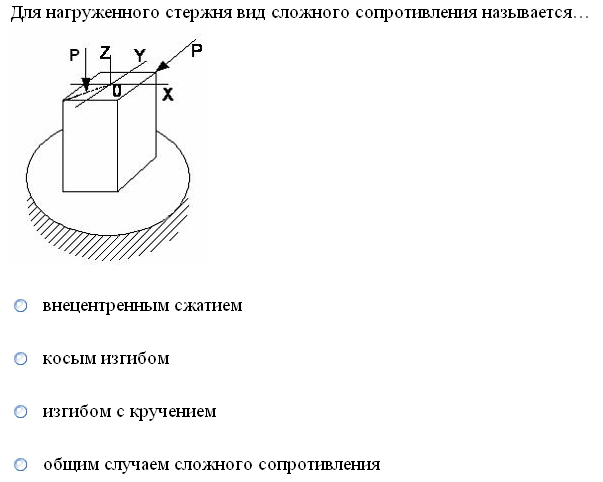 №22. Для нагруженного стержня вид сложного сопротивления называется: Косым изгибом. 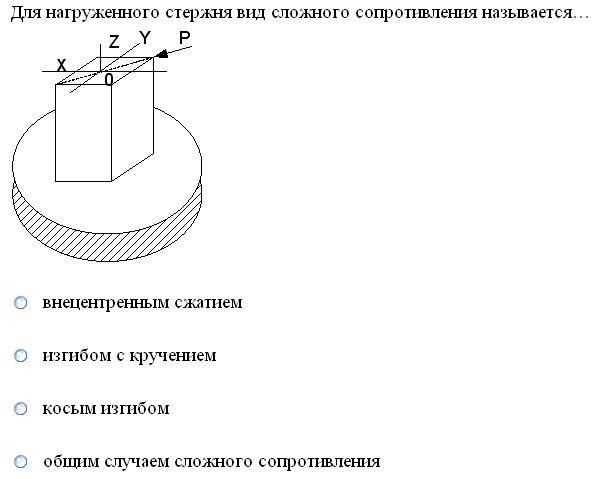 №23. Для нагруженного стержня вид сложного сопротивления называется: Внецентренним растяжением. 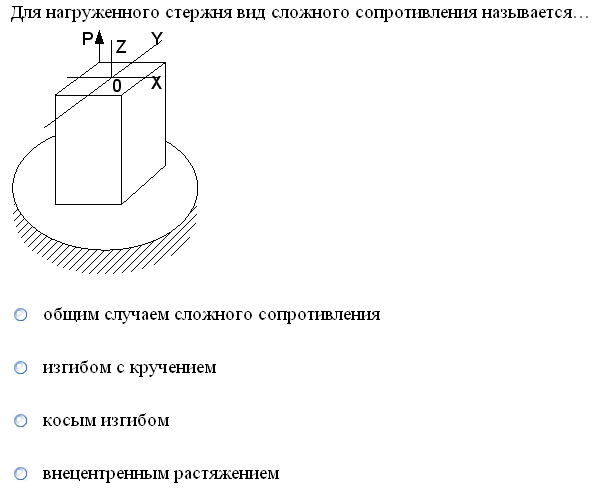 №24. На схеме, изображенной на рисунке, наиболее опасной точкой является: Точка 1. 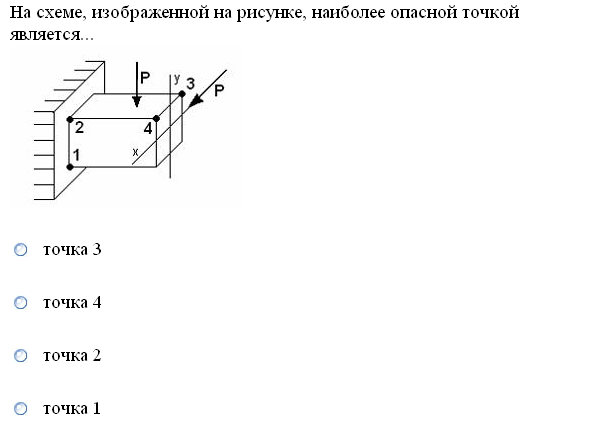 №25. В сечении А-А наиболее опасными являются точки: 1 и 3. 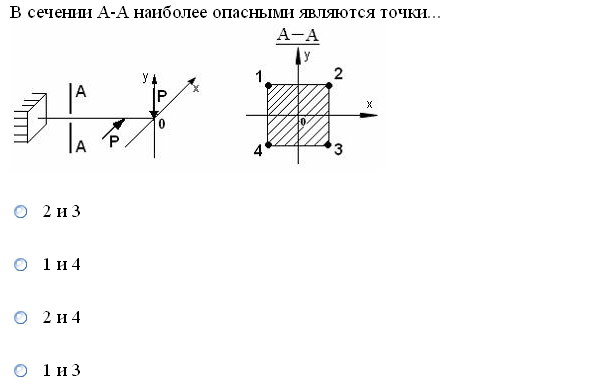 №26. На схеме, изображенной на рисунке, наиболее опасной точкой является: точка 2. 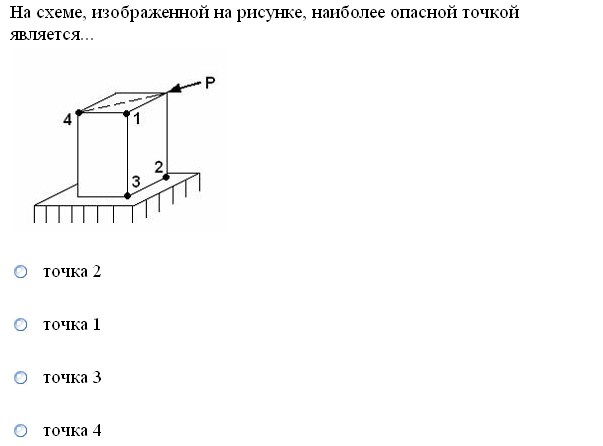 №27. Опасными точками являются точки: А и С. 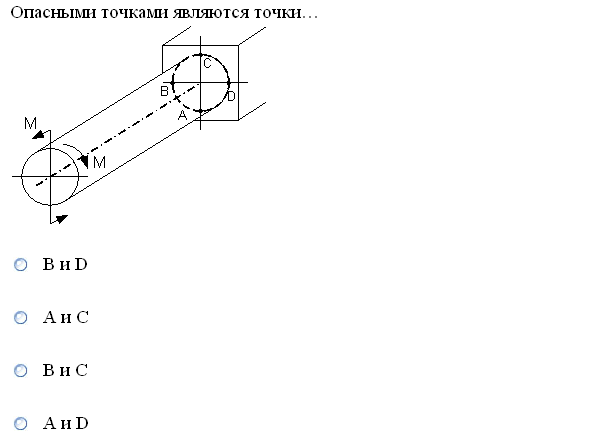 №28. Эпюра изгибающего момента имеет вид: 3. 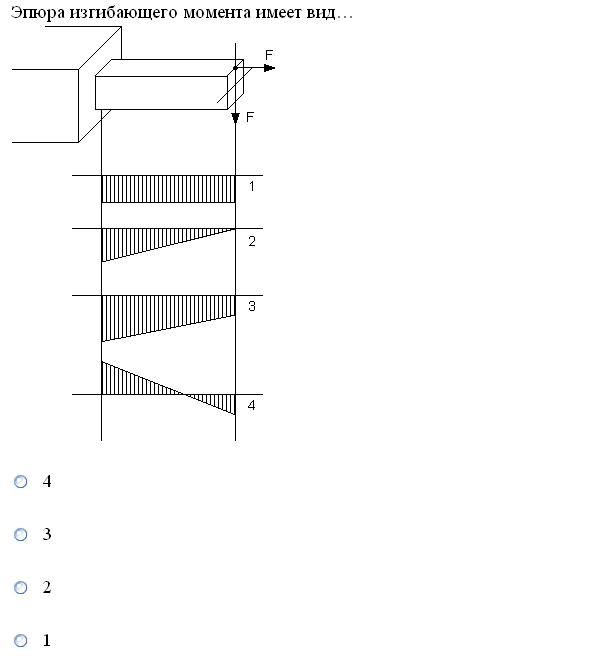  №29. Опасными точками являются точки: В и Д. 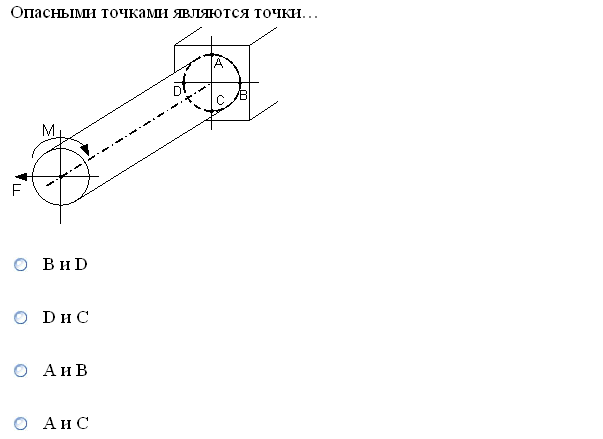 №30. В сечении 1-1 крутящий момент по модулю равен: 2М. 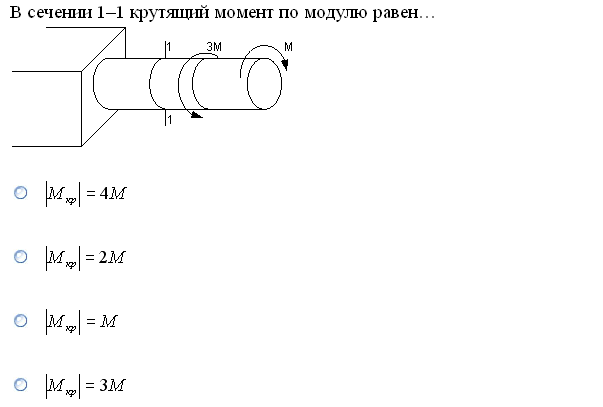 №31. Максимальный относительный угол закручивания имеет место на участке: III. 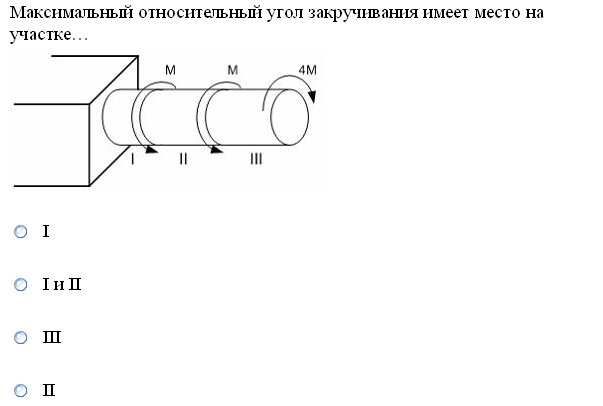 №32. Касательное напряжение в центре тяжести поперечного сечения (точка К) равно: равны нулю.  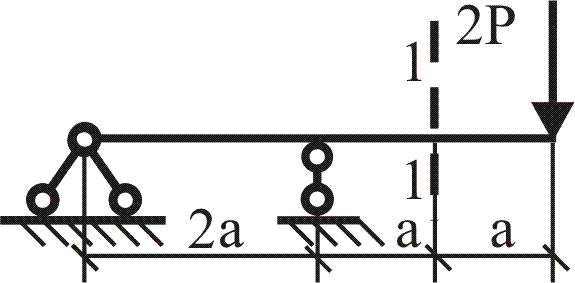 №33. В сечении 1 — 1 имеют место внутренние силовые факторы: №33. В сечении 1 — 1 имеют место внутренние силовые факторы:  . .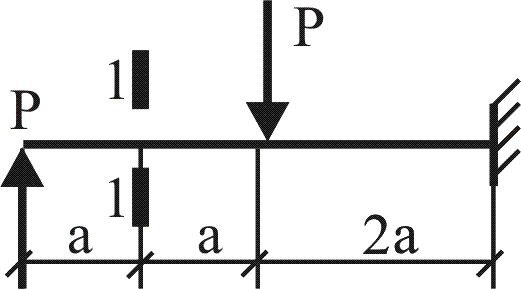 №34. В сечении 1 — 1 имеют место внутренние силовые факторы: №34. В сечении 1 — 1 имеют место внутренние силовые факторы:  . .№35. В сечении 1 — 1 имеют место внутренние силовые факторы: 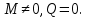  №36. В сечении 1 — 1 имеют место внутренние силовые факторы:  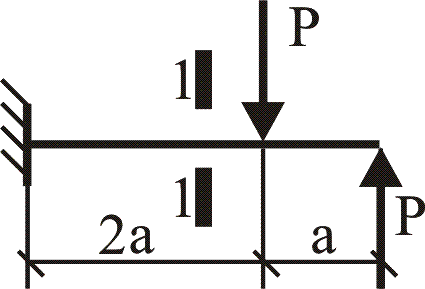 №37. В сечении 1 — 1 имеют место внутренние силовые факторы: 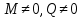 . .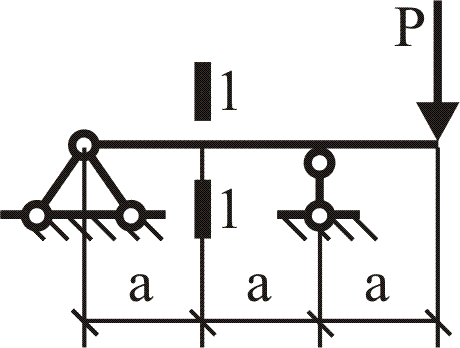  №38. В сечении 1 — 1 имеют место внутренние силовые факторы: №38. В сечении 1 — 1 имеют место внутренние силовые факторы: 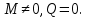 №39. Приведенная на рисунке форма потери устойчивости сжатого стержня соответствует способу закрепления стержня, показанному на схеме: 2.  №40. Шарнирно опертая балка нагружена сосредоточенным моментом М. Допускаемое напряжение для материала балки равно  . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W M/2 M/2 . . №41. Предел выносливости детали при наличии концентрации напряжений: уменьшается. №42. Остаточной (пластической) деформацией называется деформация: не исчезающая после прекращения действия внешних сил. №43. Прочность – способность конструкции и ее элементов: выдерживать приложенные к ним силы, не разрушаясь. №44. Из условия прочности вала при допускаемом напряжении на кручение 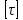 полярный момент сопротивления полярный момент сопротивления 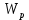 равен: равен: 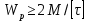 . .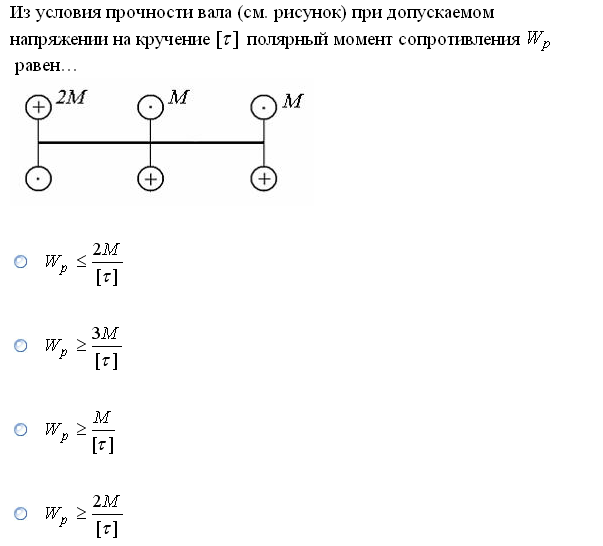 №45. На рисунке показана схема нагружения балки. 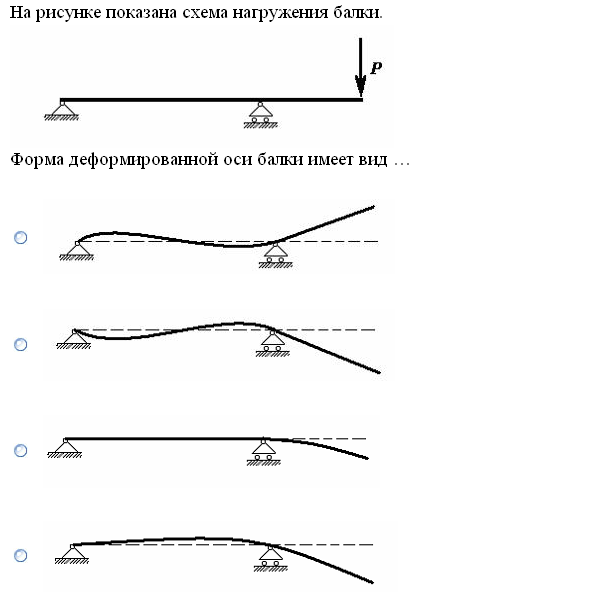 Форма деформированной оси балки имеет вид: №46. Консольная балка нагружена сосредоточенным моментом М. Осевой момент сопротивления поперечного сечения балки равен W. 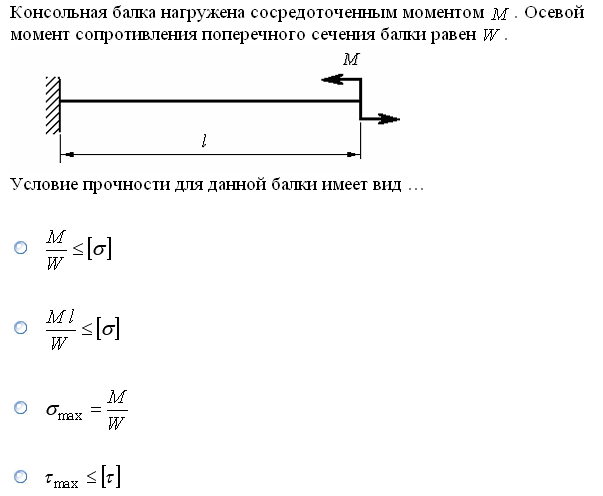 Условие прочности для данной балки имеет вид: M/W  . .№47. Эпюра касательных напряжений в сечении 1-1 имеет вид: 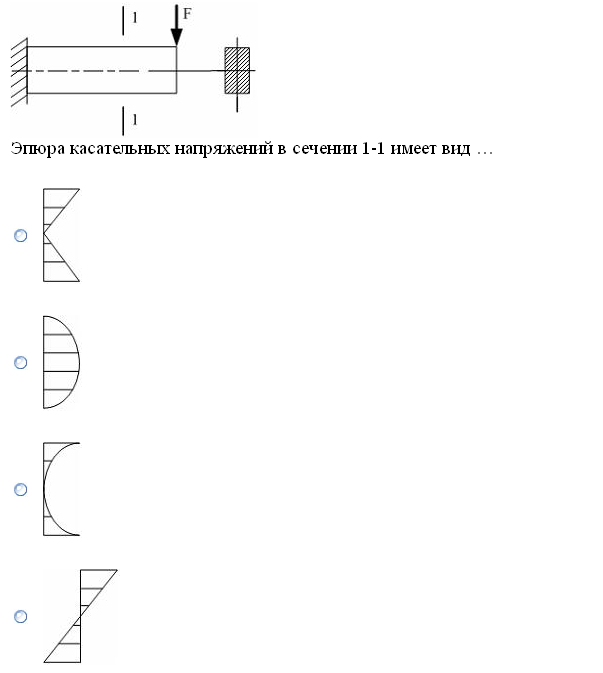 №48. Условие жесткости вала постоянного сечения при допускаемом относительном угле закручивания 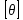 (рад/м) имеет вид: 2M/G (рад/м) имеет вид: 2M/G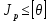 . .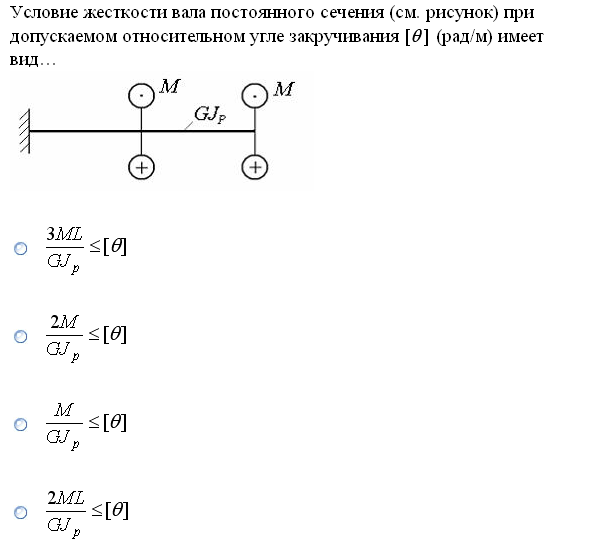 №49. В сопротивлении материалов исследование прочности, жесткости или устойчивости любой конструкции начинается: с выбора соответствующей расчетной схемы. №50. На рисунке показана форма деформированной оси балки: Схема нагружения балки, соответствующая приведенной форме, имеет вид: 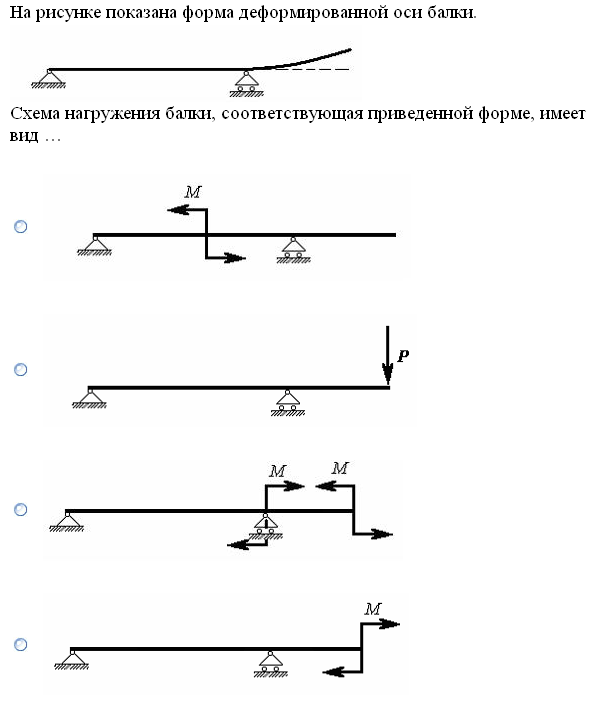 №51. Устойчивостью называется способность элементов конструкции: сохранять под нагрузкой первоначальную форму упругого равновесия. №52. Шарнирно опертая балка нагружена распределенной нагрузкой q.  Эпюра изгибающих моментов для этой балки имеет вид (эпюра строится на сжатых волокнах): №53.  — площадь поперечного сечения тела заклёпки, — площадь поперечного сечения тела заклёпки,  — допускаемое напряжение на срез. Допускаемое значение силы — допускаемое напряжение на срез. Допускаемое значение силы  находится по формуле... находится по формуле...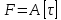 . . №54. Закон Гука при чистом сдвиге ( 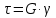 ) действует на участке диаграммы ...0-1. ) действует на участке диаграммы ...0-1.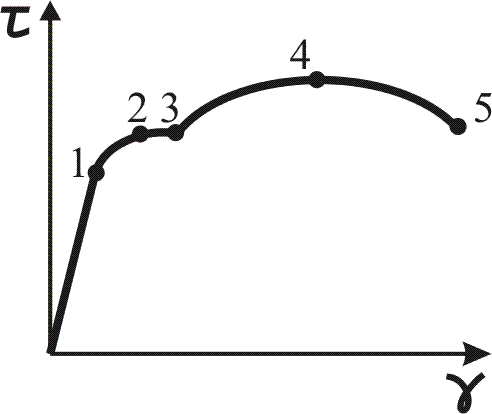 №55. По какой из формул следует рассчитывать устойчивость стержня на участке 2. 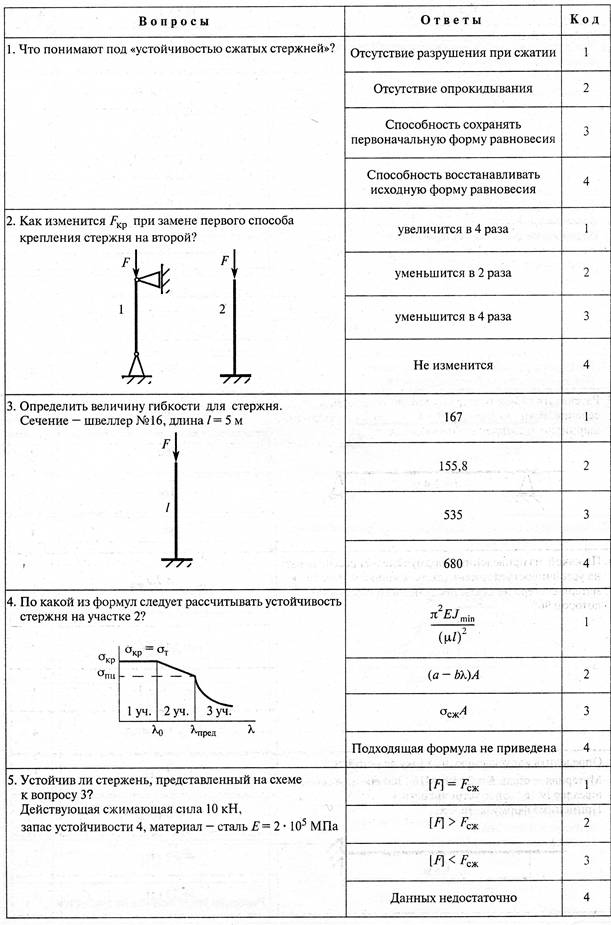 Ответ: (a – b Ответ: (a – b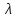 )A. )A.№56. Выбрать правильную запись условия устойчивости: 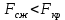 . .№57.Из приведенных характеристик выбрать характеристику, используемую при расчете на устойчивость: 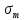 . .№58. Какие напряжения возникают в поперечном сечении бруса при действии сил 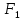 и и 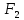 ? ? 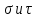 . .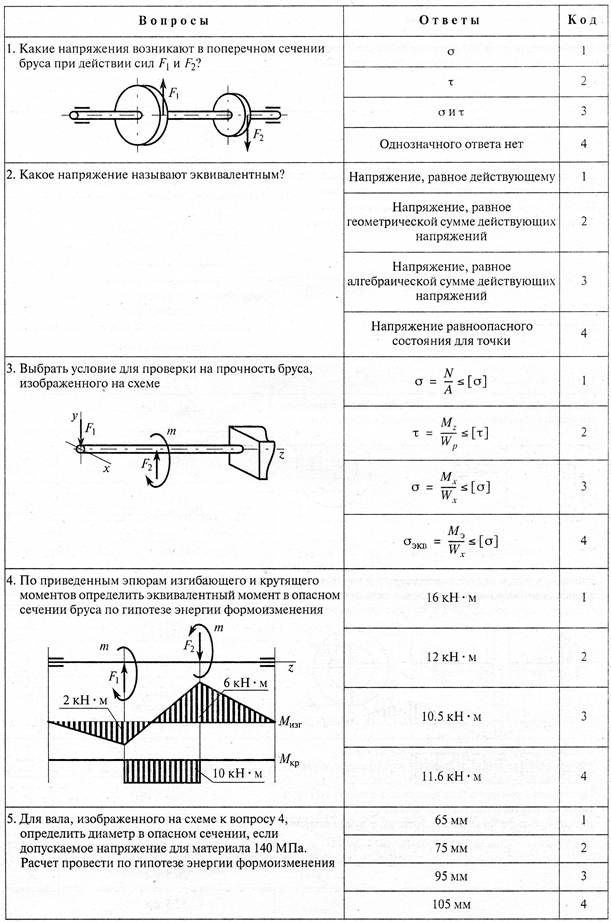 №59. Определить поперечную силу в любом сечении на II участке бруса: -20.  №60. Вычислить величину изгибающего момента в сечении С: -2 кН∙м.  №61. Определить реакцию в опоре В: 18,75 кН. 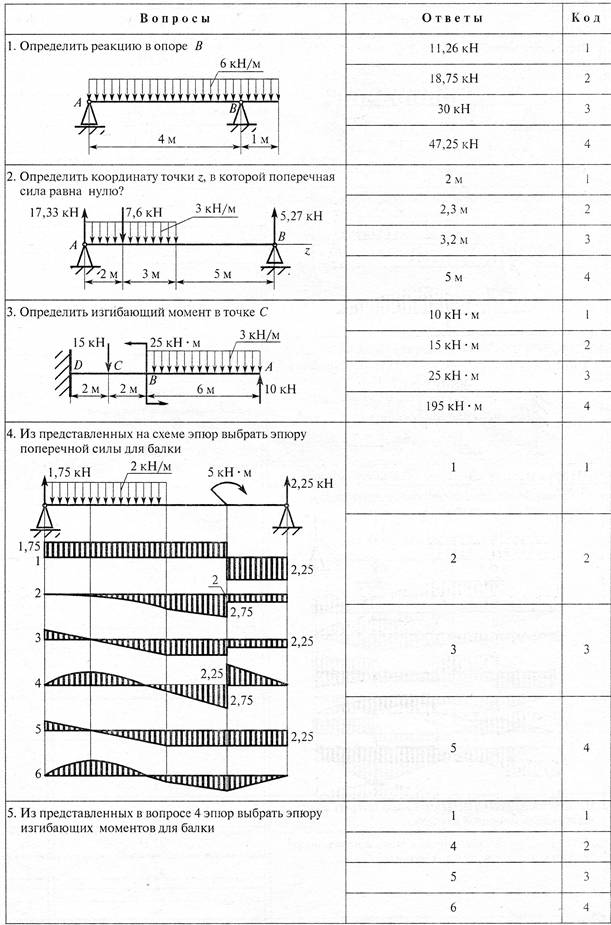 №62. Определить изгибающий момент в точке С: 15 кН∙м.  №63. Определить реакцию в опоре В: 8,4 кН.  №64. Определить поперечную силу в точке с координатой 2 м: -1,2 кН.  №65. Определить изгибающий момент в точке С: 67 кН∙м.  №66. Из представленных на схеме эпюр выбрать эпюру поперечной силы для балки: 1.  №67. Выбрать формулу для расчета изгибающего момента в сечении 3-3: 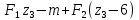 . .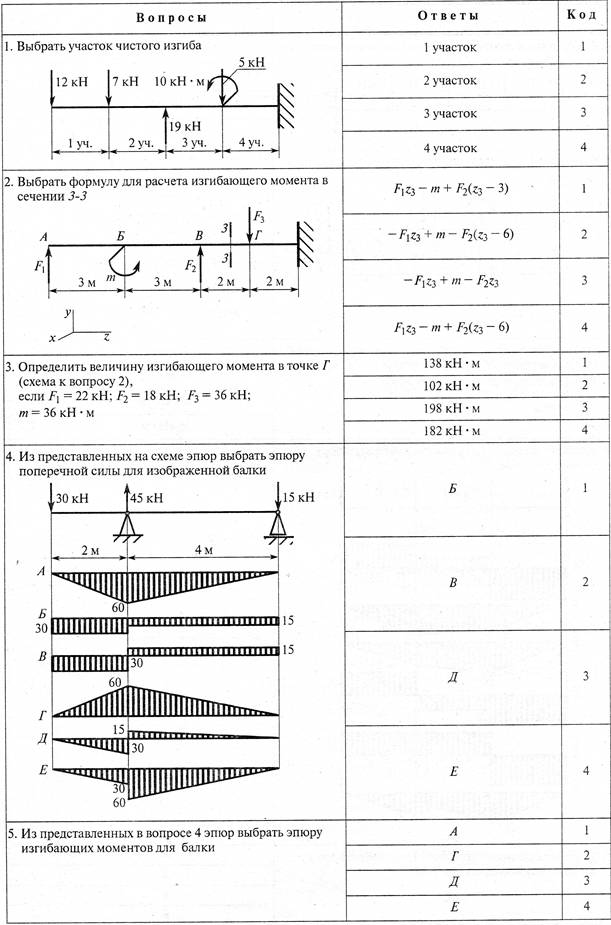 №68. Какому нагружению соответствует данная эпюра? 1. 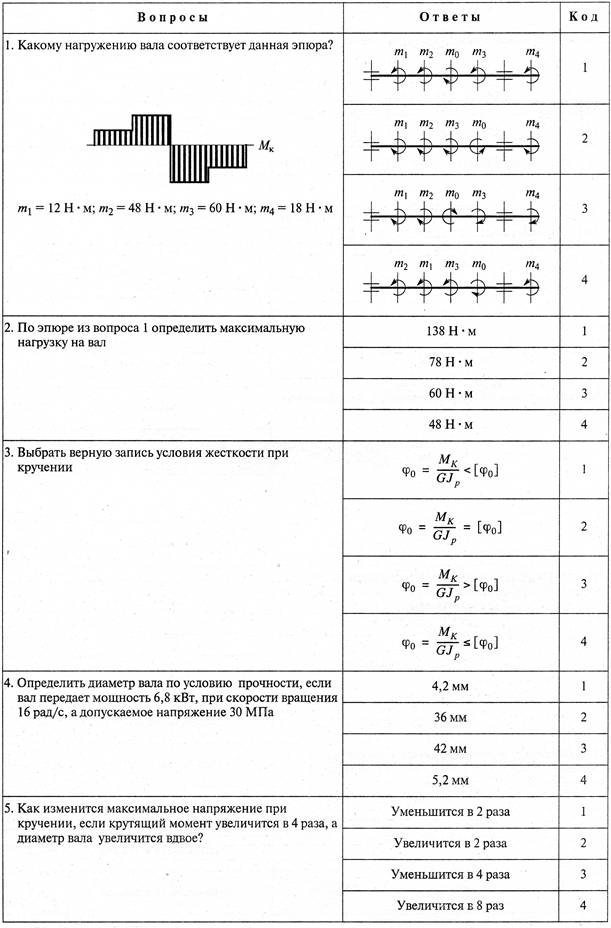  №69. Определить диаметр вала по условию прочности, если вал передает мощность 6,8 кВт, при скорости вращения 16 рад/с, а допускаемое напряжение 30 МПа: 42 мм. №70. Как изменится максимальное напряжение при кручении, если крутящий момент увеличится в 4 раза, а диаметр вала увеличится вдвое? Уменьшится в 2 раза. №71. От каких факторов зависит выделенная в формуле величина: от диаметра. №72. Проверить прочность бруса, если максимальный крутящий момент 80 Н∙м; диаметр бруса 25 мм; допускаемое напряжение 40 МПа: 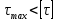 . .№73. От каких факторов зависит выделенная величина: от диаметра. №74. В каком случае значение 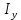 максимально? В. максимально? В.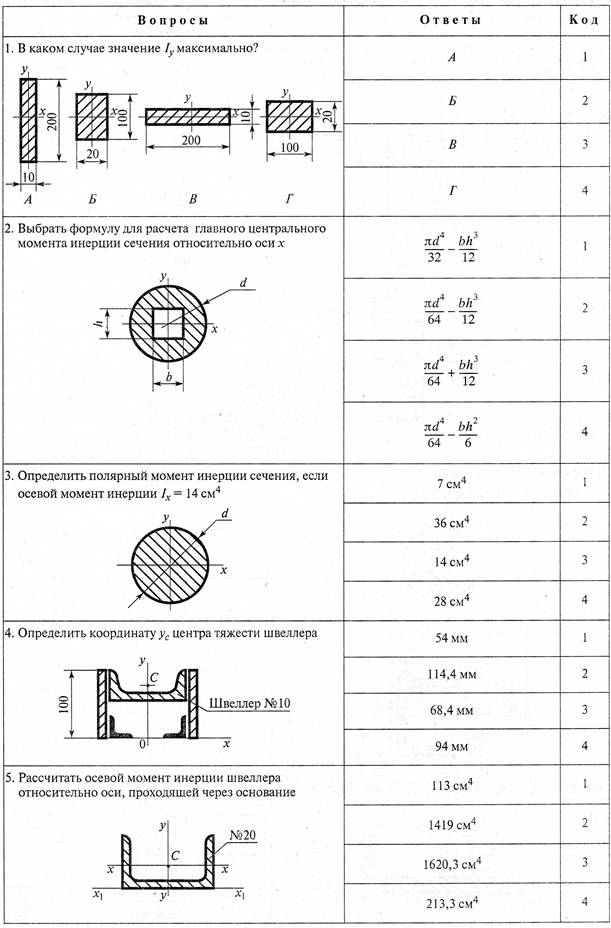 №75. Формулу Ясинского используют при расчетах: на устойчивость сжатых стержней за пределом пропорциональности. №76. Величина 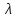 = =  , которая входит в формулу для критического напряжения в сжатом стержне , которая входит в формулу для критического напряжения в сжатом стержне  , называется: гибкостью стержня. , называется: гибкостью стержня.№77. Для стержней из малоуглеродистой стали формула Эйлера для критической силы применима, если гибкость стержня  : больше 100. : больше 100.№78. Критической силой сжатого стержня называется наименьшее значение сжимающей силы, при котором: стержень теряет способность сохранять прямолинейную форму равновесия. №79. Эпюра изгибающих моментов, построенная на сжатых волокнах, для балки имеет вид: Этой эпюре соответствует нагружение балки, представленное на рисунке:  №80. Консольная балка нагружена сосредоточенной силой Р. Осевой момент сопротивления поперечного сечения балки равен W.  Условие прочности для данной балки имеет вид: PL/W  . .№81. Эпюра крутящего момента имеет вид: 1.  №82. Вал имеет постоянное по длине сечение с полярным моментом сопротивления  . Условие прочности вала при допускаемом напряжении на кручение . Условие прочности вала при допускаемом напряжении на кручение  имеет вид: 3М/ имеет вид: 3М/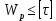 . . №83. Нормальное напряжение 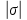 в точке К сечения 1-1 равно: 3FL/bh2. в точке К сечения 1-1 равно: 3FL/bh2. №84. Величина наибольшего значения изгибающего момента, возникающего в поперечном сечении балки, равна: FL/4.  №85. Единица измерения напряжения: Паскаль (Па). №86. Угол поворота  сечения балки от действия заданной нагрузки: 0. сечения балки от действия заданной нагрузки: 0. №87. При нагружении балки прямоугольного поперечного сечения высотой h и шириной b в сечении возникают изгибающий момент Мх и поперечная сила Qy.  Нормальные и касательные напряжения в точке А сечения соответсвенно равны:  ; ;  №88. В поперечном сечении балки при изгибе могут возникать внутренние силовые факторы: Q – поперечная сила и М – изгибающий момент. В сечении 1-1 балки, представленной на рисунке: есть М и Q.  №89. Угол  , на который каждое сечение поворачивается по отношению к своему первонаачльному положению, называется: углом поворота сечения балки. , на который каждое сечение поворачивается по отношению к своему первонаачльному положению, называется: углом поворота сечения балки.№90. Консольная балки нагружена сосредоточенным моментом М. Допускаемое напряжение для материала балки равно  . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W M/ M/ . . №91. Крутящий момент в сечении 1-1 по абсолютной величине равен: 2М.  №92. Приведенная на рисунке форма потери устойчивости сжатого стержня соответсвует способу закрепления стержня, показанному на схеме:  №93. Шарнирно опертая балка нагружена равномерно распределенной нагрузкой q. Допускаемое напряжение для материала балки равно  . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W . Условию прочности удовлетворяет осевой момент сопротивления поперечного сечения балки: W qL2/8 qL2/8 . . №94. Из условия прочности вала при допускаемом напряжении на кручение  полярный момент сопротивления Wp равен: Wp полярный момент сопротивления Wp равен: Wp 2М/ 2М/ . . №95. В резултате сжатия стального цилиндрического образца с площадью поперечного сечения 100 мм2 была получена диаграмма, представленная на рисунке. Предел текучести испытываемого материала равен: 800 МПа.  №96. При известных величинах P, d нормальное напряжение в точке О поперечного сечения стержня равно: - 4Р/  . .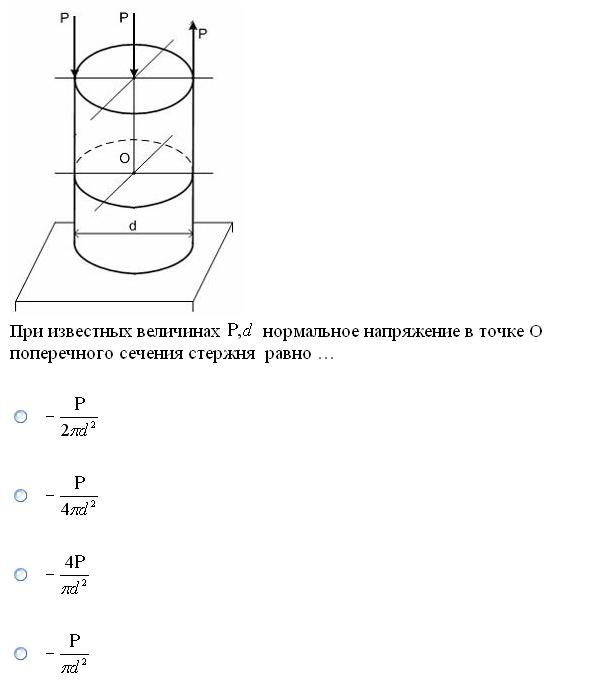 №97. Число канонических уравнений метода сил, которое необходимо составить для раскрытия статической неопределимости системы, показанной на рисунке, равно: трем. №98. Условие прочности штифта на срез имеет вид: 2F/  . .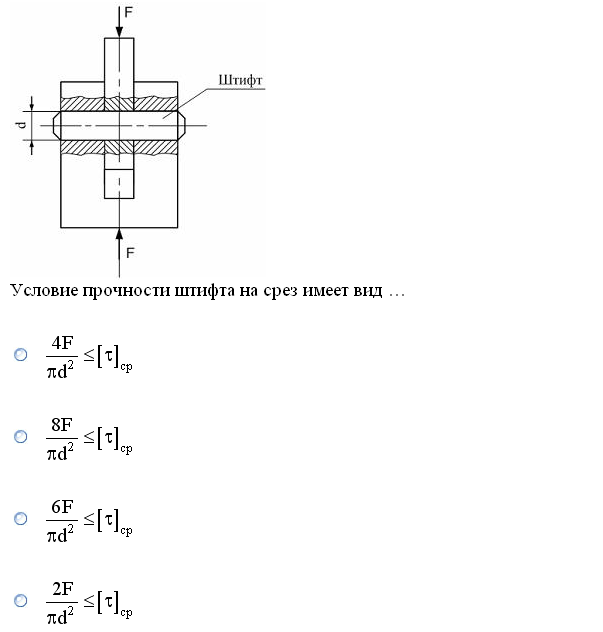 №99. Вид нагружения (сложного сопротивления) в сечении 1 стержня: изгиб с кручением. 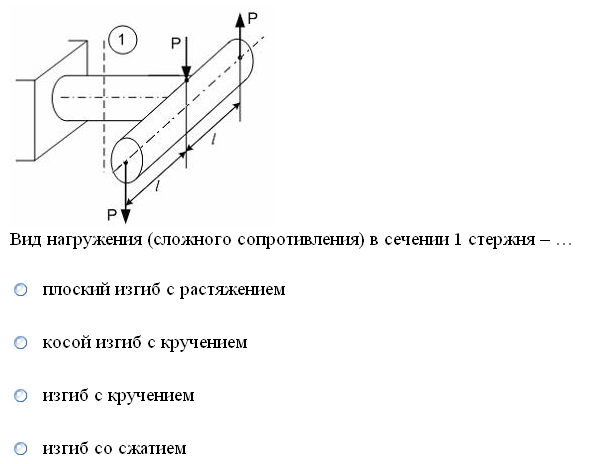 №100. Балка прямоугольного сечения нагружена усилиями P1 и Р2. В сечении С-С наиболее опасными будут точки: 2,3.  №101. Условие жесткости вала постоянного сечения при допускаемом относительном угле закручивания  (рад/м) имеет вид: 2М/GJp (рад/м) имеет вид: 2М/GJp . . №102. Сопротивление материалов – наука об инженерных методах расчета элементов машин и сооружений: на прочность, жесткость и устойчивость. |
