Техническая механика.. Пространственная система произвольно расположенных сил Произвольной пространственной системой сил
 Скачать 60.3 Kb. Скачать 60.3 Kb.
|
|
Пространственная система произвольно расположенных сил Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости. Отсюда вытекает условие равновесия произвольной пространственной системы сил. В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю R = 0, Mo = 0. В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю ΣFkx = 0, ΣFky = 0, ΣFkz = 0, Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0. Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений. Центр тяжести Центр тяжести тела - точка приложения силы тяжести (равнодействующей гравитационных сил). 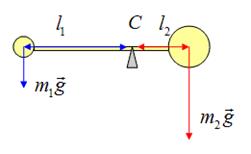  Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Определение центра тяжести Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы. Пусть тело состоит только из двух грузов с массами m1 и m2, соединенных стержнем (рис. 126). Если масса стержня мала по сравнению с массами m1 и m2, то ею можно пренебречь. На каждую из масс действует сила тяжести: P1=m1g, Р2=m2g; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы уже знаем, равнодействующая двух параллельных сил приложена в точке О, которая определяется из условия 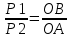 или или 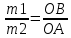 Следовательно, центр тяжести делит расстояние между двумя массами в отношении обратном отношению масс. Если это тело подвесить в точке О, оно останется в равновесии. Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: V = Ah, где А — площадь фигуры, h — ее высота. Тогда после подстановки в записанные выше формулы получим: где Ак — площадь части сечения; хк, ук — координаты ЦТ частей сечения. Выражение Координаты центра тяжести сечения можно выразить через статический момент: Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю. Смятие. Допускаемое напряжение. Условия прочности Довольно часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта в результате передачи нагрузки от одной поверхности к другой. При этом на поверхности возникают сжимающие напряжения, называемые напряжениями смятия, Расчет также носит условный характер. Однако при расчете боковой цилиндрической поверхности напряжения по поверхности распределены не равномерно, поэтому расчет проводят для наиболее нагруженной точки. Для этого вместо боковой поверхности цилиндра в расчете используют плоскую поверхность, проходящую через диаметр. Таким образом, условие прочности при смятии можно выразить соотношением 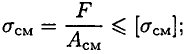 допускаемое напряжение смятия: Примеры деталей, работающих на сдвиг (срез) и смятие Ось (рис. 23.5). В случае, если толщина детали 2 меньше, 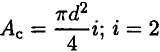 — количество площадей среза. — количество площадей среза.Болт. Шпонки работают на срез и смятие, но рассчитываются только на смятие. Заклепка односрезная, двухсрезная. 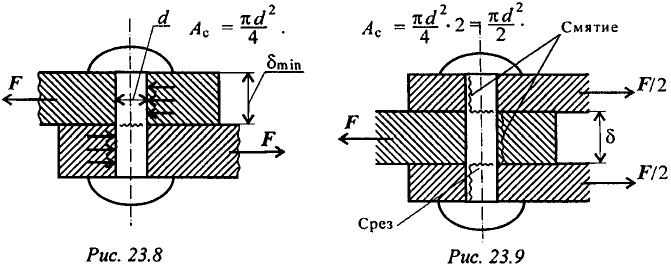 Сварное соединение (рис. 23.10). 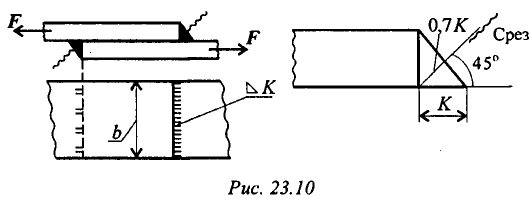 Угловой шов разрушается под углом 45° к плоскости разъема в результате среза. Двухсторонний шов: |
