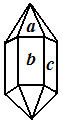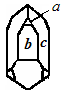|
|
курсовая. Шамурадов. Протокол от 2022 г
Кристаллы. Виды кристаллов.
Криста́ллы (от греч. κρύσταλλος, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл) — твёрдые тела, в которых атомы расположены закономерно, образуя трёхмерно-периодическую пространственную укладку — кристаллическую решётку.
Кристаллы — это твёрдые вещества, имеющие естественную внешнюю форму правильных симметричных многогранников, основанную на их внутренней структуре, то есть на одном из нескольких определённых регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).
Составляющие данное твёрдое вещество частицы образуют кристаллическую решётку. Если кристаллические решётки пространственно одинаковы или сходны (имеют одинаковую симметрию), то геометрическое различие между ними заключается, в частности, в разных расстояниях между частицами, занимающими узлы решётки. Сами расстояния между частицами называются параметрами решётки. Параметры решётки, а также углы геометрических многогранников определяются физическими методами структурного анализа. Часто твёрдые вещества образуют (в зависимости от условий) более чем одну форму кристаллической решётки; такие формы называются полиморфными модификациями.
Виды кристаллов
Следует разделить идеальный и реальный кристалл. Идеальный кристалл является, по сути, математическим объектом, имеющим полную, свойственную ему симметрию, идеализированно ровные гладкие грани ит.д. Реальный кристалл всегда содержит различные дефекты внутренней структуры решетки, искажения и неровности на гранях и имеет пониженную симметрию многогранника вследствие специфики условий роста, неоднородности питающей среды, повреждений и деформаций. Реальный кристалл не обязательно обладает кристаллографическими гранями и правильной формой, но у него сохраняется главное свойство — закономерное положение атомов в кристаллической решётке.
Большой одиночный кристалл, имеющий более или менее правильную форму, называют монокристаллом. Характерной особенностью монокристалла является анизотропия, то есть зависимость его физических свойств от направления в кристалле. Анизотропия механических свойств монокристалла сказывается, прежде всего в том, что его прочность в разных направлениях различна. При определенный условиях из расплавов металлов можно получить монокристаллы. Если же просто охладить расплавленное железо, то полученное твердое тело анизотропией обладать не будет. Причину этого помогает понять изучение структуры металла, под микроскопом можно увидеть, что оно состоит из отдельных зерен микроскопических размеров. Каждое такое зерно – это кристалл, который принял неправильную форму потому, что его росту помешали соседние кристаллики. Возникшая зернистая структура называется поликристаллической (поли - много). Поскольку все эти зерна ориентированы беспорядочно, то их анизотропия проявиться не может. Вследствие этого поликристалл изотропен, т. е. его свойства в среднем по всем направлениям одинаковы.
Строение кристаллов
Правильная многогранная форма кристалла, прежде всего, бросается в глаза наблюдателю, и она, конечно же, не составляет главную особенность кристаллического тела, но всё-таки я предлагаю обратить внимание на это явление - идеальную форму кристалла.
Форму, которую принимает монокристалл тогда, когда при его росте устранены все случайные факторы, называют идеальной. Идеальная форма кристалла имеет вид многогранника. Такой кристалл ограничен плоскими гранями, прямыми рёбрами и обладает симметрией. Как и всякий многогранник, кристалл имеет некоторое число граней P, рёбер R, вершин E, причём эти числа связаны между собой соотношением P+E=R+2. например, у куба 6 граней, 8 вершин и 12 рёбер (6+8=12+2). Для октаэдра, додекаэдра это соотношение также справедливо.
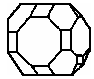 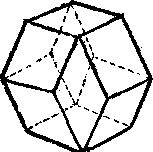 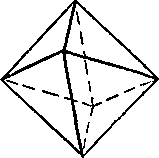
Рис 1. Рис 2 Рис 3.
Куб, октаэдр, додекаэдр представляют собой простые правильные многогранники. В форме правильных многогранников кристаллизуется сравнительно небольшое число кристаллов. В форме куба кристаллизуется поваренная соль, сернистый цинк, в форме октаэдров - алмаз, в форме ромбического додекаэдра - гранат. Чаще всего вещества кристаллизуются в виде сложных многогранников, т.е. они бывают ограничены несколькими сортами равных между собой граней. Так, например, кристалл имеет обычно 6 восьмиугольных граней, 8 шестиугольных граней и 12 четырёхугольных граней.
Кристаллы одного и того же вещества могут иметь весьма разнообразную форму. Форма кристалла зависит от условий кристаллизации. Цвет также не является характерным признаком кристаллов данного вещества, так как он очень сильно зависит от примесей. Известно, например, что кристаллы плавикового шпата могут быть бесцветными, розовыми, чёрными, фиолетовыми, тёмно-вишнёвыми и золотистыми. Казалось бы, что установление принадлежности двух кристаллов (отличающихся друг от друга и формой и цветом) одному веществу нельзя произвести иначе, как определив их химический состав. Однако кристаллографы установили на первый взгляд в высшей степени поразительный факт: в кристаллах одного вещества углы между соответственными гранями всегда одинаковы (закон постоянства углов).
Что понимают под соответственными гранями? В геометрии грани (плоские многоугольники) считаются равными, если они при наложении совпадают всеми своими точками. В кристаллографии равенство граней означает совершенно иное. Грани могут отличаться между собой по форме и всё-таки считаться равными, если они обладают одинаковыми физическими и химическими свойствами. Установить равенство граней в кристаллографическом смысле удаётся иногда путём внешнего их осмотра.
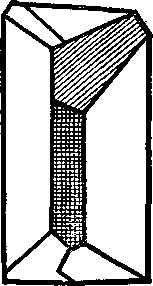 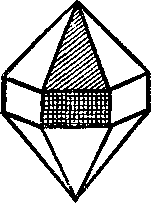 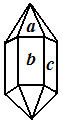 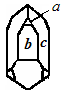
Рис 4. Рис 5.
На рисунке одинаковой штриховкой показаны одинаковые (равные) грани. В кристалле кварца можно установить три сорта граней. Хотя в разных кристаллах кварца грани a(b,c) имеют разный размер и форму, они считаются равными. Закон постоянства углов утверждает, что двугранный угол, образованный гранями a иb в различных кристаллах данного вещества, будет один и тот же. Соответственно во всех кристаллах данного вещества будут равны между собой и двугранные углы, образованные гранями a и c, b и c.
Итак, не форма кристаллов, не размер граней, а угол между ними является определенной величиной для каждого кристалла.
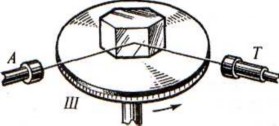 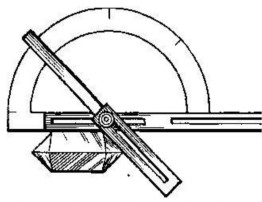
Рис. 6 Рис. 7
Для измерения углов между гранями применяют специальный прибор – гониометр. Прикладной гониометр (рис. 6) может быть применён для исследования крупных монокристаллов. Более точные измерения выполняют отражательным гониометром, схема которого дана на рисунке 7. Пучок света, идущий от источника А, попадает на грань кристалла и после отражения входит в зрительную трубку Т. При повороте кристалла на определённый угол пучок света вновь попадает в зрительную трубу. По шкале III гониометра отсчитывают угол между гранями. Измерив углы между гранями неизвестного кристалла, можно по специальному каталогу определить химический состав кристалла.
С явлением симметрии мы часто встречаемся в окружающей жизни. Симметрична бабочка (рис.8). Форма, рисунок и окраска левого крыла повторяет форму, рисунок и окраску правого.
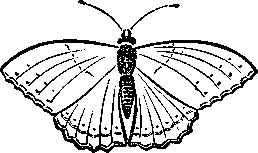 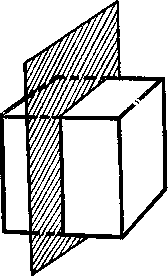
Рис.8 Рис.9
Если тело можно мысленно пересечь плоскостью так, что каждой точке a тела с одной стороны плоскости будет соответствовать точка b , лежащая по другую сторону плоскости и при том так, что прямая ab, соединяющая эти две точки, перпендикулярна плоскости и делится этой плоскостью пополам, то это тело обладает зеркальной симметрией. Сама плоскость называется в этом случае плоскостью симметрии. Например, плоскость, проведённая через середину рёбер куба параллельно его двум граням, служит плоскостью симметрии куба (рис.9). Куб имеет девять плоскостей симметрии.
Кроме зеркальной симметрии, тела могут обладать еще поворотной симметрией. Тело обладает поворотной симметрией, если при повороте на соответствующий угол все части фигуры совмещаются друг с другом. Ось, вокруг которой происходит вращение тела, называют осью симметрии. Смотря по тому, сколько раз совместится фигура сама с собой при одном полном повороте вокруг оси, ось симметрии имеет различный порядок (первый, второй, третий и т. д.).
Цветок ириса, например, обладает осью симметрии третьего порядка, снежинки – осью симметрии шестого порядка. В цветах очень часто наблюдается ось симметрии пятого порядка
Тела могут обладать ещё центром симметрии. Центр симметрии – точка в середине тела, относительно которой любая точка тела имеет другую соответствующую ей точку, лежащую на таком же расстоянии от центра в противоположном направлении. В телах может быть несколько плоскостей симметрии, несколько осей симметрии различного порядка, но не может быть больше одного центра симметрии.
Если в параллелограмме, отогнуть углы в противоположные стороны, то центр квадрата, получившегося в середине этой фигуры, будет центром симметрии, так как он делит пополам все прямые, попарно соединяющие одинаковые точки фигуры. Геометрический центр шара, куба, октаэдра является центром симметрии этих тел. Ось симметрии, плоскость симметрии и центр симметрии называют элементами симметрии.
Элементы симметрии обладают рядом свойств. Вот некоторые из них:
Пересечение двух плоскостей симметрии даёт ось симметрии.
Пересечение трёх взаимно перпендикулярных плоскостей симметрии даёт центр симметрии.
Идеальные формы кристаллов симметричны.
В кристаллах можно найти различные элементы симметрии: плоскость симметрии, ось симметрии, центр симметрии.
Рассмотрим симметрию некоторых простейших кристаллических форм. Кристаллы в форме куба (NaCl , KCl и др.) имеют девять плоскостей симметрии, три из которых проходят параллельно граням куба, а шесть – по диагоналям. Кроме того, куб имеет три оси симметрии 4-го порядка, четыре оси 3-го порядка и шесть осей 2-го порядка , кроме того, он имеет центр симметрии. Всего в кубе 1+9+3+4+6=23 элемента симметрии.
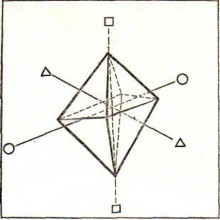 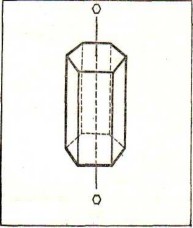 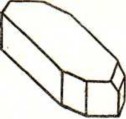
Рис. 10 Рис. 11 Рис. 12
Кристаллы алмаза, калиевых квасцов имеют форму октаэдров. Октаэдры обладают такими же элементами симметрии, что и кубы. показаны оси вращения октаэдра. У кристаллов медного купороса имеется лишь центр симметрии, других элементов симметрии у них нет.
Электрические свойства кристаллов
Электрические свойства кристаллов - свойства, связанные с электрической поляризацией, или самопроизвольной, или под влиянием внешних воздействий: нагревания, приложенного электрического поля, механического воздействия.
Электропроводимость
Электропроводность - свойство некоторых тел проводить электрических ток. Все вещества делятся на проводящие электрический ток (проводники), полупроводники и диэлектрики (изоляторы).
В проводниках, помещенных в электрическое поле, возникает электрический ток - направленное движение заряженных частиц. Хорошими проводниками являются металлы, с повышением температуры электропроводность металлов уменьшается. В отношении электропроводности кристалл выступает как непрерывная однородная среда.
Кристаллы-диэлектрики (ионные и ковалентные) при обычных условиях не проводят электрический ток. Их можно наэлектризовать путем различных воздействий: трением, давлением, облучением, нагреванием и т.п.
Проводники.
В некоторых веществах валентные электроны свободно перемещаются между атомами. Прежде всего, к этой категории относятся металлы, в которых электроны внешних оболочек буквально находятся в "общей собственности" атомов кристаллической решетки (Химические связи и Электронная теория проводимости). Если подать на такое вещество электрическое напряжение (например, подключить к двум его концам полюса аккумуляторной батареи), электроны начнут беспрепятственное упорядоченное движение в направлении южного полюса разности потенциалов, создавая, тем самым, электрический ток. Токопроводящие вещества подобного рода принято называть проводниками.
Самые распространенные в технике проводники - это, конечно же, металлы, прежде всего медь и алюминий, обладающие минимальным электрическим сопротивлением и достаточно широко распространенные в земной природе. Именно из них, в основном, изготавливаются и высоковольтные электрические кабели, и бытовая электропроводка. Имеются и другие виды материалов, обладающих хорошей электропроводностью, - это, в частности, солевые, щелочные и кислотные растворы, а также плазма и некоторые виды длинных органических молекул.
В этой связи важно помнить, что электропроводность может быть обусловлена наличием в веществе не только свободных электронов, но и свободных положительно и отрицательно заряженных ионов химических соединений. В частности, даже в обычной водопроводной воде растворено столько всевозможных солей, разлагающихся при растворении на отрицательно заряженные катионы и положительно заряженные анионы, что вода (даже пресная) является весьма хорошим проводником, и об этом нельзя забывать, работая с электрооборудованием в условиях повышенной влажности - иначе можно получить весьма ощутимый удар током.
Изоляторы
Во многих других веществах (в частности, в стекле, фарфоре, пластмассах) электроны прочно привязаны к атомам или молекулам и не способны к свободному перемещению под воздействием приложенного извне электрического напряжения. Такие материалы называются изоляторами.
Чаще всего в современной технике в качестве электроизоляторов используются различные пластмассы. По сути, любой пластик состоит из полимерных молекул - то есть очень длинных цепочек органических (водородно-углеродных) соединений, - которые, к тому же, образуют сложные и весьма прочные взаимные переплетения. Проще всего структуры полимера представить себе в виде тарелки перепутавшейся и слипшейся длинной и тонкой лапши. В таких материалах электроны прочно привязаны к своим сверхдлинным молекулам и не способны покинуть их под воздействием внешнего напряжения. Хорошими изоляционными свойствами обладают и аморфные вещества, такие как стекло, фарфор или резина, не имеющие жесткой кристаллической структуры. Они также нередко используются в качестве электроизоляторов.
В 1880 г. французские учёные-физики Пьер и Жак Кюри открыли пьезоэлектрический эффект.
Пьезоэлектрический эффект заключается в следующем.
Если из кристалла кварца (кварц-диэлектрик) вырезать определённым образом пластинку поместить её между двумя электродами, то при сжатии кварцевой пластинки на электродах появятся равные по величине, но различные по знаку заряды.
Если изменить направление силы, действующей на пластинку (вместо того чтоб сдавить кварц его будут растягивать), то изменяются и знаки зарядов на
электродах: на том электроде, где при сжатии возникал положительный заряд, при растяжении появится отрицательный. При этом, чем больше сила сжимающая или растягивающая пластинку, тем больше и величина зарядов, возникающая на электродах.
В середине XIX в. были также обнаружены диэлектрики, которые назвали электретами.
Самое характерное свойство электретов - способность нести на своих
противоположных сторонах заряды различного знака, которые могут сохраняться в течение весьма длительного времени. Так, для электретов из карнаубского воска и его смесей это время составляет годы, керамические электреты сохраняют заряд в течение двух лет, электреты из полимеров имеют время жизни месяцы.
Объяснить этот обширный экспериментальный материал об электрических свойствах диэлектриков стало возможным тогда, когда появилась теория, объясняющая строение твёрдых тел, связи между их структурными частицами.
Есть такие твёрдые тела, у которых центры положительных и отрицательных зарядов отдельных атомов или молекул совпадают.
Если такие вещества поместить в электрическое поле, то возникает "электрическая деформация" структурных частиц, т.е. электрическое поле смещает электрические заряды, входящие в состав диэлектрика, от тех положений, которые они занимали в отсутствие поля. Так, например, если диэлектрик состоит из нейтральных атомов, то в присутствии поля их электронные оболочки смещаются относительно положительно заряжённых ядер.
Если кристаллическая решётка твёрдого тела состоит из положительно и отрицательно заряжённых ионов, например, решетка NaCl, то в электрическом поле ионы равных знаков смещаются относительно друг друга. В результате упругого смещения каждой пары зарядов образуется система, обладающая некоторым дополнительным моментом p=ql, а весь диэлектрик поляризуется.
Помимо неполярных диэлектриков, существует большой класс диэлектриков, молекула которых и при отсутствии внешнего электрического поля обладают дипольным моментом. Постоянный дипольный момент могут иметь многие молекулы, у которых центры симметрии составляющих их положительных и отрицательных зарядов не совпадают друг с другом. Типичными представителями полярного твёрдого диэлектрика служат лед, твердая соляная кислота, органическое стекло и др.
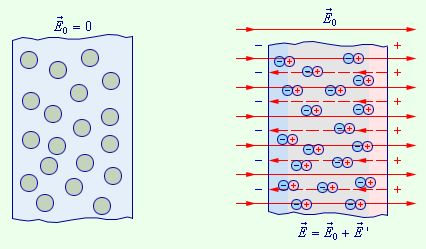
Рис. 13. Поляризация неполярного диэлектрика.
При помещении полярного диэлектрика в электрическое поле происходит ориентация полярных молекул так, чтобы их оси совпадали с направлением линий напряжённости электрического поля. Однако тепловое движение частиц вещества препятствует такой ориентации. В результате действия поля и теплового движения устанавливается равновесное состояние, при котором полярные молекулы приобретают в среднем некоторую направленную ориентацию, а весь диэлектрик благодаря этому приобретает дипольный момент в направлении поля, т.е. поляризуется.

Рис. 14. Ориентационный механизм поляризации полярного диэлектрика.
Рассмотренный вид поляризации называют ориентационной или дипольной. В этом виде поляризации, в отличие от поляризации смещения, существенную роль играет температура диэлектрика.
Диэлектрическая проницаемость полярных диэлектриков больше, чем у неполярных, так как у них по существу наблюдаются оба вида поляризации: ориентационная и упругая поляризация смещения.
Если внешнее поле убрать, то полярные и неполярные диэлектрики деполяризуются, т.е. поляризация их практически исчезает.
Существует третий тип диэлектриков, у которых наблюдается самопроизвольная поляризация. В этом случае внутри диэлектрика, без какого бы то ни было воздействия внешнего поля, самопроизвольно возникают однородно поляризованные области, так называемые домены. В отсутствии внешнего поля направления дипольных моментов областей различны. При наложении поля происходит "ориентация" доменов и весь диэлектрик поляризуется. Так как каждый домен имеет большой дипольный момент, то диэлектрическая проницаемость таких диэлектриков обычно очень велика, порядка 104.
Диэлектрики такого типа называют сегнетоэлектриками.
Сегнетоэлектрики отличаются от других диэлектриков рядом специфических свойств. Сегнетоэлектрики применяют при изготовлении лазеров и в запоминающих устройствах электронно-вычислительных машин.
И проводники, и изоляторы играют важную роль в нашей техногенной цивилизации, использующей электричество в качестве основного средства передачи энергии на расстоянии. По проводникам электроэнергия поступает от электростанций в наши дома и на всевозможные производственные предприятия, а изоляторы обеспечивают нашу безопасность, ограждая от губительных последствий прямого контакта человеческого организма с высоким электрическим напряжением.
Свет и его взаимодействие с кристаллом
Волновая модельсвета
Чтобы было проще понять поведение света, возьмем за основу простейшую волновую модель.
Плоские волны, независимо от их физической природы, характеризуются, по меньшей мере, двумя величинами: скоростью распространения ν и длиной волны λ. При этих условиях простейшей моделью волн будет плоская система черных и белых полос одинаковой ширины, движущихся с постоянной скоростью. Длинна волны λ в этом случае будет равна суммарной ширине одной черной и одной белой полосы. Если за единицу времени перед наблюдателем, смотрящим на эту картину в щель, пронесется η волн, то скорость должна быть равна: ν=ηλ.
Одновременно наблюдатель будет видеть, что в щели происходят колебания, т.е. она будет периодически, через равные промежутки времени Т/2, закрываться то белой, то черной полосой. Величина η называется частотой колебаний, величина Т – периодом колебаний. Эти величины обратны друг другу.
Видимая областьизлучения
Согласно данной теории, цвет мы будем рассматривать как монохроматические лучи с разными значениями длин волн. Приближенные значения длин волн лучей в пустоте выведены в таблице 1
Таблица 1.
ЦВЕТ
|
λ, мμ
|
ЦВЕТ
|
λ, мμ
|
ультрафиолетовый
|
<390
|
Зелено-желтый
|
550 – 575
|
фиолетовый
|
390 – 450
|
желтый
|
575 – 585
|
синий
|
450 – 480
|
оранжевый
|
585 – 620
|
голубой
|
480 – 510
|
красный
|
620 - 760
|
зеленый
|
510 - 550
|
инфракрасный
|
>760
|
Интерференционные явления, возникающие при прохождении света через кристаллические пластинки.
Наблюдение явлений интерференции света при прохождении поляризованного света через плоскопараллельные пластинки позволяет выяснить ряд свойств кристаллов, таких, например, как оптический класс кристаллов (т.е. является ли кристалл изотропным, одноосным или двуосным), позволяет отделить монокристаллические образцы от поликристаллических, определить оптический знак кристалла и ряд других свойств.
Начнем с рассмотрения явлений интерференции света при нормальном падении параллельного пучка поляризованного света на плоскопараллельную пластику, т.е. поместим кристаллическую пластинку между поляризатором и анализатором и осветим систему параллельным пучком света с длиной волны λ . Тогда в кристалле будут распространяться две волны, поляризованные в 2-х взаимно-перпендикулярных плоскостях. Эти волны будут распространяться с разной скоростью. Поэтому на выходе пластинки будут складываться два взаимно-перпендикулярных колебания, имеющие разность фаз δ, приобретенную за счет различной скорости распространения в кристалле с толщиной d
δ = 2λπ d (n1 − n2 ), (3)
где n1 и n2 - два значения показателя преломления света для двух волн различной поляризации. В результате на выходе пластинки свет будет уже не линейно поляризованным, а эллиптически поляризованным. В частном случае этот эллипс может вырождаться в пря мую. Так, если разность фаз кратна 2π, то свет будет поляризован так же как и до входа в пластинку.
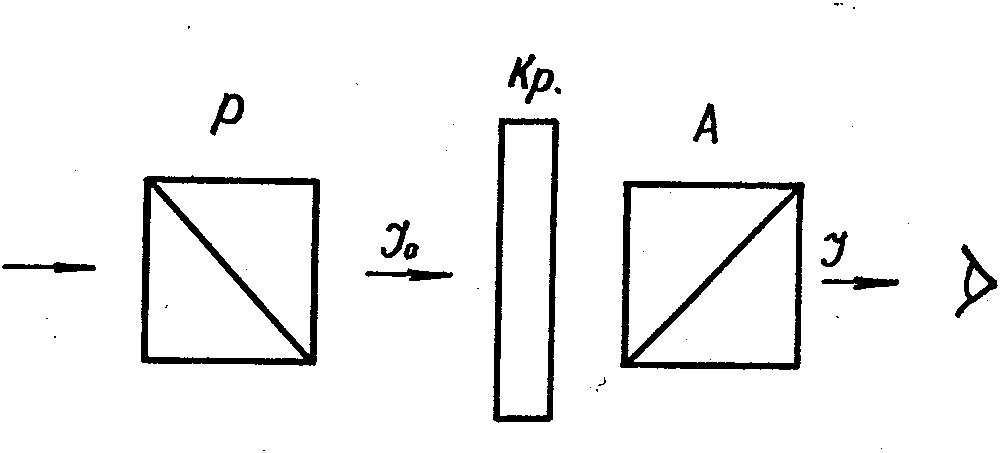 Рис. 15. Оптическая схема для наблюдения интерференции света, прошедшего через кристаллическую пластинку. Р – поляризатор, А – анализатор, Кр –кристаллическая плоско-параллельная пластинка. Рис. 15. Оптическая схема для наблюдения интерференции света, прошедшего через кристаллическую пластинку. Р – поляризатор, А – анализатор, Кр –кристаллическая плоско-параллельная пластинка.

2
Интенсивность света, прошедшего через анализатор, будет зависеть от взаимной ориентации анализатора и поляризатора. В том случае, когда анализатор и поляризатор скрещены, интенсивность прошедшего света определяется выражением 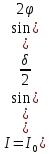 (4) (4)
где I0 - интенсивность света, падающего на кристалл, а φ - угол между направлением колебаний, пропускаемых поляризатором, и направлением вектора индукции
D одной из двух волн, могущих распространяться в кристалле (здесь не учитываются потери на отражение).
Если на кристалл падает не монохроматический свет, а белый, и если принять, что амплитуды колебаний в падающем свете для всех длин волн одинаковы, то при прохождении такого света через систему, изображенную на рис. 15, спектральный состав света будет изменен, поскольку величина δ зависит от длины волны. Из формулы (4) сразу видно, что если оставить неподвижными анализатор и поляризатор, то при вращении кристалла во круг оптической оси интенсивность прошедшего света четыре раза обратится в нуль при повороте пластинки на 360° одновременно для света всех длин волн. Интенсивность света обращается в нуль, когда направление колебаний векторов индукции волн, могущих рас пространяться в кристалле, совпадает с направлением колебаний, пропускаемых поляриза тором.
Второй важный вывод, вытекающий из рассмотрения прохождения белого света через оптическую систему, изображенную на рис. 15, состоит в том, что распределение интенсивности в спектре прошедшего света как уже было сказано будет иным по сравнению с падающим. Свет тех длин волн, для которых состояние поляризации на выходе пластинки остается таким же, каким оно было на входе, не пройдет через анализатор. Свет этих волн будет отсутствовать в прошедшем свете. Свет близлежащий длин волн будет сильно ослаб лен. Если толщина кристалла невелика, т.е., если разность хода 2-х волн, распространяющихся в кристалле не превышает нескольких длин волн, то прошедший свет по спектральному составу будет сильно отличаться от падающего. График зависимости интенсивности прошедшего через систему света от длины волны, когда d (n1 − n2 ) = 600 нм.
Если толщина пластинки такова, что в пределах видимого света от 400-700 нм укладывается один максимум интенсивности прошедшего света, пластинка кажется окрашенной в тот цвет, которому соответствует максимальное значение интенсивности прошедшего света. Подобное рассмотрение позволяет понять принцип действия двух компенсаторов, при меняемых в дальнейшем в этой задаче.
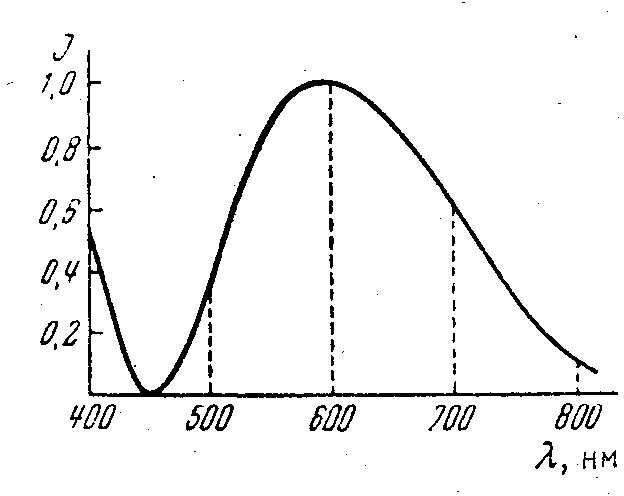
Рис. 16. График зависимости интенсивности (в условных единицах) света, прошедшего через систему, изображенную на рис. 15, при скрещенных поляризаторах от длины волны света
Первый компенсатор – это так называемая пластинка «чувствительного оттенка». Она представляет собой кварцевую плоскопараллельную пластинку, вырезанную параллельно оптической оси (направление оптической оси указано на оправе пластинки и обозначено там как Ng). Толщина пластинки такова, что вносимая ею разность хода d (ne − no ) = 555 нм.
Тогда, согласно сказанному выше, свет с длиной волны 555 нм на выходе будет иметь ту же поляризацию, что и на входе пластинки, т.е. анализатор не пропускает свет с указан ной длиной волны.
Таким образом, из белого света будет изъята зеленая часть спектра. Пластинка будет казаться окрашенной в фиолетово-красный цвет при наблюдении в скрещенных николях. Если теперь на пути лучей ввести дополнительную разность хода, то уже при небольшом увеличении разности хода пластинка кажется окрашенной в синий цвет (минимум пропускания сместится в красную сторону). Если разность хода несколько уменьшить, то окраска становится оранжевокрасной. Пластинка «чувствительного оттенка» применяется для обнаружения небольших разностей хода лучей.
Второй компенсатор – это кварцевый клин. Обычно он вырезан так, что угол его имеет величину около 0.5° и длина клина составляет 5 см, так что максимальная толщина клина 0,5 мм. Оптическая ось кварца обычно бывает параллельна ребру клина и ее направление указано на оправе клина (обозначение Ng) Если такой клин поместить между скрещенны ми николями так, чтобы оптическая ось клина составила угол 45° с направлением колебаний, пропускаемых поляризатором и направить на систему белый свет, то различные по толщине места клина будут окрашены в разные цвета. Наблюдаемое чередование цветов при скрещенных поляризаторах приведено в следующей таблице, где первая колонка со держит значения разности хода, вторая соответствующую ей окраску.
Таблица.
Разность хода d (ne –no)
(нм)
|
Цвет в скрещенных поляризаторах
|
№ порядка
|
260
|
белый
|
1
|
300
|
желтый
|
500
|
оранжевый
|
550
|
красный
|
565
|
малиновый
|
2
|
590
|
синий
|
660
|
голубой
|
728
|
зелено-голубой
|
840
|
зелено-желтый
|
910
|
желтый
|
950
|
оранжевый
|
1100
|
светло-малиновый
|
1130
|
серо-голубой
|
3
|
1380
|
зеленый
|
1430
|
желтый
|
1530
|
оранжевый
|
1650
|
беловато-малиновый
|
1710
|
зеленый
|
4
|
2000
|
серый
|
2050
|
светло-красный
|
При разности хода, равной 555 нм, наблюдается, как мы уже говорили, фиолетово-красный оттенок, который повторяется при увеличении разности хода в два, три и т.д. раза. Поэтому все интерференционные полосы условно делятся на полосы 1, 2, 3,… порядков в зависимости от разности хода, вносимой пластинкой. При разности хода, лежащей в интервале от 0 до 555 нм, говорят о полосах первого порядка, при разности хода от 555 нм до 1100 нм говорят о полосах второго порядка и т.д. Определяемый таким образом порядок интерференции указан в третьем столбце таблицы. Пластинка «чувствительного оттенка» и кварцевый клин применяются в дальнейшем для определения оптического знака кристалла.
Отражениесвета
Если свет падает на плоскую и гладкую поверхность раздела двух прозрачных изотропных сред, то он отражается, следуя законам: 1) падающий и отраженный лучи лежат в одной плоскости нормалью к отражающей поверхности, 2) угол падения равен углу отражения
Преломлениесвета
Когда пучок света переходит из менее плотной изотропной среды в более плотную перпендикулярно границе между ними, то его скорость уменьшается, но не меняется направление движения.
Однако, когда пучок света падает на границу раздела сред под острым углом, снижение скорости на этой границе заставляет лучи изгибаться, или преломляться. Преломление происходит по следующим законам: 1) луч падающий и луч преломленный лежат в одной плоскости с нормалью к преломляющей поверхности, 2) отношение синуса угла падению к синусу угла преломления есть величина постоянная для данной пары сред, не зависящая от угла падения. Эта величина, обозначаемая n, называется показателем преломления среды, в которую вошел луч, относительно среды, из которой он вышел. Если, говоря о показателе преломления какой-либо среды, не указывают другую, то имеют в виду показатель преломления данной среды относительно пустоты, т.е. предполагают, что свет идет из пустоты в данную среду.
Показатель преломления вещества, так же как и плотность, зависит от его химического состава и кристаллической структуры. Удельный вес (G) и показатель преломления приближенно связаны соотношением: (n-1)/G = K, где K – константа, зависящая от состава вещества.
Явление преломления света было известно еще до нашей эры, но точные законы преломления были установлены Снеллиусом, профессором математики в Лейдене (Голландия), только в 1618г и независимо от него Декартом в 1637г.
Когда луч света идет из более преломляющей среды в менее преломляющую, то, по закону преломления, показатель преломления больше 1. Будем постепенно увеличивать угол падения, пока он не примет максимального значения, допускаемого формулой. При таком значении угол отражения становится равным 90 градусов, а его синус равным единице. Следовательно, если угол падения будет больше максимально допустимого значения, то синус его должен быть больше единицы, что невозможно. Значит, при угле падения, который больше максимального, преломление отсутствует. В этом случае свет полностью отражается. Такое отражение называется полным внутренним.
Дисперсиясвета
Существует еще одно явление, известное с древности, но изученное не очень давно. Ньютон в 1672г экспериментально показал, что луч белого света, проходя через стеклянную призму, разлагается в спектр, состоящий из множества лучей разного света, от красного до фиолетового, постепенно переходящих один в другой. Явление разложения белого света, называемое дисперсией, указывает на то, что лучи разной окраски имеют различный показатель преломления. При нормальной дисперсии, наблюдаемой в неокрашенных прозрачных средах, красный свет имеет наименьший, а фиолетовый наибольший показатель преломления. При аномальной дисперсии, наблюдаемой в окрашенных средах, этот порядок нарушается в том месте спектра, где происходит поглощение света. Свет какой-либо одной спектральной окраски называется монохроматическим. Строго монохроматический свет получит невозможно, так как для этого пришлось бы выделить из спектра бесконечно узкую линию. Яркость такого цвета была бы бесконечно мала. И видеть такой свет мы не могли бы.
Эти два явления вполне могут дать ответ на вопрос о том, почему граненые драгоценные камни играют всеми цветами радуги. Форма, которую придают камню при огранке, не случайна. Она подбирается так, чтобы каждый луч, вошедший в граненый камень, не прошел сквозь камень, а после преломления и отражения в других гранях, повернул бы обратно. Для этого существуют свои законы, приемы и расчеты. Иногда при огранке, стачивая ненужные углы, приходится жертвовать почти половиной камня. Известны случаи, когда после огранки оказывалось, что форма подобрана неудачно, и приходилось перегранивать камень. так пришлось перегранить один из самых больших в мире алмазов «Коинур». По преданию, алмаз в необработанном виде весил 180 граммов. После первой огранки он весил лишь 37 граммов, а после второй – потерял в весе еще 16 граммов.
Своеобразные явления, связанные с отражением и преломлением света, можно наблюдать и на естественно ограненных кристаллах. Примером могут служить фотографии, снятые академиком А.В.Шубниковым таким образом, что пучок света был пропущен сквозь многогранный кристалл, а за кристаллом стояла фотографическая пластинка. Проходя через кристалл, свет преломлялся на разных гранях. Поэтому на фотографической пластинке остался след не одного луча, а многих; узоры получились очень правильными и симметричными, потому что грани в кристалле расположены симметрично.
|
|
|
 Скачать 206.11 Kb.
Скачать 206.11 Kb. Рис. 15. Оптическая схема для наблюдения интерференции света, прошедшего через кристаллическую пластинку. Р – поляризатор, А – анализатор, Кр –кристаллическая плоско-параллельная пластинка.
Рис. 15. Оптическая схема для наблюдения интерференции света, прошедшего через кристаллическую пластинку. Р – поляризатор, А – анализатор, Кр –кристаллическая плоско-параллельная пластинка.
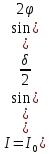 (4)
(4)