практические нгпо. Гидрогазодинамика. Протокол 09 от 08 сентября 201 8 г. Автор Кузьминский Р. А., к в. н., профессор
 Скачать 3.23 Mb. Скачать 3.23 Mb.
|
Методические указания к решению задачи № 22.1. По мере движения газа по соплу (рис.1.4), его абсолютная температура Т и давление р снижаются, а скорость w возрастает (рис. 2.2). 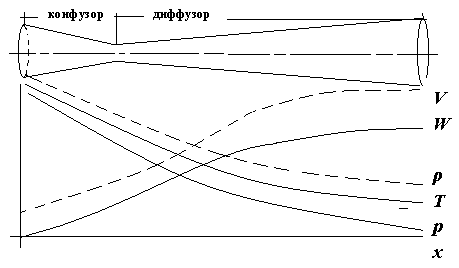 Рис. 2.2. Скорость газа в узком сечении определяется по уравнению 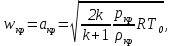 а на выходе из сопла по уравнению 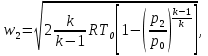 в котором р2=рн. Максимальная скорость на выходе из сопла Лаваля достигается при истечении в абсолютный вакуум, когда рн/р2=0. Массовый расход газа G через сопло Лаваля определяется по уравнению 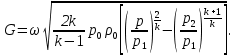 При этом принимаются параметры либо в критическом (узком) сечении, либо в выходном сечении сопла. При определнии G по параметрам узкого сечения принимаются ω=ωкр, р=ркр=p0βкр, а параметрам выходного сечения ω=ω2, р=р2=рн (здесь рн – давление на срезе сопла). Максимальный расход газа ограничивается узким сечением сопла, когда скорость в нем равна скорости звука и β=βкр, (р/р0=ркр/р0). Так как при β<βкр в узком сечении р/р0=ркр/р0=const, то и массовый расход газа остается неизменным, равным максимальному. Решение задачи рекомендуется выполнять в следующей последовательности: 1. Расчёт параметров газа в критическом сечении. Находим газовую постоянную для кислорода: 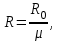 Дж/(кг·К), Дж/(кг·К),где R0 - универсальная газовая постоянная; – молярная масса кислорода. Из уравнения Менделеева - Клапейрона находим плотность газа при полной остановке: 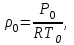 кг/м3. кг/м3.Находим скорость звука при полной остановке газа: 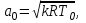 м/с, м/с,где k – показатель адиабаты, равный 1,41 для двухатомного газа. Определим скорость звука в критическом сечении: 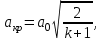 м/с. м/с.Максимальную скорость газового потока находим по формуле: 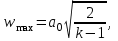 м/с. м/с.При расчёте будем пользоваться следующими газодинамическими функциями: 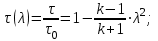 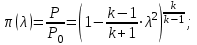 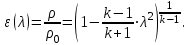 В критическом сечении коэффициент скорости wкр и число Маха Мкр равны единице: 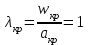 , откуда находим скорость газового потока в критическом сечении: , откуда находим скорость газового потока в критическом сечении: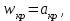 м/с; Мкр=1. м/с; Мкр=1.Используя газодинамическую функцию (λ), находим температуру газа в критическом сечении: 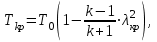 К; К;Рассчитаем давление газа в критическом сечении, используя газодинамическую функцию (λ): 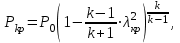 Па; Па;Найдём плотность газа в критическом сечении, используя газодинамическую функцию (λ): 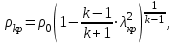 кг/м3; кг/м3;Из уравнения неразрывности потока находим площадь критического сечения: 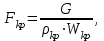 м2; м2;Находим диаметр критического сечения: 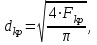 м; м;2. Расчёт параметров газа во входном сечении. Находим коэффициент скорости во входном сечении: 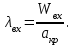 ; ;Используя газодинамическую функцию (λ), находим температуру газа во входном сечении: 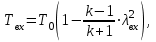 К; К;Рассчитаем давление газа во входном сечении, используя газодинамическую функцию (λ): 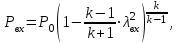 Па; Па;Найдём плотность газа во входном сечении, используя газодинамическую функцию (λ): 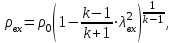 кг/м3; кг/м3;Из уравнения неразрывности потока находим площадь входного сечения: 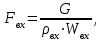 м2; м2;Находим диаметр входного сечения: 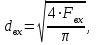 м; м;Вычисляем скорость звука во входном сечении: 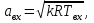 м/с; м/с;Определяем число Маха во входном сечении: 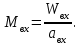 ; ;3. Расчёт параметров газа в выходном сечении. Давление газа в выходном сечении Рвых равно давлению на срезе сопла Рср, т. е. р2, Рвых=Рср= р2, МПа. Используя газодинамическую функцию (λ), находим коэффициент скорости в выходном сечении: 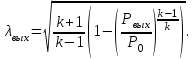 ; ;Используя газодинамическую функцию (λ), находим температуру газа в выходном сечении: 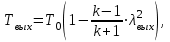 К; К;Найдём плотность газа в выходном сечении, используя газодинамическую функцию (λ): 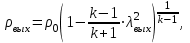 кг/м3; кг/м3;Определим скорость газового потока в выходном сечении: 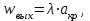 м/с; м/с;Из уравнения неразрывности потока находим площадь выходного сечения: 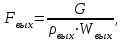 м2; м2;Находим диаметр выходного сечения: 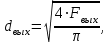 м; м;Вычисляем скорость звука в выходном сечении: 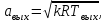 м/с; м/с;Определяем число Маха в выходном сечении: 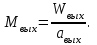 ; ;4. Геометрический профиль сопла. Определяем длину суживающейся (дозвуковой) части сопла: 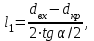 м; м;Находим длину расширяющейся (сверхзвуковой) части сопла: 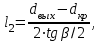 м; м;Вычисляем общую длину сопла: 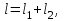 м; м;Геометрический профиль сопла показан на рис. 1.3. 5. Расчёт дополнительных сечений. Для расчета принимаются два дополнительных сечения в промежутке между входным и критическим сечениями и два дополнительных сечения в промежутке между критическим и выходным сечениями. Используя значения скорости во входном, критическом и выходном сечениях, устанавливаем скорость газа в принятом дополнительном сечении, например, в сечении 1 - w1. Далее расчет ведем в следующей последовательности: Находим коэффициент скорости в выбранном сечении 1 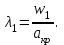 Используя газодинамическую функцию (λ), находим температуру газа в сечении 1: 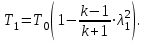 К КРассчитаем давление газа в сечении 1, используя газодинамическую функцию (λ): 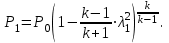 Па ПаНайдём плотность газа в сечении 1, используя газодинамическую функцию (λ): 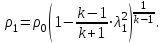 кг/м3 кг/м3Из уравнения неразрывности потока находим площадь сечения 1: 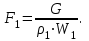 м2 м2Находим диаметр сечения 1: 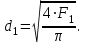 м мРасстояние между сечением 1 и критическим сечением: 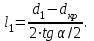 м мВычисляем скорость звука в сечении 1: 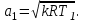 м/с; м/с;Определяем число Маха в сечении 1: 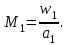 Аналогично рассчитываем параметры в сечениях 2, 3 и 4. Данные расчета параметров для основных (входного, критического и выходного) и дополнительных сечений 1, 2, 3, 4 заносим в таблицу 2.1.
С помощью данных таблицы параметров в основных (входного, критического и выходного) и дополнительных сечениях 1, 2, 3, 4 строим графики зависимости Р, T, w, a, ρ по длине сопла (см. рис. 2.3). 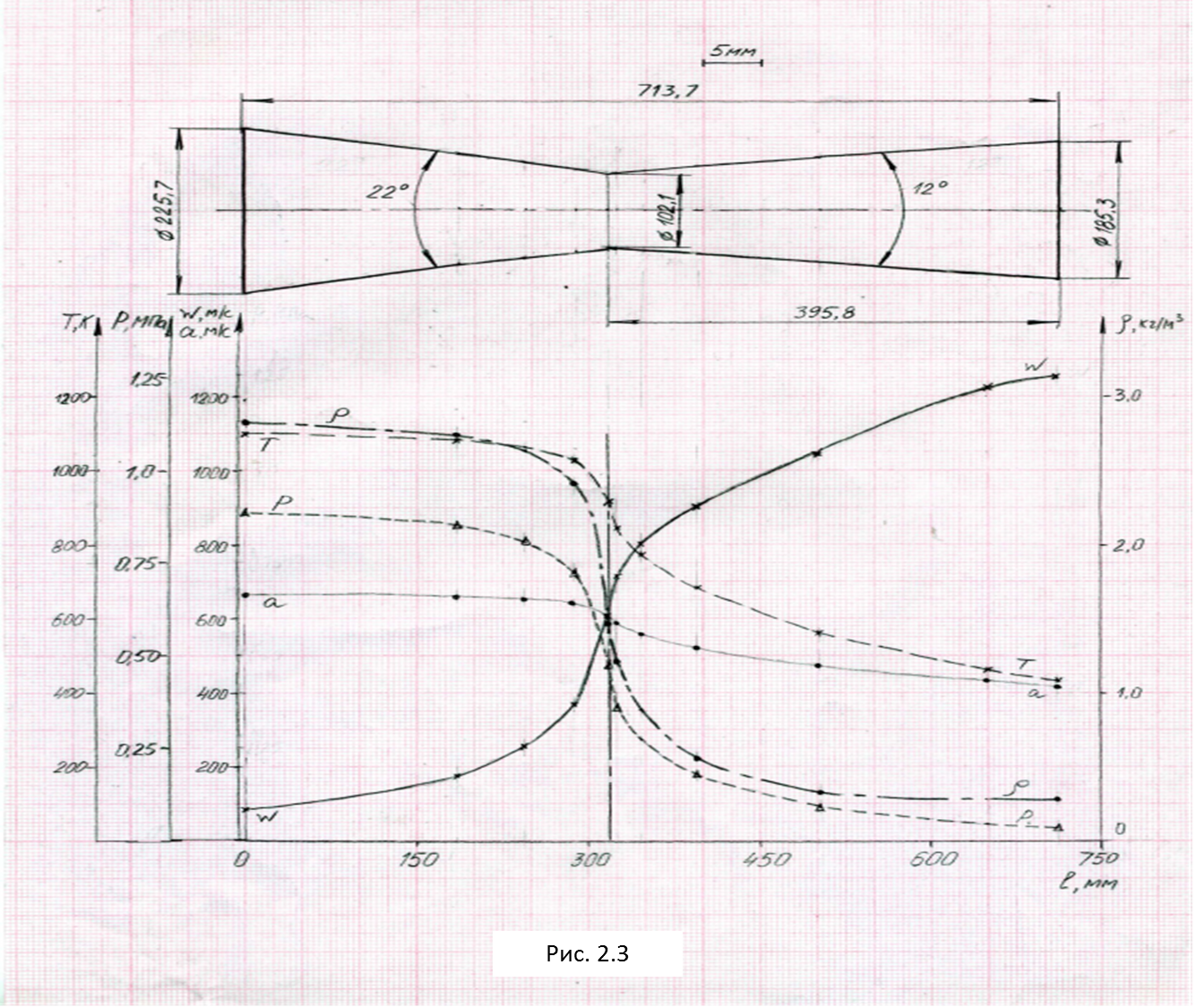 2.2. Прямой скачок уплотнения возникает только в сверхзвуковом потоке (λ1>1), при этом за скачком поток всегда становится дозвуковым (λ2<1). Изменение параметров газа при переходе через скачок имеет вид: Нужно знать, что всегда скорости газа до и после скачка связаны соотношением λ1λ2=1. Изменения параметров газа при переходе через скачок имеют вид: 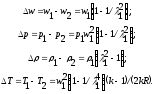 где λ1 = w1/aкр. Критическая скорость звука может быть определена из отношения 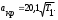 Используя приведенные зависимости, определяют скорость течения газа w2. Параметры заторможенного потока находим, используя зависимости: 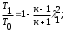 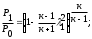 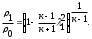 Литература Основная литература: 1. Штеренлихт А.Б. Гидравлика. Учебник. - М.: Колосс, 2009. 2. Кузьминский Р.А. Гидрогазодинамика. Учебное пособие. – М.: МИИТ, 2011. 3. Давидсон В.Е. Основы гидрогазодинамики в примерах и задачах. Учебное пособие. - М.: Издательский центр «Академия», 2008. Дополнительная литература: 1. Бекнев В.С. и др. Сборник задач и упражнений по газовой динамике. - М.: Машиностроение, 1992. 2. Альтшуль А. Д. Гидравлика и аэродинамика. - М.: Стройиздат, 1987. 3. Бондарев Е.Н. и др. Аэрогидродинамика. - М.: Машиностроение, 1993. 4. Давидсон В.Е. Основы газовой динамики в задачах. - М.: Высшая школа, 1987. 5. Самойлович Г.С. Гидрогазодинамика. - М.: Машиностроение, 1990. 6. Большаков В.А., Константинов Ю. М. и др. Справочник по гидравлике. - Киев: Вища школа, 1977. 7. Шевелев Ф.А., Шевелев А.Ф. Таблицы для гидравлического расчета водопроводных труб. Справочное пособие. - М.: Стройиздат,1987. 8. Журнал. Водоснабжение и санитарная техника. Приложение 1 Предельные расходы Q, л/с и скорости v, м/с в водопроводных трубах
Приложение 2 Удельные сопротивления S0, с2/м6 и расходные характеристики К, м3/с для бывших в эксплуатации водопроводных труб при скорости v 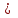 1,2 м/с 1,2 м/с
Приложение 3 Значение коэффициента К1 в зависимости от средней скорости v
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
