КСП по географии 7 класс. Типовой расчет Функции нескольк переменных (без ответов). Протокол 5 от 22. 12 2007г Зав кафедрой вм о. Е. Дейвальт Количество заданий 23 варианта Рудный 2007 1
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
2. Доказать, что 3. Найти полный дифференциал функции 4. Написать уравнение касательной плоскости к поверхности 5. Для функции 6. Вычислить приближенно с помощью полного дифференциала 7. Найти наибольшее и наименьшее значения функции 8. Найти производную функции 9. Методом наименьших квадратов найти формулу у =
10. Доказать, что выражение 22 ВАРИАНТ 1. Найти и изобразить область существования функции 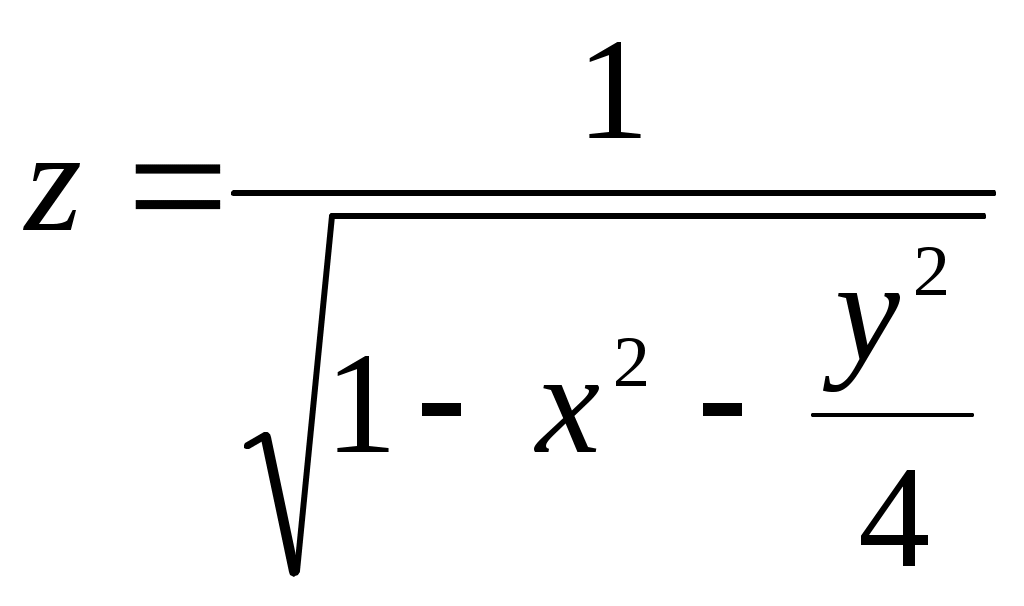 . Построить линии уровня данной функции . Построить линии уровня данной функции2. Доказать, что 3. Найти полный дифференциал функции Определить плоскость, касательную к поверхности Вычислить приближенно с помощью полного дифференциала 1,05 2,02 + 2,02 1,05 6. Для функции 7. Найти наибольшее и наименьшее значения функции Найти производную функции и = хуz в направлении, составляющем с осями координат равные углы в точке (1; 2; 1). 9. Методом наименьших квадратов найти формулу
10. Доказать, что выражение 23 ВАРИАНТ 1. Найти и изобразить область существования функции 2. Доказать, что 3. Вычислить приближенно с помощью полного дифференциала 4. Написать уравнение касательной плоскости к поверхности 5. Найти наибольшее и наименьшее значения функции 6. Найти полный дифференциал функции 7. Для функции 8. Найти производную функции 9. Методом наименьших квадратов найти формулу
10.Доказать, что выражение (соs (x + y2) + sinx) dx + 2ycos(x + y2) dy есть полный дифференциал некоторой функции z и найти ее. |
