Практ 3. Проверка статистических гипотез
 Скачать 112.61 Kb. Скачать 112.61 Kb.
|
|
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Пример. Для проверки эффективности новой технологий отобраны две группы рабочих : в первой группе численностью n1=50чел., где применялась новая технология ,выборочная средняя выработка составила 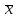 =85(изделий),во второй группе численностью n2=70чел.,выборочная средняя - =85(изделий),во второй группе численностью n2=70чел.,выборочная средняя -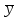 =78(изделий). Предварительно установлено, что дисперсии выработки в группах равны соответственно =78(изделий). Предварительно установлено, что дисперсии выработки в группах равны соответственно 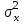 =100 и =100 и 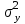 =74. На уровне значимости α =0,05выяснить влияние технологии на среднюю производительность. =74. На уровне значимости α =0,05выяснить влияние технологии на среднюю производительность.Решение: Проверяемая гипотеза Но: 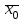 = = 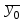 .т.е.средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взять Н1: .т.е.средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взять Н1: 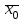 > >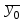 или Н2: или Н2: 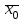 ≠ ≠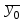 .(в данной задаче более естественна гипотеза Н1,так как ее справедливость означает эффективность применения новой технологии). .(в данной задаче более естественна гипотеза Н1,так как ее справедливость означает эффективность применения новой технологии).Фактическое значение статистики критерия 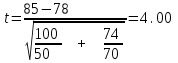 При конкурирующей гипотезе Н1 критическое значение статистики находятся из условия Ф(tkp)=1-2*0,05=0,9,откуда по таблице приложений tkp =t0,9=1,64,а при конкурирующей гипотезе Н2-из условия Ф(tkp)=1-0,05=0,95, откуда по таблице tkp=t0,95=1,96. Так как фактически наблюдаемое значение t=4,00 больше критического значения tkp(при любой из взятых конкурирующих гипотез), то гипотеза Но отвергается, т.е. на 5%-ном уровне значимости можно сделать вывод, что новая технология позволяет повысить среднюю выработку рабочих. Пример Произведены две выборки урожая пшеницы : при своевременной уборке урожая и уборке с некоторым опозданием .В первом случае при наблюдении 8 участков выборочная средняя урожайность составила 16,2ц/га, а среднее квадратическое отклонение - 3,2 ц/га; во втором случае при наблюдении 9 участков те же характеристики равнялись соответственно 13,9ц/га и 2,1 ц/га. На уровне значимости α.= 0,05 выяснить влияние своевременности уборки урожая на среднее значение урожайности. Решение. Проверяемая гипотеза Но: 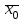 = = 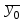 , т.е. средние значения урожайности при своевременной уборке урожая и с некоторым опозданием равны. В качестве альтернативной гипотезы берем гипотезу Н1: , т.е. средние значения урожайности при своевременной уборке урожая и с некоторым опозданием равны. В качестве альтернативной гипотезы берем гипотезу Н1: 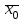 > >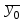 , принятие которой означает существенное влияние на урожайность сроков уборки. , принятие которой означает существенное влияние на урожайность сроков уборки.Фактически наблюдаемое значение статистики критерия 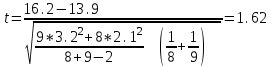 Критическое значение статистики для односторонней области определяется при числе степеней свободы к= 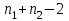 = 9+ 8-2= 15 из условия Ө(t,к) = 1—2*0,05 = 0,9, откуда по таблице приложений t0,9;15= 1,75. Так как t = 1,62 < t0,9;15=1,75, то гипотеза Но принимается. Это означает, что имеющиеся выборочные данные на 5%-ном уровне значимости не позволяют считать, что некоторое запаздывание в сроках уборки оказывает существенное влияние на величину урожая. Еще раз подчеркнем, что это не означает безоговорочную верность гипотезы Но. Вполне возможно, что только незначительный объем выборки позволил принять эту гипотезу, а при увеличении объемов выборки (числа отобранных участков) гипотеза Но будет отвергнута. = 9+ 8-2= 15 из условия Ө(t,к) = 1—2*0,05 = 0,9, откуда по таблице приложений t0,9;15= 1,75. Так как t = 1,62 < t0,9;15=1,75, то гипотеза Но принимается. Это означает, что имеющиеся выборочные данные на 5%-ном уровне значимости не позволяют считать, что некоторое запаздывание в сроках уборки оказывает существенное влияние на величину урожая. Еще раз подчеркнем, что это не означает безоговорочную верность гипотезы Но. Вполне возможно, что только незначительный объем выборки позволил принять эту гипотезу, а при увеличении объемов выборки (числа отобранных участков) гипотеза Но будет отвергнута.Пример Имеются следующие данные об урожайности пшеницы на 8 опытных участках одинакового размера (ц/га): 26,5; 26,2; 35,9; 30,1; 32,3; 29,3; 26,1; 25,0. Есть основание предполагать, что значение урожайности третьего участка х*=35,9 зарегистрировано неверно. Является ли это значение аномальным (резко выделяющимся) на 5%-ном уровне значимости? Решение. Исключив значение х*= 35,9, найдем для оставшихся наблюдений 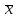 =27,93 (ц/га) и s= 2,67 (ц/га). Фактически наблюдаемое значение =27,93 (ц/га) и s= 2,67 (ц/га). Фактически наблюдаемое значение 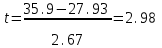 , больше табличного tкр= t1-2α;n-1= t0,9;6=1.94, следовательно, значение х* = 35,9 является аномальным, и его следует отбросить. , больше табличного tкр= t1-2α;n-1= t0,9;6=1.94, следовательно, значение х* = 35,9 является аномальным, и его следует отбросить.Пример. Контрольную работу по высшей математике по индивидуальным вариантам выполняли студенты двух групп первого курса. В первой группе было предложено 105 задач, из которых верно решено 60, во второй группе из 140 предложенных задач верно решено 69. На уровне значимости 0,02 проверить гипотезу об отсутствии существенных различий в усвоении учебного материала студентами обеих групп. Решение. Имеем гипотезу Но: р1 = р2 = р, т.е. доли решенных задач студентами первой и второй групп равны. В качестве альтернативной возьмем гипотезу Н1 р1 ≠р2. При справедливости гипотезы Но наилучшей оценкой р будет в соответствии с равенством р = 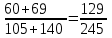 = 0,527. Выборочные доли решенных задач для каждой группы w1= = 0,527. Выборочные доли решенных задач для каждой группы w1=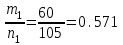 и w2= и w2=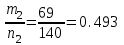 . . Статистика критерия по формуле t= . . Статистика критерия по формуле t=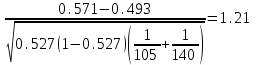 При конкурирующей гипотезе Н1 выбираем критическую двустороннюю область, границы которой определяем из условия: Ф(tкр)=1-0,02=0,98, откуда по таблице приложений tкр=t0.98=2.33 Фактическое значение критерия меньше критического, т.е. t Пример. По условию предыдущего примера на уровне значимости α = 0,05 выяснить, можно ли считать, что различия в усвоении учебного материала студентами четырех групп первого курса существенны. Дополнительные условия: для третьей группы m3=63,n3= 125, для четвертой группы m4 = 105, n4 = 160. Решение. Выдвигаем гипотезу Но: р1 =р2=р3=р4=р или рi = р(i = 1, 2, 3, 4). т.е. доли решенных задач всех групп равны. Вычислим по формуле (10.12) оценку 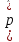 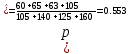 Выборочные доли решенных задач для каждой группы wl== 0,571,w2=0,499 (см. пример 10.4), w3 = 63/125 = 0,504, w4 = 105/160 = 0,656. Статистика критерия по формуле (10.11) 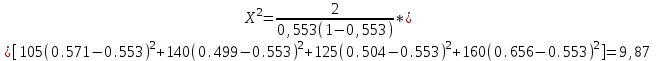 По таблице приложений 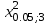 = 7,82. Так как х2 > = 7,82. Так как х2 >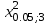 (9,87 >7,82), то гипотеза Но отвергается, т.е. различие в усвоении учебного материала студентами четырех групп значимо или существенно на уровне α =0,05. (9,87 >7,82), то гипотеза Но отвергается, т.е. различие в усвоении учебного материала студентами четырех групп значимо или существенно на уровне α =0,05.Пример. На двух токарных станках обрабатываются втулки. Отобраны две пробы: из втулок, сделанных на первом станке, n1=15шт., на втором станке –n2=18шт.По данным этих выборок рассчитаны выборочные дисперсии 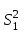 = 8,5 (для первого станка) и = 8,5 (для первого станка) и 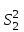 = 6,3 (для второго станка). Полагая, что размеры втулок подчиняются нормальному закону распределения, на уровне значимости α=0,О5 выяснить, можно ли считать, что станки обладают различной точностью. = 6,3 (для второго станка). Полагая, что размеры втулок подчиняются нормальному закону распределения, на уровне значимости α=0,О5 выяснить, можно ли считать, что станки обладают различной точностью.Решение. Имеем нулевую гипотезу Но: 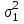 = = 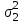 , т.е. дисперсии размера втулок, обрабатываемых на каждом станке, равны. Возьмем в качестве конкурирующей гипотезу Н1: , т.е. дисперсии размера втулок, обрабатываемых на каждом станке, равны. Возьмем в качестве конкурирующей гипотезу Н1: 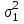 > >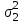 (дисперсия больше для первого станка). Статистика критерия (в качестве дисперсии (дисперсия больше для первого станка). Статистика критерия (в качестве дисперсии 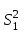 , стоящей в числителе, берут бльшую из двух дисперсий — это дает возможность, учитывая свойства F-распределения, в два раза сократить объем его табличных значений): , стоящей в числителе, берут бльшую из двух дисперсий — это дает возможность, учитывая свойства F-распределения, в два раза сократить объем его табличных значений):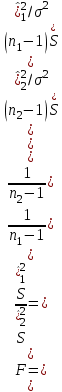 По таблице приложений критическое значение F-критерия на уровне значимости α= 0,05 при числе степеней свободы к 1 = n1-1=14 и к 2 = n2-1=17, т.е. F0.05;14;17 = 2,33. Так как F < F0.05;14;17 то гипотеза Нo не отвергается, т.е. имеющиеся данные не позволяют считать, что станки обладают различной точностью. Замечание. Если в качестве конкурирующей гипотезы в данной задаче взять гипотезу Н1:  ≠ ≠ то, как уже отмечено выше (см. рис. 10.5, в), следовало взять двустороннюю критическую область и найти Fα/2;k1;k2 и F1-α/2;k1;k2 соответственно из условий P(F < F1-α/2;k1;k2 )=α/2 и Р(F > Fα/2;k1;k2)=α/2. При этом гипотеза Но отвергается, если полученное значение F < F1-α/2;k1;k2 или F > Fα/2;k1;k2. то, как уже отмечено выше (см. рис. 10.5, в), следовало взять двустороннюю критическую область и найти Fα/2;k1;k2 и F1-α/2;k1;k2 соответственно из условий P(F < F1-α/2;k1;k2 )=α/2 и Р(F > Fα/2;k1;k2)=α/2. При этом гипотеза Но отвергается, если полученное значение F < F1-α/2;k1;k2 или F > Fα/2;k1;k2.Однако непосредственно по таблицам F-критерия можно найти лишь правую границу Fα/2;k1;k2. (бoльшую единицы), левую же границу F1-α/2;k1;k2 (меньшую единицы) находят из соотношения, доказанного для F-критерия: F1-α/2;k1;k2 =  В данном случае при α= 0,05 в задаче следовало найти F0,025;14;17 иF0.975;14;17 =  На практике обычно используется таблица значений F-критерия (см. табл. VI приложений), в которой приведены значения, F0.05;k1;k2 и F0,01;k1;k2 .Это позволяет осуществлять проверку гипотезы Но на 5%- ном и 1%-ном уровнях значимости при использовании односторонней критической области, и на 10%-ном и 2%-ном уровнях значимости при двусторонней критической области. Пример. По условию предыдущего примера на уровне значимости α = 0 05 выяснить, можно ли считать, что станки обладают различной точностью, если имеются 4 токарных станка и отобраны соответственно четыре пробы объемов: n1= 15; n2= 18; n3 = 25; n4 = 32, а выборочные дисперсии размеров втулок равны соответственно: 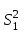 =8,5; =8,5; 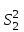 = 6,3; = 6,3; 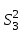 =9,3; =9,3; 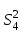 = 5,8. = 5,8.Решение. Имеем нулевую гипотезу Но:  = =  = =  = = = =  или или  = =  , (i=1, 2, 3, 4) По формуле (10.14) найдем исправленные выборочные дисперсии размеров втулок: , (i=1, 2, 3, 4) По формуле (10.14) найдем исправленные выборочные дисперсии размеров втулок: ; ; 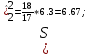 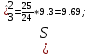 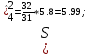 Оценка средней арифметической дисперсии 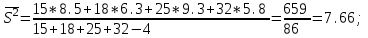 Статистика критерия равна: 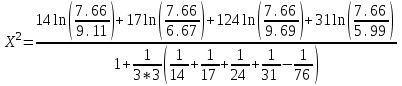 По таблице приложений Х 2 0.05;3 =7,82. Так как X2 < Х 2 0.05;3 (1,87 <7,82), то гипотеза Но не отвергается, т.е. имеющиеся данные не позволяют считать, что рассматриваемые станки обладают различной точностью. Пример. На основании сделанного прогноза средняя дебиторская задолженность однотипных предприятий региона должна составить а0 = 120 ден.ед. Выборочная проверка 10 предприятий дала среднюю задолженность 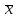 = 135 ден.ед., а среднее квадратическое отклонение задолженности S= 20 ден. ед. На уровне значимости 0,05: = 135 ден.ед., а среднее квадратическое отклонение задолженности S= 20 ден. ед. На уровне значимости 0,05:а) Выяснить, можно ли принять данный прогноз; б) найти мощность критерия, использованного в п. а); в) определить минимальное число предприятий, которое следует проверить, чтобы обеспечить мощность критерия 0,975. Решение. а) Проверяемая гипотеза Но: 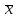 0 = а0 =120. В качестве альтернативной возьмем гипотезу Н1: 0 = а0 =120. В качестве альтернативной возьмем гипотезу Н1: 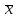 0= а1 =135. Так как генеральная дисперсия 0= а1 =135. Так как генеральная дисперсия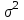 неизвестна, то используем t-критерий Стьюдента. Статистика критерия неизвестна, то используем t-критерий Стьюдента. Статистика критерия 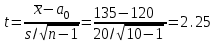 Критическое значение статистики t1-2*0.05;10-1=t0.9;9=1.83 Так как 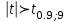 (2.25>1,8З), то гипотеза Нo отвергается, т.е.на 5%-ном уровне значимости сделанный прогноз должен быть отвергнут. (2.25>1,8З), то гипотеза Нo отвергается, т.е.на 5%-ном уровне значимости сделанный прогноз должен быть отвергнут.б) Так как a1 = 135 > а0 = 120, то критическая область правосторонняя и критическое значение выборочной средней 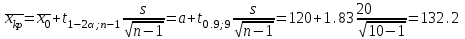 (ден. ед.), (ден. ед.),т.е. критическая область значений для 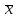 есть интервал (132,2+∞). Мощность критерия (см. § 10.2) равна вероятности Р отвергнуть гипотезу Но, когда верна гипотеза Н1, т.е. есть интервал (132,2+∞). Мощность критерия (см. § 10.2) равна вероятности Р отвергнуть гипотезу Но, когда верна гипотеза Н1, т.е.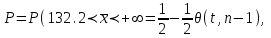 Где 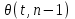 — функция, выражающая вероятность попадания случайной величины, имеющей t-распределение Стьюдента, на отрезок (—t, t) (аналогична функции Лалласа для нормального распределения (см. § 9.7); — функция, выражающая вероятность попадания случайной величины, имеющей t-распределение Стьюдента, на отрезок (—t, t) (аналогична функции Лалласа для нормального распределения (см. § 9.7);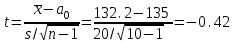 По табл. IV приложений1 θ (—0,42; 9) =-θ (0,42; 9) ≈-0,31. Итак P 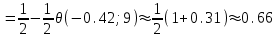 в) Воспользуемся решением примера в котором формула объема выборки была получена для случая нормального закона распределения, когда известна генеральная дисперсия 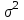 . Так как у нас . Так как у нас 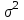 не известна, а известна лишь ее выборочная оценка S2,то статистика критерия не известна, а известна лишь ее выборочная оценка S2,то статистика критерия 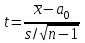 , имеет t-распределение Стьюдента (см. табл. 10.2), и соответствующая скорректированная формула для n примет вид: , имеет t-распределение Стьюдента (см. табл. 10.2), и соответствующая скорректированная формула для n примет вид:n= 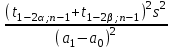 При α= 0,05, β = 0,025 (ибо по условию мощность критерия 1 —β = 0,975), α0 = 120, α1 = 135,s = 20 получим: n 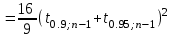 (*) (*)Так как правая часть равенства сама зависит от неизвестного значения n, то n находится приближенно подбором. Так, при n = 20, n = 30, равенство (*) не выполняется (например, при n = 20 20 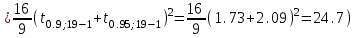 ,а при n =25 ,а при n =25 25 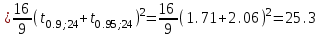 Следовательно, необходимо проверить 25 предприятий. Аналогично проверяются и другие гипотезы о числовых значениях параметров в соответствии с критериями проверки, приведенными в табл. 10.2. Пример 10.9. По данным примера 9.10 на уровне значимости α≈ 0,05 проверить гипотезу о том, что средняя выработка рабочих всего цеха равна 121%. Р е ш е н и е. Проверяемая гипотеза Н0:  = 121(%). Конкурирующая гипотеза Н1: = 121(%). Конкурирующая гипотеза Н1: ≠ 121. В примере 9.10 с надежностью γ ≈ 1-0,05=0,95 построен доверительный интервал для ≠ 121. В примере 9.10 с надежностью γ ≈ 1-0,05=0,95 построен доверительный интервал для : 117,33≤ : 117,33≤  ≤ 121,07. Так как значение а=121 принадлежит этому интервалу, то гипотеза Н0 не отвергается, т.е. имеющиеся данные не противоречат предположению о том, что средняя выработка рабочих равна 121%. ≤ 121,07. Так как значение а=121 принадлежит этому интервалу, то гипотеза Н0 не отвергается, т.е. имеющиеся данные не противоречат предположению о том, что средняя выработка рабочих равна 121%.Пример 10.10. По данным примера 9.11 на уровне значимости α = 0,05 проверить гипотезу о том, что доля нестандартных деталей во всей партии равна 12%. Р е ш е н и е. Проверяемая гипотеза Н0: р = 0,12 (или 12%). Конкурирующая гипотеза Н1: р≠0,12. В примере 9.11 с надежностью γ ≈ 1-0,05=0,95 построен доверительный интервал для р: 0,044≤ р ≤0,116. Так как значение р0= 0,12 не принадлежит этому интервалу, то ва уровне значимости α = 0,05 гипотеза Н0 отвергается, т.е. имеющиеся данные не позволяют считать, что в партии находится 12% нестандартных деталей. Пример 10.11. По данным примера 9.17 на уровне значимости α = 0,1 проверить гипотезу о том, что среднее квадратическое отклонение суточной выработки работниц равно 20 м/ч. Р е ш е н и е. Проверяемая гипотеза Но:  = 202 =400.Конкурирующая гипотезаН1: = 202 =400.Конкурирующая гипотезаН1: = 400. В примере 9.17 с надежностью γ =1—0,1=0,9 получен доверительный интервал для = 400. В примере 9.17 с надежностью γ =1—0,1=0,9 получен доверительный интервал для  : 157,3≤ : 157,3≤ ≤468,9. Так как значение ≤468,9. Так как значение  0= 400 принадлежит этому интервалу, то на уровне значимости α= 0,1 гипотеза Но не отвергается, т.е. имеющиеся данные не противоречат предположению о том, что среднее квадратическое отклонение суточной выработки работниц равно 20 м/ч. 0= 400 принадлежит этому интервалу, то на уровне значимости α= 0,1 гипотеза Но не отвергается, т.е. имеющиеся данные не противоречат предположению о том, что среднее квадратическое отклонение суточной выработки работниц равно 20 м/ч. |
