Практические задания (10). Проверяемое задание Определение противопожарных разрывов между объектами различного назначения
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
Образец выполнения задания 6Пример и методика расчета Расчет огнестойкости конструкций целесообразно начинать с прочностной части, т. е. с определения критических напряжений и, следовательно, критической температуры конструкции. Далее производят теплотехнический расчет, в результате чего находят время прогрева конструкции до критической температуры, т. е. ее предел огнестойкости. Для изгибаемых элементов (рис. 6.1) критическое состояние их сечений определяет формула 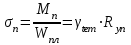 , (6.1) , (6.1)где 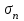 – нормальные напряжения в сечении конструкции, Н/м2 или Па; – нормальные напряжения в сечении конструкции, Н/м2 или Па; 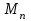 – изгибающий момент от нормативной нагрузки в сечении конструкции, Н.м; – изгибающий момент от нормативной нагрузки в сечении конструкции, Н.м; 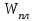 – пластический момент сопротивления сечения, м3; – пластический момент сопротивления сечения, м3; 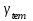 – температурный коэффициент снижения сопротивления стали; – температурный коэффициент снижения сопротивления стали; 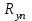 – нормативное сопротивление стали по пределу текучести, Па. – нормативное сопротивление стали по пределу текучести, Па.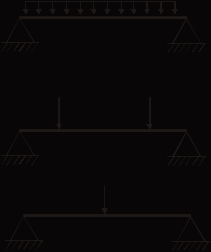 Рис. 6.1. Типовые схемы нагружения балок Пластический момент сопротивления сечения равен 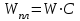 , (6.2) , (6.2)где 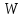 – момент сопротивления сечения, м3; – момент сопротивления сечения, м3; 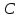 – коэффициент развития пластических деформаций. – коэффициент развития пластических деформаций.При расчетах пределов огнестойкости значения коэффициента С следует принимать равными: для прямоугольного сечения – 1,5; для двутавров и швеллеров – 1,17; для труб – 1,25. Рассмотрим пример (рис. 6.2). Металлическая шарнирноопертая балка пролетом l = 6 м. Сечение – двутавр № 36 по ГОСТ 8239-89 (горячекатаный с уклоном граней полок). Двутавр изготовлен из стали С245, Rуп = 245 МПа. Нагрузка на балку – центрально симметричная равномерно распределенная – qн = 15 кН/м. 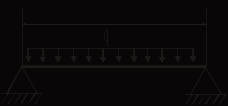 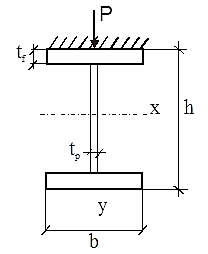 Рис. 6.2. Геометрические характеристики и схема нагружения двутавровой балки Таблица 6.2 Геометрические характеристики сечения двутавра № 36 по ГОСТ 8239
Для того чтобы найти предел огнестойкости заданной нагруженной металлической балки, необходимо найти 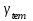 – температурный коэффициент снижения сопротивления стали. – температурный коэффициент снижения сопротивления стали.Температурный коэффициент снижения прочности стали 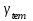 определяется из формул 6.1, 6.2: определяется из формул 6.1, 6.2: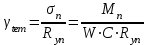 (6.3). (6.3).Изгибающий момент от нормативной нагрузки в сечении конструкции 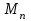 находится в зависимости от схемы опирания конструкции и схемы приложения нагрузки. Для случая равномерно нагруженной шарнирноопертой балки (см. рис. 6.2) получим: находится в зависимости от схемы опирания конструкции и схемы приложения нагрузки. Для случая равномерно нагруженной шарнирноопертой балки (см. рис. 6.2) получим: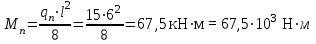 . .Предел текучести определяется маркой стали, из которой сделана конструкция, и по условию задачи составляет Rуп = 245 МПа. Для двутавра значение коэффициента C = 1,17. Момент сопротивления сечения для несимметричного сечения берется в зависимости от схемы приложения нагрузки. Например, для двутавра при заданной в условиях задачи схеме приложения нагрузки (см. рис. 6.2) получим: 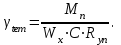 (6.4) (6.4)При другой схеме приложения нагрузки (рис. 6.3): 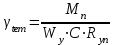 . (6.5) . (6.5)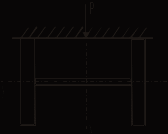 Рис. 6.3. Схема нагружения двутавровой балки В нашем случае имеем: 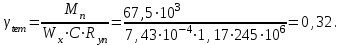 Далее определяем критическую температуру. Для растянутых элементов и изгибаемых элементов критическая температура определяется в зависимости от найденного значения 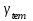 : :при 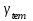 < 0,6: < 0,6: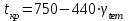 ; ; при 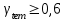 : :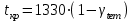 . (6.6) . (6.6)Таким образом, получим 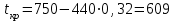 оС. оС.Далее определим приведенную толщину сечения балки: 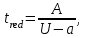 (6.7) (6.7)где А – площадь сечения без учета скруглений, мм2; U – обогреваемая часть периметра сечения, мм, 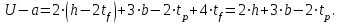 (6.8) (6.8)После подстановки данных получим: 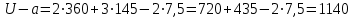 мм; мм;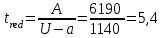 мм. мм.Зная критическую температуру прогрева металлической конструкции 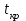 на основе приведенной толщины сечения на основе приведенной толщины сечения 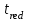 , время достижения предела огнестойкости , время достижения предела огнестойкости 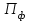 определяется по табл. 6.3 методом интерполяции. определяется по табл. 6.3 методом интерполяции.Таблица 6.3 Температура прогрева незащищенных стальных пластин
Рассмотрим порядок интерполяции. Выбирают в таблице 6.3 значение 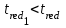 и определяют время при этом значении: и определяют время при этом значении: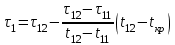 , (6.9) , (6.9)где 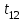 и и 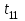 – ближайшие к – ближайшие к 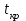 табличные значения температуры. табличные значения температуры.Выбирают в табл. 6.3 также значение 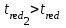 и определяют время при этом значении: и определяют время при этом значении: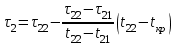 . (6.10) . (6.10)В нашем случае 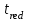 =5,4 мм, а =5,4 мм, а 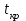 =609 оС. Подставляем значения в интерполяционные формулы: =609 оС. Подставляем значения в интерполяционные формулы: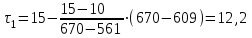 мин; мин;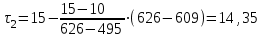 мин. мин.Используя найденные значения, определяем предел огнестойкости: 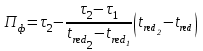 , (6.11) , (6.11)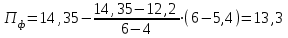 мин. мин. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
