лабораторная работа по моделированию. лаба 2. Псковский государственный университет
 Скачать 137.1 Kb. Скачать 137.1 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ПСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Институт инженерных наук Кафедра информационно-коммуникационных технологий ОТЧЁТ ПО ПРАКТИКУМУ ОСНОВЫ МОДЕЛИРОВАНИЯ Лабораторная работа 2. Вариант 3 Выполнил: Ильин А.А. Группа: 0432-03 Проверил: Миронов Т.С. Псков 2022 Задание 2.1.Точечные оценки математического ожидания. Точечные оценки дисперсии.Необходимо найти состоятельные несмещенные оценки математического ожидания М[] и дисперсии D[] случайной величины по приведенным в задании выборочным значениям 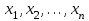 . .Ввели выборку с клавиатуры: 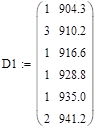 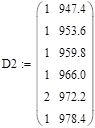 Далее необходимо определить объем выборки:  Следует найти точечную оценку математического ожидания М[]. Математическое ожидание это: одно из важнейших понятий в математической статистике и теории вероятностей, характеризующее распределение значений или вероятностей случайной величины. Обычно выражается как средневзвешенное значение всех возможных параметров случайной величины. Затем находим несмещенную среднеквадратичную оценку дисперсии Dx и состоятельную смещенную оценку дисперсии Dx1: 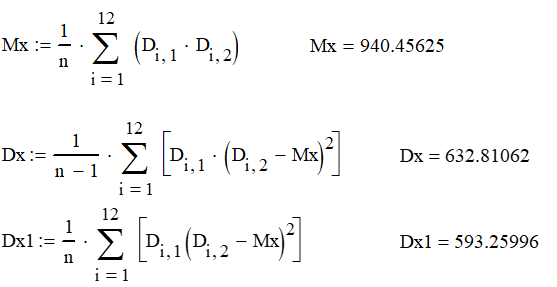 Несмещенная оценка дисперсии, это такая оценка, которая равна оцениваемому параметру. Также является исправленной выборочной дисперсией. В свою очередь, смещенной оценкой генеральной дисперсии служит выборочная дисперсия. Выборочной дисперсией - называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения. Вывод: данная выборка характеризуется такими значениями: математическое ожидание Mx = 940.45625, несмещенная среднеквадратичная оценка дисперсии Dx = 632.81062 и смещенная оценка дисперсии Dx1 = 593.25996. После вычислений видно что несмещенная оценка даёт больший результат, по сравнению со смещенной. Задание 2.2.Точечная оценка вероятности события.Создадим несколько выборок значений случайной величины, имеющий распределение Бернулли с заданным значением параметра р = 0,3. (распределение Бернулли - это дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи). Вычисление для каждого значения п точечные оценки 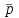 вероятности р. вероятности р. , где , где 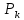 – вероятность биномиального распределения. – вероятность биномиального распределения.rbinom(m, n, p) — Возвращает вектор m случайных чисел, имеющих биномиальное распределение. 0 Биномиальное распределение – это распределение случайных величин, количества «успехов» в последовательности из независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна. Распределение Бернулли моделирует случайный эксперимент, когда заранее известна вероятность успеха или неудачи. График зависимости величины 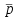 от объема выборки выглядит так: от объема выборки выглядит так: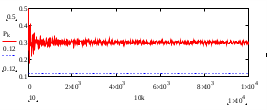 Далее вычисляется значение отклонения, равное 4% от оптимального значения: 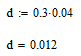 С учетом отклонения график выглядит так: 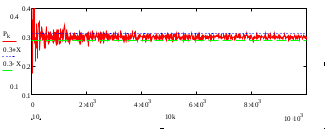 Вывод: на втором графике видно, что при объёме выборки 1000 точечная оценка попадает в пределы четырехпроцентного отклонения. Отклонения становятся несущественными с увеличением выборки. Также на скриншоте показан график зависимости точечной оценки от объема выборки (первый график) и из него следует вывод: Точность оценки напрямую зависит от объема выборки, и с его увеличением точность так же увеличивается. Задание 2.3.Точечная оценка параметров равномерного распределения.Необходимо смоделировать несколько выборок разного объема значений случайной величины, имеющей равномерное распределение на отрезке [0; θ] при значении θ = 1,5. Для этого нужно для каждого значения п вычислить точечные оценки T1k и T3k и их отклонение p1 и p3: При k= 8  При k=17 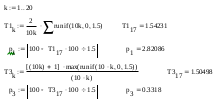 Точечная оценка в мат. статистике – это число, оцениваемое на основе наблюдений, предположительно близкое к оцениваемому параметру. Функция runif(m, a ,b) - Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. a < b. График зависимости точечных оценок T1k и T3k от объема выборки: 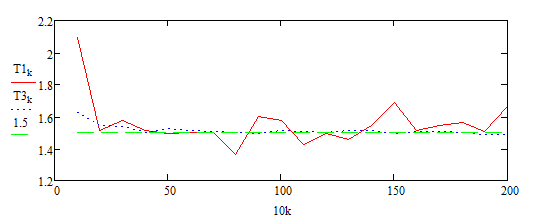 Вывод: как видно из приведенных выше вычислений, значение =1.5 при объеме выборки 8 оценка Т1 больше выборки Т3, в свою очередь, при объеме выборки 17 оценка Т1 так же больше выборки Т3 |
