|
|
рабочая тетрадь 5. Рабочая тетрадь 5. Рабочая тетрадь 5
Рабочая тетрадь № 5
Составление логических формул позволяет решать определённые классы задач, но зачастую получившаяся запись неудобна, сложна или непригодна для дальнейшего анализа или проведения исследований. Поэтому логические формулы необходимо уметь упрощать. Методики «упрощений» делятся на два класса:
1) приведение исходной логической формулы к более компактному виду, т.е. уменьшение числа логических операций, которые нужно выполнить;
2) приведение исходной логической формулы к одному из стандартных специальных видов, удобных для вычисления и анализа.
|
1. Теоретический материал
|
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, 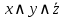 является простой конъюнкцией. является простой конъюнкцией.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение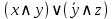 является ДНФ. Для одной и той же логической формулы можно получить несколько разных по составу ДНФ. Принято среди всех этих ДНФ выделять одну «совершенную» форму, которая всегда существует в единственном виде для конкретной логической формулы. является ДНФ. Для одной и той же логической формулы можно получить несколько разных по составу ДНФ. Принято среди всех этих ДНФ выделять одну «совершенную» форму, которая всегда существует в единственном виде для конкретной логической формулы.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение 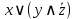 является ДНФ, но не СДНФ. является ДНФ, но не СДНФ.
Выражение 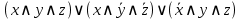 является СДНФ. является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).
Например, выражение 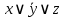 – простая дизъюнкция. – простая дизъюнкция.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций.
Например, выражение 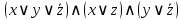 – КНФ. – КНФ.
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 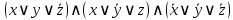 является СКНФ. является СКНФ.
Простейший (но весьма громоздкий) способ построения дизъюнктивных и конъюнктивных нормальных форм для булевых функций состоит в использовании эквивалентных преобразований, основанных на следующих тождествах:
№
|
Название тождества
|
Тождество
|
|
Двойное отрицание
|
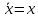
|
|
Коммутативность
|
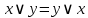
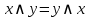
|
|
Ассоциативность
|
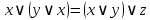
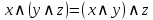
|
|
Дистрибутивность
|
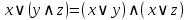
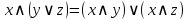
|
|
Законы де Мограна
|
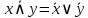
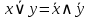
|
|
Свойства констант
|
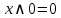
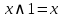
|
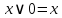
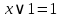
|
|
Свойства отрицаний
|
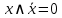
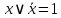
|
|
Идемпотентность
|
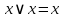
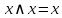
|
|
Поглощение
|
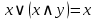
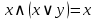
|
|
Склеивание (расщепление)
|
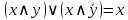
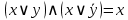
|
|
Операция «импликация»
|
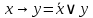
|
|
Операция «эквивалентность»
|
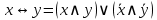
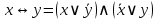
|
|
Операция «исключающее ИЛИ»
|
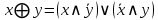
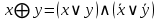
|
|
Операция «стрелка Пирса»
|
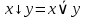
|
|
Операция «штрих Шеффера»
|
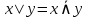
|
Для получения ДНФ или КНФ используется следующий алгоритм:
1) все логические операции выражаются через ∧, ∨, ¬ (тождества 11-15);
2) отрицания над логическими выражениями преобразуются по законам де Моргана (тождество 5) так, чтобы все отрицания относились только к переменным;
3) для получения ДНФ и КНФ все скобки раскрываются закону дистрибутивности:
3.1) для получения ДНФ – по первому закону дистрибутивности (тождество 4, верхняя формула);
3.2) для получения КНФ – по второму закону дистрибутивности (тождество 4, нижняя формула).
Напомним названия, обозначения и таблицы истинности основных логических операций:
1) 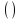 – группирующие скобки; – группирующие скобки;
2) 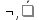 – отрицание; – отрицание;
3) 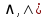 – конъюнкция; логическое «И»; логическое умножение; – конъюнкция; логическое «И»; логическое умножение;
4) 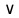 – дизъюнкция; логическое «ИЛИ»; логическое сложение; – дизъюнкция; логическое «ИЛИ»; логическое сложение;
5)  – исключающее «ИЛИ»; сложение по модулю два; – исключающее «ИЛИ»; сложение по модулю два;
6) 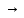 – импликация; – импликация;
7) 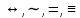 – эквивалентность; эквиваленция; – эквивалентность; эквиваленция;
8) 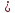 – штрих Шеффера; логическое «И-НЕ»; – штрих Шеффера; логическое «И-НЕ»;
9) 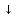 – стрелка Пирса; логическое «ИЛИ-НЕ»; – стрелка Пирса; логическое «ИЛИ-НЕ»;
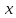
|
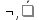
|
0
|
1
|
1
|
0
|
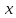
|
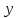
|
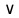
|
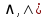
|
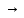
|
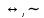
|

|
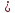
|
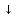
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
|
2. Пример
|
Задача:
|
|
Установить характер истинности формулы
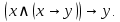
|
Решение:
|
|
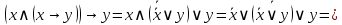
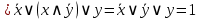
|
Ответ:
|
|
1
|
Задача:
|
|
Упростить формулу
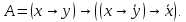
|
Решение:
|
|
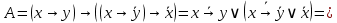
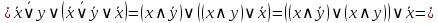
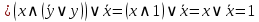
|
Ответ:
|
|
1
|
Задача:
|
|
Найти ДНФ, КНФ для функции
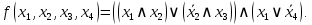
|
Решение:
|
|
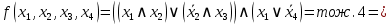
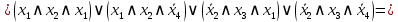
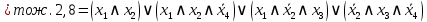
Последнее выражение находится в ДНФ.
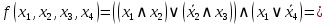
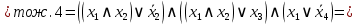
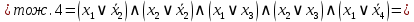
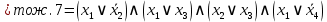
Последнее выражение находится в КНФ.
|
Задача:
|
|
С помощью эквивалентных преобразований приведите формулу к ДНФ и КНФ
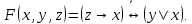
|
Решение:
|
|
Сначала приведём логическую формулу 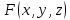 к ДНФ. к ДНФ.
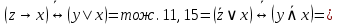
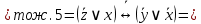
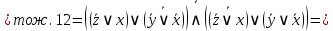
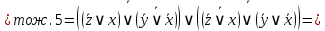
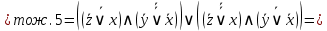
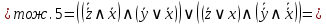
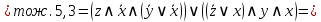
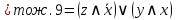
Для приведения формулы 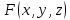 к КНФ удобнее, в данном случае, воспользоваться её ДНФ. к КНФ удобнее, в данном случае, воспользоваться её ДНФ.
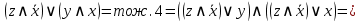
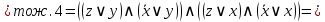
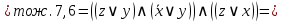
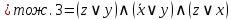
|
Ответ:
|
|
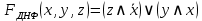
| |
|
|
 Скачать 489.08 Kb.
Скачать 489.08 Kb.