|
|
рабочая тетрадь 5. Рабочая тетрадь 5. Рабочая тетрадь 5
3. Задания
|
1.
|
Задача:
|
|
Доказать равносильность с помощью эквивалентных преобразований:
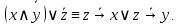
|
Решение:
|
|
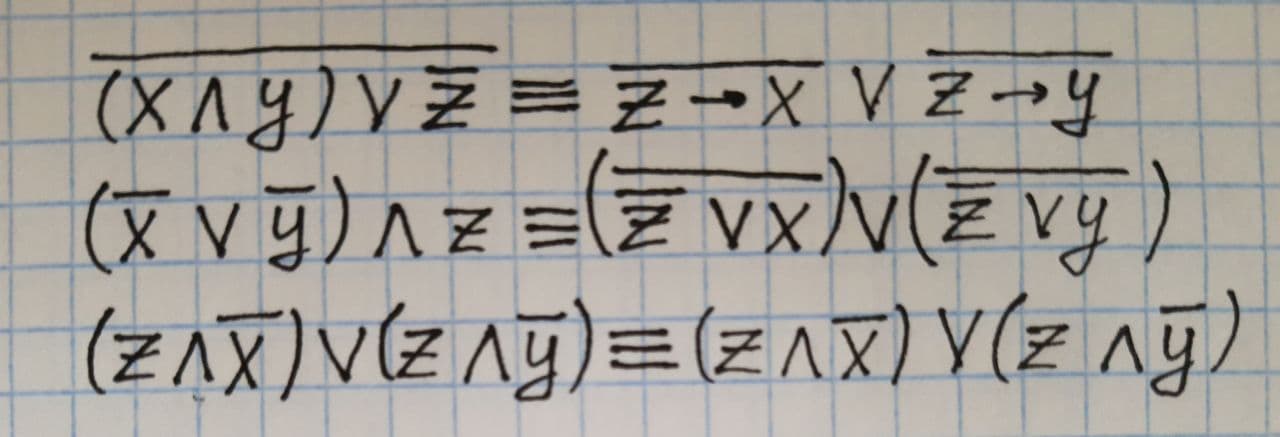
|
Ответ:
|
|
|
2.
|
Задача:
|
|
С помощью таблиц истинности доказать равносильность:
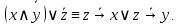
|
Решение:
|
|

|
Ответ:
|
|
|
3.
|
Задача:
|
|
С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ:
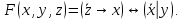
|
Решение:
|
|
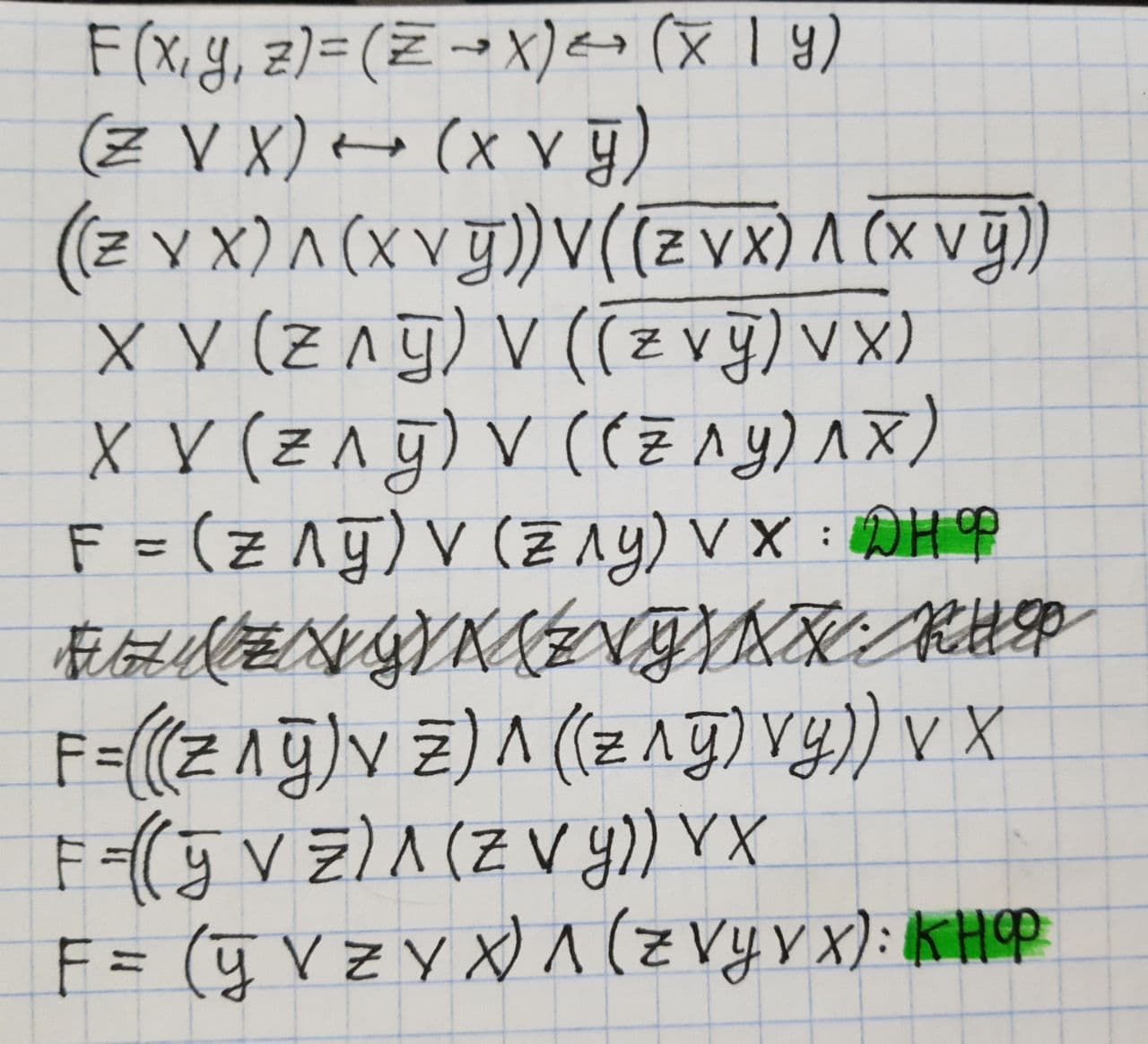
|
Ответ:
|
|
|
4.
|
Задача:
|
|
С помощью равносильных преобразований доказать, что формула:
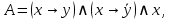
является тождественно ложной.
|
Решение:
|
|
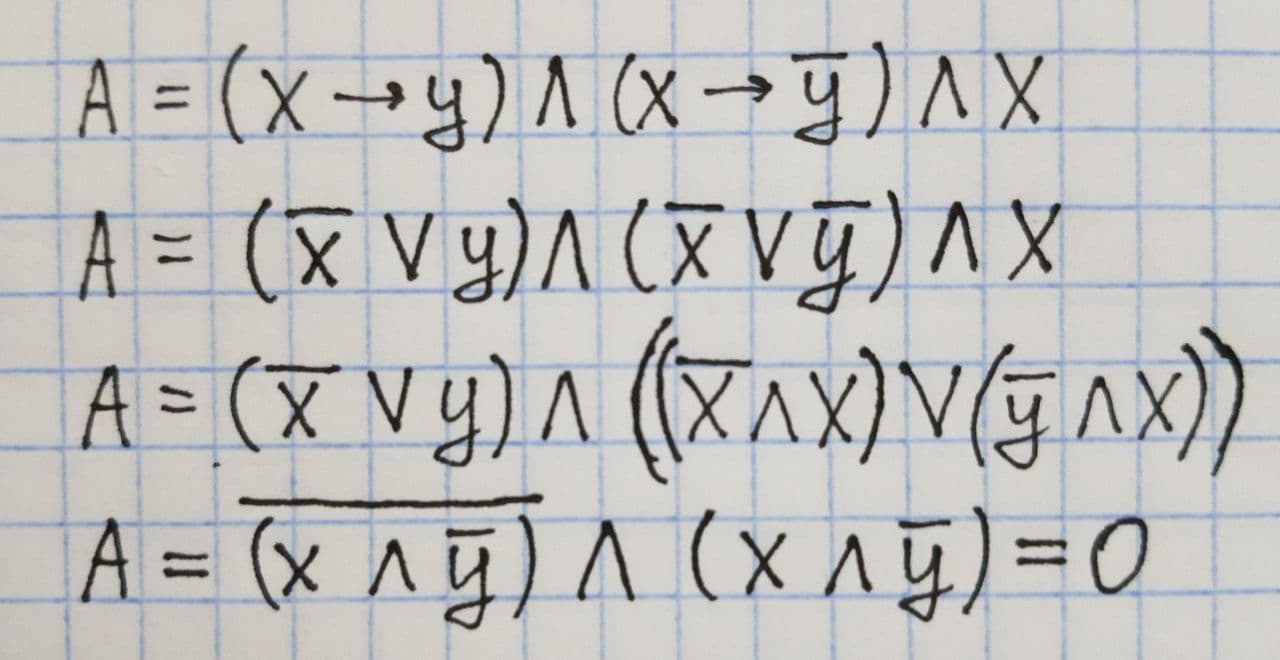
|
Ответ:
|
|
|
1. Теоретический материал
|
Если булева функция не равна тождественно нулю, то ее можно представить в виде СДНФ по ее таблице истинности следующим образом (на примере таблицы истинности для логической функции двух переменных):
Выделяем строки, для которых высказывание оказалось истинным:
№
строки
|
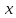
|
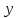
|
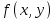
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Заготавливаем следующий шаблон:
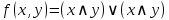
количество круглых скобок равно числу выделенных строк (т.е. каждая скобка соответствует конкретной выделенной строке);
количество логических переменных в круглых скобках, соединённых операциями конъюнкции, равно числу логических переменных в таблице истинности (в нашем случае двум – 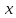 и и 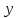 ). ).
Далее в каждой круглой скобке ставим над логической переменной отрицание, если в соответствующей выделенной строке таблицы истинности она имела нулевое значение (ложное значение):
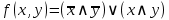
В итоге мы приходим к логическому высказыванию, которое соответствует исходной таблице истинности. Логическое высказывание, записанное в таком виде, называется СДНФ.
|
Если булева функция не равна тождественно единице, то ее можно представить в виде СКНФ по ее таблице истинности следующим образом (на примере таблицы истинности для логической функции двух переменных):
Выделяем строки, для которых высказывание оказалось ложным:
№
строки
|
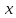
|
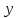
|
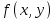
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Заготавливаем следующий шаблон:
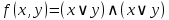
количество круглых скобок равно числу выделенных строк (т.е. каждая скобка соответствует конкретной выделенной строке);
количество логических переменных в круглых скобках, соединённых операциями конъюнкции, равно числу логических переменных в таблице истинности (в нашем случае двум – 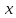 и и 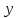 ). ).
Далее в каждой круглой скобке ставим над логической переменной отрицание, если в соответствующей выделенной строке таблицы истинности она имела единичное значение (истинное значение):
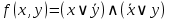
В итоге мы приходим к логическому высказыванию, которое соответствует исходной таблице истинности. Логическое высказывание, записанное в таком виде, называется СКНФ.
|
2. Пример
|
1.
|
Задача:
|
|
Составить для импликации и «сложения по модулю 2» СДНФ и СКНФ.
|
Решение:
|
|
Таблицы истинности функций импликация и суммы по модулю два:
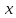
|
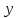
|
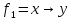
|
|
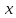
|
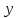
|
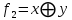
|
0
|
0
|
1
|
|
0
|
0
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
|
1
|
0
|
1
|
1
|
1
|
1
|
|
1
|
1
|
0
|
СДНФ для этих функций:
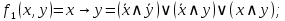
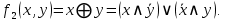
СКНФ для этих функций:
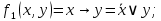
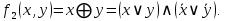
|
Ответ:
|
|
|
2.
|
Задача:
|
|
Найти СДНФ для 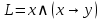 , используя два способа: равносильные преобразования, таблицу истинности. , используя два способа: равносильные преобразования, таблицу истинности.
|
Решение:
|
|
Найдём СДНФ для 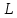 с помощью равносильных преобразований. с помощью равносильных преобразований.
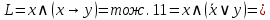
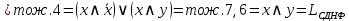
Найдём СДНФ для 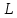 с помощью таблицы истинности: с помощью таблицы истинности:
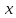
|
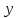
|
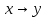
|
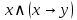 . .
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1) Выделим строки, которые дают «1».
2) Заготовим по числу строк шаблон: 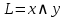 . .
3) Поставим отрицания над переменными, соответствующими значению «0» в таблице истинности (таких нет): 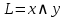 . .
Таким образом, СДНФ:
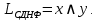
|
|
Ответ:
|
|
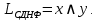
|
3.
|
Задача:
|
|
Найти СКНФ для 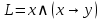 , используя два способа: равносильные преобразования, таблицу истинности. , используя два способа: равносильные преобразования, таблицу истинности.
|
|
Решение:
|
|
Найдём СКНФ для 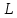 с помощью равносильных преобразований. с помощью равносильных преобразований.
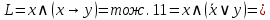
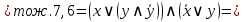
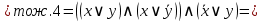
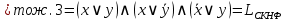
Найдём СКНФ для 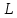 с помощью таблицы истинности: с помощью таблицы истинности:
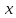
|
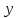
|
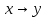
|
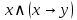 . .
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1) Выделим строки, которые дают «0».
2) Заготовим по числу строк шаблон: 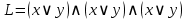 . .
3) Поставим отрицания над переменными, соответствующими значению «1» в таблице истинности : 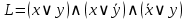 . .
Таким образом, СКНФ:
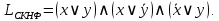
|
Ответ:
|
|
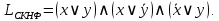
| |
|
|
 Скачать 489.08 Kb.
Скачать 489.08 Kb.