Оптимизация температурного режима в реакторе идеального вытеснения Отчет по лабораторной работе. Работа. Работа Оптимизация температурного режима в реакторе идеального вытеснения Постановка задачи
 Скачать 69.84 Kb. Скачать 69.84 Kb.
|
|
Работа № 1. Оптимизация температурного режима в реакторе идеального вытеснения Постановка задачи: Температура в зоне реакции регулируется теплообменом с поверхностью теплопередачи, температуру которой ТП можно считать постоянной по длине аппарата, а также температурой Т0 жидкости, входящей в аппарат. В этой работе температуры задаются в градусах Цельсия. Таким образом, в нашем распоряжении есть два фактора, влияющих на процесс: Т0 и ТП. Остальные параметры процесса (параметры уравнения Аррениуса для обеих стадий, продолжительность реакции, равная 10 с, удельная поверхность теплообмена fT, теплоемкость cТ и коэффициент теплоотдачи α) заданы для каждого варианта и введены в программу расчета. Цель работы: Необходимо найти такое сочетание температуры на входе и температуры поверхности, при котором степень превращения реагента (равная для этой реакции выходу продукта) окажется максимальной. При этом должно соблюдаться ограничение: ни в одной точке аппарата температура не должна превышать 110°С (383К). При этой температуре происходит вскипание растворителя, нарушающее безопасность и нормальный ход процесса. Ход работы: Для определения положения оптимума необходимо исследовать зависимость отклика системы (выхода продукта A2) от входных параметров (Т0 и ТП). 1. На основе полученных знаний мною была выведена зависимость входных параметров (Всего можно задать 10 режимов) , таким образом чтобы выход продукта был максимально возможный.  2. далее на основе входных параметров была выведена таблица зависимости температуры реакции от времени на основе температур каждого режима 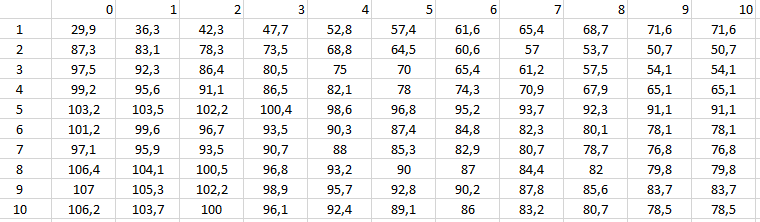 3.После получения результатов были выведены 2 графика на основе пунктов 1 и 2 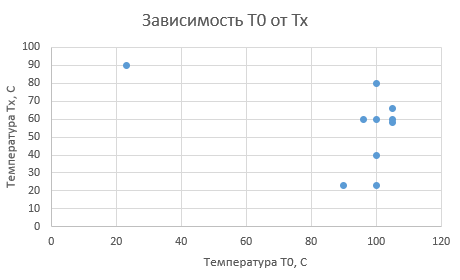 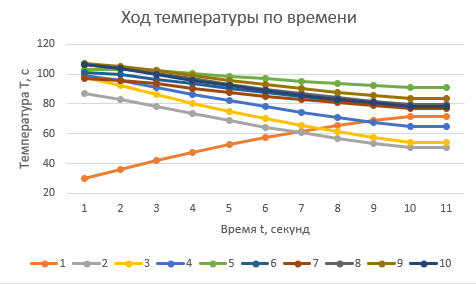 Обсуждение результатов: Для достижения максимального выхода продукта реакции необходимо, чтобы скорость образования целевого продукта была наибольшей. Скорость протекания реакции имеет вид: В начальный момент времени продукт ещё не образовался, то есть его концентрация равна нулю. Следовательно, скорость протекания реакции в начальный момент времени имеет вид: В этом уравнении от температуры зависит только константа скорости реакции. Чем выше константа, тем больше начальная скорость реакции. Константа скорости увеличивается с ростом температуры по уравнению Аррениуса, запишем это уравнение для обеих рассматриваемых констант (с учетом обратной реакции): Чем выше значение энергии активации, тем сильнее влияет температура на константу скорости. А в случае экзотермической реакции, энергия активации обратной реакции больше, чем прямой. Следовательно, температура сильнее влияет на обратную реакцию, и понижение температуры будет сильнее понижать константу скорости обратной реакции, чем константу скорости прямой реакции. Следовательно, целесообразно вначале процесс вести при высокой температуре с целью увеличения скорости прямой реакции до момента накопления достаточного количества целевого продукта. Затем температуру следует снижать, чтобы сместить равновесие в нужную сторону и добиться максимального выхода конечного продукта. Зависимость температуры смеси внутри реактора от времени пребывания аналогичен. Таким образом, температура смеси внутри реактора вначале растет, а далее уменьшается. Чем выше температура жидкости, тем выше экстремум данной зависимости. Максимальная температура жидкости, при которой не возникает угрозы перегрева равна 105°С. Оптимальная температура стенки равна 60°С. Такой температурный режим является оптимальным при заданных условиях и при нем достигается наибольший выход, равный 0,973. Выводы: Наиболее оптимальным условием для проведения заданного процесса является высокая температура вводимой жидкости Т0 и низкая температура стенки Тп. Это приводит к максимальной температуре смеси на входе в реактор и постепенному ее снижению на выходе из реактора, что приводит к максимальной степени превращения реагента и выходу целевого продукта для данной реакции. |
