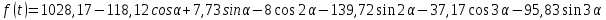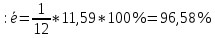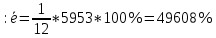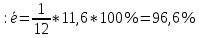Запишем уравнение:

При м=3

t
|
y
|
α
|
3α
|
cos3α
|
sin3α
|
y*cos3α
|
y*sin3α
|
1
|
1000
|
0
|
0
|
1
|
0
|
1000
|
0
|
2
|
850
|
0,523599
|
1,570796
|
6,13E-17
|
1
|
5,21E-14
|
850
|
3
|
930
|
1,047198
|
3,141593
|
-1
|
1,23E-16
|
-930
|
1,14E-13
|
4
|
980
|
1,570796
|
4,712389
|
-1,8E-16
|
-1
|
-1,8E-13
|
-980
|
5
|
970
|
2,094395
|
6,283185
|
1
|
-2,5E-16
|
970
|
-2,4E-13
|
6
|
953
|
2,617994
|
7,853982
|
3,06E-16
|
1
|
2,92E-13
|
953
|
7
|
940
|
3,141593
|
9,424778
|
-1
|
3,68E-16
|
-940
|
3,45E-13
|
8
|
948
|
3,665191
|
10,99557
|
-4,3E-16
|
-1
|
-4,1E-13
|
-948
|
9
|
997
|
4,18879
|
12,56637
|
1
|
-4,9E-16
|
997
|
-4,9E-13
|
10
|
1000
|
4,712389
|
14,13717
|
5,51E-16
|
1
|
5,51E-13
|
1000
|
11
|
1320
|
5,235988
|
15,70796
|
-1
|
6,13E-16
|
-1320
|
8,09E-13
|
12
|
1450
|
5,759587
|
17,27876
|
-2,5E-15
|
-1
|
-3,6E-12
|
-1450
|
сумма
|
12338
|
34,55752
|
103,6726
|
-2,5E-15
|
0
|
-223
|
-575
|
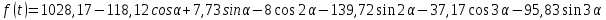
При статистическом прогнозировании по построенной модели необходимо быть уверенным в ее точности. Но вначале необходимо убедиться в статистической значимости (статистической существенности зависимости) эмпирических данных. Если эмпирические данные значимы, то построенная по ним модель будет точна и соответственно точными будут и полученные по ней прогнозы. В качестве критерия проверки гипотезы о статистической существенности зависимости эмпирических данных рассмотрим критерий Стьюдента.
t
|
y
|
α
|
m=1
|
|
m=2
|
|
m=3
|
|
|
|
|
f(t1)
|
|
f(t2)
|
|
f(t3)
|
|
1
|
1000
|
0
|
31,85
|
0,96815
|
14,02
|
492,99
|
18,4
|
0,9816
|
2
|
850
|
0,5236
|
16,65099
|
0,980411
|
-2,01545
|
426,0077
|
-9,18545
|
1,010806
|
3
|
930
|
1,0472
|
6,63654
|
0,992864
|
5,800093
|
462,1
|
1,420093
|
0,998473
|
4
|
980
|
1,5708
|
4,49
|
0,995418
|
22,32
|
478,84
|
29,49
|
0,969908
|
5
|
970
|
2,0944
|
10,78654
|
0,98888
|
29,45299
|
470,2735
|
33,83299
|
0,965121
|
6
|
953
|
2,61799
|
23,83901
|
0,974985
|
24,67545
|
464,1623
|
17,50545
|
0,981631
|
7
|
940
|
3,14159
|
40,15
|
0,957287
|
22,32
|
458,84
|
17,94
|
0,980915
|
8
|
948
|
3,66519
|
55,34901
|
0,941615
|
36,68256
|
455,6587
|
43,85256
|
0,953742
|
9
|
997
|
4,18879
|
65,36346
|
0,93444
|
64,52701
|
466,2365
|
68,90701
|
0,930886
|
10
|
1000
|
4,71239
|
67,51
|
0,93249
|
85,34
|
457,33
|
78,17
|
0,92183
|
11
|
1320
|
5,23599
|
61,21346
|
0,953626
|
79,87991
|
620,06
|
75,49991
|
0,942803
|
12
|
1450
|
5,75959
|
48,16099
|
0,966786
|
48,99744
|
700,5013
|
56,16744
|
0,961264
|
78
|
12338
|
|
432
|
11,58695
|
432
|
5953
|
432
|
11,59898
|
Итак, имеем:
m=1 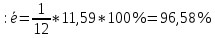
m=2 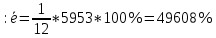
m=3 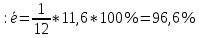
Сравниваем показатели средних ошибок аппроксимации:

Таким образом, наилучшей моделью признается модель m=1.
 |
 Скачать 97.82 Kb.
Скачать 97.82 Kb.