макроекономическое планирование. Макроэкономическое планирование и прогнозирования. Работа некоторого предприятия в 2014 году характеризовалась
 Скачать 97.82 Kb. Скачать 97.82 Kb.
|
|
Задача 4. По данным таблицы необходимо: 1) для каждого показателя у найти индексы сезонности; 2) с помощью индекса сезонности и функции тренда, найденной в задаче 3, получить модель неслучайной составляющей f(x). 3) оценить точность и адекватность полученной модели (доверительная вероятность равна 0,95 и 0,99); 4) на одном чертеже изобразить эмпирические данные, функцию тренда и модель неслучайной составляющей, сделать выводы. Решение: Для того что бы построить модель неслучайной составляющей, найдем индексы сезонности: Средний уровень ряда динамики  = 1028,167 чел. = 1028,167 чел. Подсчитаем индекс сезонности по каждому из месяцев:
Видим, что максимальное число занятых на производстве людей превышает средний уровень в ноябре, декабре. Максимальный рост числа занятых на производстве человек наблюдается в декабре. 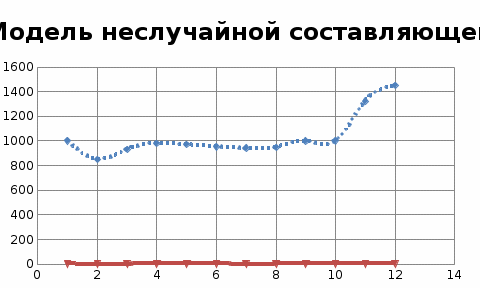 Подсчет индекса сезонности по одному году является ненадежным, так как в этом случае велика вероятность влияния случайных факторов. Задача 5. По данным таблицы необходимо: 1) построить модель неслучайной составляющей f(x) в виде уравнения Фурье (число гармоник взять равным1, 2 и 3); 2) определить, какая из полученных моделей наиболее адекватно и точно описывает эмпирические данные. Доверительная вероятность γ равна 0,95 и 0,99; 3) результаты представить графически. Решение: Модель неслучайной составляющей в виде уравнения Фурье: Для определения коэффициентов составим расчетные таблицы: При м =1 уравнение Фурье имеет вид: 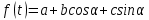
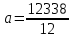  
Запишем уравнение:  При м=2: 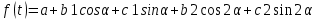
|
