Планирование. Работа некоторого предприятия в 2014 году характеризовалась
 Скачать 97.05 Kb. Скачать 97.05 Kb.
|
|
Задача 6. Используя результаты задач 4 и 5, необходимо: выбрать модель f(x) с помощью которой может быть осуществлен наиболее точный прогноз; по ней произвести точечный прогноз y на: а)январь, б)февраль, в) март2015года. Решение: Исходя из результатов полученных в задаче 4,5, выбираем модель з числом гармоник m=1, по ней можно осуществить наиболее точный прогноз. Для января : s=1, t=13 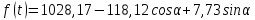 y = 33,83t +808,26
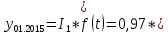 72,16*13) = 910 чел. 72,16*13) = 910 чел.Теперь произведем прогноз с помощью уравнения Фурье: 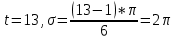 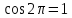 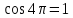 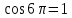 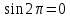 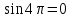 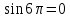 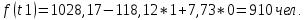 Модель адекватна, поскольку двумя методами подтверждается. Для февраля : s=2, t=14 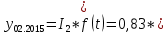 72,16*14) = 838 чел. 72,16*14) = 838 чел.Для марта : s=3, t=15 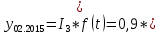 72,16*15) = 974 чел. 72,16*15) = 974 чел.Задача 7. Для ряда значений у из таблицы проверить гипотезы: об отсутствии автокорреляции. Решение: Построим ряд остатков:
Получаем: 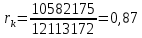 Отсюда: 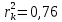 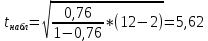 Критическое значения t- критерия находим из таблицы Стьюдента: t(0:0,5:10)=2,23 Поскольку неравенство выполняется : 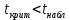 , то гипотеза принимается. , то гипотеза принимается.Таблица 2
Задача 8. По данным таблицы 2 необходимо: вычислить множественный коэффициент корреляции и сделать выводы о характере и тесноте связи между факторными и результативным признаками; Решение: Найдем частные коэффициенты корреляции:
Итак, парные коэффициенты корреляции: 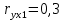 , между показателями х1 и y умеренная связь , между показателями х1 и y умеренная связь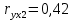 , между показателями х2 и y умереная связь , между показателями х2 и y умереная связь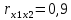 , между показателями х2 и х1 тесная связь , между показателями х2 и х1 тесная связьВычислим множественный коэффициент корреляции: 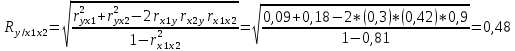 Поскольку, 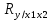 =0,48 стримиться к 0,5, можно сделать вывод о достаточно тесной связи и достаточно хорошей степени линейности корреляционной зависимости. =0,48 стримиться к 0,5, можно сделать вывод о достаточно тесной связи и достаточно хорошей степени линейности корреляционной зависимости. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
