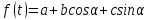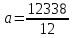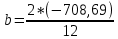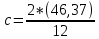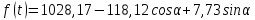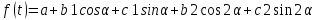Задача 4. По данным таблицы необходимо:
с помощью индекса сезонности и функции тренда, найденной в задаче3, получить модель неслучайной составляющей f(x).
Решение:
Для того что бы построить модель неслучайной составляющей, найдем индексы сезонности:
Средний уровень ряда динамики 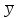 = 1028,167 чел. = 1028,167 чел.
Подсчитаем индекс сезонности по каждому из месяцев:
t
|
y
|
I
|
1
|
1000
|
0,972605
|
2
|
850
|
0,826714
|
3
|
930
|
0,904523
|
4
|
980
|
0,953153
|
5
|
970
|
0,943427
|
6
|
953
|
0,926893
|
7
|
940
|
0,914249
|
8
|
948
|
0,92203
|
9
|
997
|
0,969687
|
10
|
1000
|
0,972605
|
11
|
1320
|
1,283839
|
12
|
1450
|
1,410277
|
Видим, что максимальное число занятых на производстве людей превышает средний уровень в ноябре, декабре.
Максимальный рост числа занятых на производстве человек наблюдается в декабре.
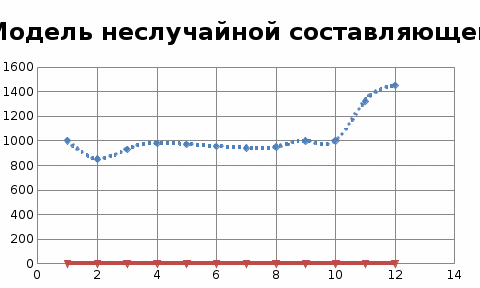
Подсчет индекса сезонности по одному году является ненадежным, так как в этом случае велика вероятность влияния случайных факторов.
Задача 5. По данным таблицы необходимо:
построить модель неслучайной составляющей f(x) в виде уравнения Фурье (число гармоник взять равным1, 2 и3);
определить, какая из полученных моделей наиболее адекватно и точно описывает эмпирические данные. Доверительная вероятность γ равна 0,95 и 0,99;
Решение:
Модель неслучайной составляющей в виде уравнения Фурье:
Для определения коэффициентов составим расчетные таблицы:
При м =1 уравнение Фурье имеет вид:
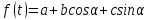
t
|
y
|
|
cosa
|
sina
|
ycosa
|
ysina
|
1
|
1000
|
0
|
1
|
0
|
1000
|
0
|
2
|
850
|
0,5236
|
0,866025
|
0,5
|
736,1216
|
425
|
3
|
930
|
1,0472
|
0,5
|
0,866025
|
465
|
805,4036
|
4
|
980
|
1,5708
|
6,13E-17
|
1
|
6E-14
|
980
|
5
|
970
|
2,0944
|
-0,5
|
0,866025
|
-485
|
840,0446
|
6
|
953
|
2,61799
|
-0,86603
|
0,5
|
-825,322
|
476,5
|
7
|
940
|
3,14159
|
-1
|
1,23E-16
|
-940
|
1,15E-13
|
8
|
948
|
3,66519
|
-0,86603
|
-0,5
|
-820,992
|
-474
|
9
|
997
|
4,18879
|
-0,5
|
-0,86603
|
-498,5
|
-863,427
|
10
|
1000
|
4,71239
|
-1,8E-16
|
-1
|
-1,8E-13
|
-1000
|
11
|
1320
|
5,23599
|
0,5
|
-0,86603
|
660
|
-1143,15
|
12
|
1450
|
5,75959
|
0,866025
|
-0,5
|
1255,737
|
-725
|
Сумма
|
12338
|
|
-0,86603
|
0,5
|
-708,693
|
46,36741
|
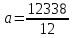
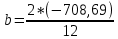
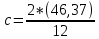
a
|
1028,167
|
b
|
-118,115
|
c
|
7,727901
|
Запишем уравнение:
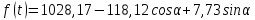
При м=2:
t
|
y
|
α
|
2α
|
cos2α
|
sin2α
|
y*cos2α
|
y*sin2α
|
1
|
1000
|
0
|
0
|
1
|
0
|
1000
|
0
|
2
|
850
|
0,523599
|
1,047198
|
0,5
|
0,866025
|
425
|
736,1216
|
3
|
930
|
1,047198
|
2,094395
|
-0,5
|
0,866025
|
-465
|
805,4036
|
4
|
980
|
1,570796
|
3,141593
|
-1
|
1,23E-16
|
-980
|
1,2E-13
|
5
|
970
|
2,094395
|
4,18879
|
-0,5
|
-0,86603
|
-485
|
-840,045
|
6
|
953
|
2,617994
|
5,235988
|
0,5
|
-0,86603
|
476,5
|
-825,322
|
7
|
940
|
3,141593
|
6,283185
|
1
|
-2,5E-16
|
940
|
-2,3E-13
|
8
|
948
|
3,665191
|
7,330383
|
0,5
|
0,866025
|
474
|
820,9921
|
9
|
997
|
4,18879
|
8,37758
|
-0,5
|
0,866025
|
-498,5
|
863,4273
|
10
|
1000
|
4,712389
|
9,424778
|
-1
|
3,68E-16
|
-1000
|
3,68E-13
|
11
|
1320
|
5,235988
|
10,47198
|
-0,5
|
-0,86603
|
-660
|
-1143,15
|
12
|
1450
|
5,759587
|
11,51917
|
0,5
|
-0,86603
|
725
|
-1255,74
|
сумма
|
12338
|
|
|
6,11E-16
|
0
|
-48
|
-838,313
|
|
 Скачать 97.05 Kb.
Скачать 97.05 Kb.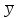 = 1028,167 чел.
= 1028,167 чел.