Планирование. Работа некоторого предприятия в 2014 году характеризовалась

• Название: Работа некоторого предприятия в 2014 году характеризовалась
• Анкор: Планирование
• Дата: 21.07.2021
• Размер: 97.05 Kb.
• Имя файла: yana planirovanie.docx
• Тип: Документы; #224962
• страница: 1 из 5

Работа некоторого предприятия в 2014 году характеризовалась данными, приведенными в таблице1.

Таблица 1

Число занятых на производстве (на конец месяца),чел.

№	Месяц	Показатели деятельности предприятия
1	Январь	1000
2	Февраль	850
3	Март	930
4	Апрель	980
5	Май	970
6	Июнь	953
7	Июль	940
8	Август	948
9	Сентябрь	997
10	Октябрь	1000
11	Ноябрь	1320
12	Декабрь	1450

Задача 1. Для ряда динамики из таблицы необходимо: произвести анализ уровней ряда динамики цепным и базисным способами (за базисный принять уровень января 2014г.);

Показатели динамики числа занятых на производстве человек за 2014 год, представлены в таблице 2.

Таблица 2

№	Месяц	Число уволенных человек	Абсолютные приросты		Темпы роста		Темпы прироста
			Цепные	Базисные	Цепне	Базисные	Цепные	Базисные
1	Январь	1000	-	-	100%	100%	-	-
2	Февраль	850	-150	-150	85%	85%	-15%	-15%
3	Март	930	80	-70	109,41%	93%	9,41%	-7%
4	Апрель	980	50	-20	105,38%	98%	5,38%	-2%
5	Май	970	-10	-30	98,98%	97%	-1,02%	-3%
6	Июнь	953	-17	-47	98,23%	95,3%	-1,77%	-4,7%
7	Июль	940	-13	-60	98,64%	94%	-1,36%	-6%
8	Август	948	8	-52	100,85%	94,8%	0,85%	-5,2%
9	Сентябрь	997	49	-3	105,17%	99,7%	5,17%	-0,3%
10	Октябрь	1000	3	0	100,3%	100%	0,3%	0%
11	Ноябрь	1320	320	320	132%	132%	32%	32%
12	Декабрь	1450	130	450	109,85%	145%	9,85%	45%

Абсолютные приросты цепные: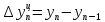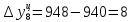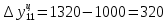























Абсолютные приросты базисные: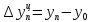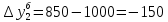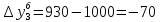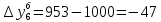























Аналогично, находим другие показатели, занося в таблицу.

Темпы роста цепные:

Темпы роста базисные:

Темпы прироста цепные:



Темпы прироста базисные:



Задача 2. Для ряда динамики из таблицы выяснить факт наличия или отсутствия неслучайной составляющей. Проверку провести тремя способами: используя критерий «восходящих» и «нисходящих»серий.

1. 
   Проверим факт наличия или отсутствия неслучайной составляющей с помощью критерия «восходящих» и «нисходящих» серий.
   

Заменяем значения уровней последовательностью знаков + или — соглас­но следующему правилу: на i'-м месте ставим знак:
+, если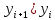
-, если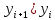

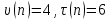t	y
1	1000	-
2	850	-
3	930		+
4	980		+
5	970		-
6	953		-
7	940		-
8	948		+
9	997		+
10	1000		+
11	1320		+
12	1450		+

Проверим условие: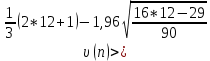


4>5, не выполняется.
Это означает, что с вероятностью 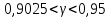, можно утверждать, что в данном раде динамики, есть неслучайная составляющая.

Задача 3. Для ряда динамики из таблицы построить функцию тренда в предположении линейной, показательной и параболической зависимостей.

t	t^2	t^3	t^4	y	ln(y)	t*y	t^2*y	t*ln(y)
1	1	1	1	1000	6,907755	1000	1000	6,907755
2	4	8	16	850	6,745236	1700	3400	13,49047
3	9	27	81	930	6,835185	2790	8370	20,50555
4	16	64	256	980	6,887553	3920	15680	27,55021
5	25	125	625	970	6,877296	4850	24250	34,38648
6	36	216	1296	953	6,859615	5718	34308	41,15769
7	49	343	2401	940	6,84588	6580	46060	47,92116
8	64	512	4096	948	6,854355	7584	60672	54,83484
9	81	729	6561	997	6,904751	8973	80757	62,14276
10	100	1000	10000	1000	6,907755	10000	100000	69,07755
11	121	1331	14641	1320	7,185387	14520	159720	79,03926
12	144	1728	20736	1450	7,279319	17400	208800	87,35183
78	650	6084	60710	12338	83,09009	85035	743017	544,3655

Подставляем найденные значения в системы нормальных уравнений:

1. 
   Линейная модель:
   

y = 33,83t +808,26

2. 
   Параболическая модель:
   

y = 8,85t² – 81,24t + 1076

3. 
   Показательная модель: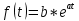
   

y = 836,8e^0,029t