теодолитный ход инструкция. 4. Теодолитный ход. Инструкция (1). Работа Вычисление координат вершин теодолитного хода Общие сведения
 Скачать 84.09 Kb. Скачать 84.09 Kb.
|
Работа 4. Вычисление координат вершин теодолитного хода4.1. Общие сведенияПри создании съёмочного обоснования, обеспечивающего выполнение топографических съёмок, часто используются теодолитные ходы. Они представляют собой системы ломаных линий, образующих замкнутые или разомкнутые полигоны. В вершинах полигонов измеряют углы одним полным приёмом теодолитами технической точности, например 2Т30П или 4Т15П. Кроме того, измеряют расстояния между смежными вершинами. Применяют для этого, в зависимости от периметра полигона, стальные землемерные ленты или дальномеры, обеспечивающие точность измерений от 1:1000 до 1:3000. Длина хода регламентируется масштабом съёмки и точностью измерений. Теодолитные ходы, как правило, прокладывают между опорными пунктами ранее созданных геодезических сетей. Каждый студент получает задание, в котором даны: схема теодолитного хода, его привязки к исходным пунктам и направлениям, координаты исходных пунктов, значения примычных углов, измеренные углы на вершинах теодолитного хода и горизонтальные расстояния между смежными вершинами. Конечный результат работы – координаты вершин хода и план, на который ход нанесён. Выполняют работу в следующей последовательности: - по координатам исходных пунктов решают обратные геодезические задачи с целью определения дирекционных углов исходных сторон, - уравнивают примычные углы и вычисляют дирекционный угол первой стороны теодолитного хода, - определяют угловую невязку теодолитного хода, и, если она не превышает допуска, распределяют поровну в измеренные углы, - по исправленным углам вычисляют дирекционные углы всех сторон теодолитного хода, - определяют приращения координат, линейные и относительную невязки хода. Если последняя в допуске, то невязки по осям координат распределяют в приращения координат пропорционально длинам сторон, получают исправленные приращения, - вычисляют координаты всех вершин хода, - составляют план теодолитного хода. 4.2. Обработка теодолитного хода4.2.1. Вычисление дирекционных углов исходных направленийДля вычисления дирекционных углов исходных направлений необходимо решать обратные геодезические задачи. Решение одной из них приведено в табл.7. Таблица 7 Вычисление обратной геодезической задачи
Формулы для вычислений
4.2.2. Уравнивание углов на исходном пунктеЕ  сли на исходном пункте в теодолитный ход включены два исходных направления (например, 1-В и 1-Cнарис.7), то разность их дирекционных углов обычно не равна разности измеренных примычных углов. Расхождение между указанными разностями не должно превышать 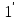 . Для последующих вычислений примычные углы надо уравнять и вычислить дирекционный угол стороны хода. . Для последующих вычислений примычные углы надо уравнять и вычислить дирекционный угол стороны хода.На рис.7 приведён пример уравнивания углов на пункте 1. Оно выполнено следующим образом. На схему выписаны измеренные примычные углы(βB-2, βC-2)и вычисленные дирекционные углы(α1-B, α1-C) По разности примычных углов контрольный угол равен 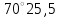 ′. по разности дирекционных углов его значение ′. по разности дирекционных углов его значение  Значит – 0.4 - это невязка. Её надо распределить. Для этого угол βC-2 уменьшен на 0,2´, а угол βB-2 на столько же увеличен. Исправленные углы выписаны на ту же схему и подчёркнуты. Значит – 0.4 - это невязка. Её надо распределить. Для этого угол βC-2 уменьшен на 0,2´, а угол βB-2 на столько же увеличен. Исправленные углы выписаны на ту же схему и подчёркнуты.4.2.3. Уравнивание горизонтальных углов теодолитного ходаД  альнейшую обработку материалов наблюдений рассмотрим на примере замкнутого теодолитного хода (рис.8). Вычисления выполняют в ведомости (табл.8). Вначале из полевого журнала выписывают номера вершин теодолитного хода, средние значения горизонтальных углов и горизонтальные проложения длин сторон хода (в гр.1,2и5). Подсчитывают сумму измеренных горизонтальных углов Σbизм (в данном случае они левые по ходу). Ее сравнивают с теоретической суммой, которая для внутренних углов замкнутого полигона, содержащего n углов, равна:
Разность между суммой измеренных углов и теоретической суммой даст значение угловой невязки 
Ее сравнивают с допустимой угловой невязкой хода, которую вычисляют по формуле:
Если ƒß ≤ ƒβ пред., то полученную невязку распределяют поровну во все измеренные углы с точностью до 0,1′ со знаком обратным невязке. Если невязка не делится без остатка на число углов хода, то большие поправки вводят в углы с более короткими сторонами. Контроль: сумма поправок должна быть равна невязке с обратным знаком. Правильность уравнивания углов контролируют также подсчётом суммы углов, исправленных поправками. Она должна равняться теоретической. 4.2.4. Вычисление дирекционных угловВначале вычисляют дирекционный угол первой стороны теодолитного хода. Для этого используют дирекционный угол одной из исходных сторон и один из уравненных примычных углов. В частности, из рис.7 видно, что для этого можно воспользоваться следующими соотношениями: 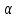 1-2 = 1-2 = 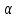 1-B +B-2, 1-B +B-2, 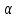 1- 2 = 1- 2 = 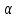 1-C +C-2 1-C +C-2Вычисление дирекционных углов последующих сторон теодолитного хода выполняют по формулам:
Если один из дирекционных углов получился больше 360°, то его нужно уменьшить на эту величину; если сумма углов меньше вычитаемого, то её следует увеличить на 360°. В теодолитном ходе контролем вычисления дирекционных углов его сторон является получение дирекционного угла первой стороны (в замкнутом ходе) или конечной стороны (в разомкнутом ходе). 4.2.5. Вычисление приращений координат точек теодолитного ходаПриращения прямоугольных координат вычисляют по формулам:
где S – горизонтальное проложение стороны теодолитного хода; 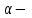 её дирекционный угол. её дирекционный угол. Вычисления ведут с точность до 0,01 м. Знаки приращений соответствуют знакам тригонометрических функций 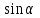 и и  , и в геодезии указываются обязательно. Заданием предусмотрено вычислять приращения прямоугольных координат с помощью микрокалькулятора, поэтому необходимо обратить внимание на режим его работы. Для работы с тригонометрическими функциями в градусной мере на дисплее должна высвечиваться надпись DEG, У вводимого угла десятые минут следует переводить в секунды. , и в геодезии указываются обязательно. Заданием предусмотрено вычислять приращения прямоугольных координат с помощью микрокалькулятора, поэтому необходимо обратить внимание на режим его работы. Для работы с тригонометрическими функциями в градусной мере на дисплее должна высвечиваться надпись DEG, У вводимого угла десятые минут следует переводить в секунды.Вычисленные приращения координат записывают в ведомость. Затем их алгебраически суммируют, отдельно 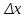 и и 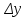 . Для замкнутого хода они являются невязками . Для замкнутого хода они являются невязками 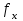 и и 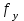 соответственно по осям координат X и Y, т.е.: соответственно по осям координат X и Y, т.е.: 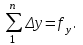 Качество измерений углов и длин сторон теодолитного хода оценивают по относительной ошибке хода. Для этого вначале вычисляют его абсолютную ошибку: 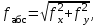 и от неё переходят к относительной ошибке:  где Р – периметр полигона, м. Относительная ошибка не должна превышать 1/2 000 периметра. Если допуск выполняется, то в приращения координат вводят поправки  и и 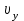 пропорционально длинам сторон: пропорционально длинам сторон: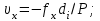 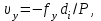 где d – длина стороны хода, м. Таблица 8
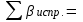 54000,0 ƒx =−0,08 м ƒy =−0,22 м 54000,0 ƒx =−0,08 м ƒy =−0,22 м 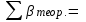 54000,0 54000,0 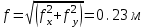 ƒβ = +2,1 ; ƒβ пред.= ±2,2 ; ƒβ≤ ƒβ пред ; ƒотн.=   Полученные поправки округляют до сотых долей метра и подписывают их над соответствующими приращениями. Контроль: сумма поправок должна быть равна невязке с обратным знаком. Затем вычисляют исправленные приращения, сумма которых по каждой оси должна быть равна нулю:   По исправленным приращениям определяют координаты вершин теодолитного хода: 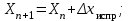  Контроль - получение координат исходного пункта, от которого и начинали вычисления. 4.2.6. Разбивка основы и нанесение точек теодолитного ходаРазбивку координатной сетки производят твердым карандашом на листе чертёжной бумаги формата А4 при помощи циркуля-измерителя и масштабной линейки, действуя при этом следующим образом. Между углами листа выверенной линейкой проводят диагонали. От точки их пересечения по всем четырём направлениям откладывают равные отрезки, концы которых соединяют прямыми линиями. Получают прямоугольник, являющийся базой для построения сетки. На сторонах прямоугольника циркулем-измерителем откладывают отрезки по 10 см вверх и вправо от его нижнего левого угла. Соединив соответствующие точки прямыми линиями, получают сетку квадратов. При необходимости, используя измеритель и линейку, сетку перемещают параллельно самой себе. Правильность построения проверяют сравнением длин сторон квадратов с номиналом (10 см) и их диагоналей между собой; расхождения не должны превышать 0,2 мм. Затем сетку оцифровывают. Подписи сторон сетки должны быть кратными длине отрезка местности, которому на плане соответствует сторона квадрата (10 см), и такими, чтобы все точки теодолитного хода находились в пределах основы. Для этого используют ранее вычисленные значения минимальных и максимальных координат. Для нанесения точки хода на план по её координатам, прежде всего, определяют квадрат сетки, которому она принадлежит. От нижней стороны этого квадрата на двух его вертикальных сторонах с учётом масштаба откладывают отрезки, равные разности абсцисс точки хода и нижней стороны квадрата. Точки накалывают иголкой циркуля-измерителя и соединяют по линейке тонкой прямой линией. Затем от левой стороны квадрата по двум горизонтальным сторонам откладывают ординату. Пересечение линий и дает положение точки хода на плане. Её накалывают, обводят квадратиком со стороной 2 мм, если точка исходная, или кружком диаметром 2 мм, если это вершина хода и подписывают. Все построения выполняют с точностью 0,2 мм. Контроль качества нанесения точек теодолитного хода на план производят по расстояниям между ними или по координатам, которые измеряют с помощью масштабной линейки. Разность расстояний, полученных на плане и взятых из ведомости, не должна превышать (0,4 мм) М. Смежные точки соединяют отрезками, толщиной 0,3 мм, кроме того, с помощью транспортира на план наносят исходные стороны и показывают примычные углы. В нижней части плана указывают его масштаб 1:M, а в верхней -принадлежность работы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


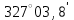
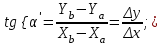
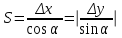

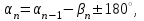 - для правых углов,
- для правых углов, - для левых углов
- для левых углов