РТЦиС_метода к лабам. Радиотехнические цепи и сигналы лабораторный практикум
 Скачать 1.84 Mb.
|
Содержание отчетаОтчет по работе должен включать в себя следующие материалы:
1) трехзвенная RС-цепь с R1 = 1,5 кОм, C1 = 0,01 мкФ; 2) четырехзвенная RС-цепь с R2 = 1,5 кОм, C2 = 0,01 мкФ; 3а) мост Вина с R3 = 1 кОм, C3 = 3 мкФ; 3б) мост Вина с R3 = 1,2 кОм, С3 = 3 мкФ;
Контрольные вопросы
12. ИССЛЕДОВАНИЕ ПРОЦЕССА САМОВОЗБУЖДЕНИЯ LC АВТОГЕНЕРАТОРАЦель работы — изучение необходимых и достаточных условий самовозбуждения автогенераторов с узкополосными цепями обратной связи и собственно процесса самовозбуждения. 12.1. Теоретические сведенияВ радиотехнике генератором называют устройство, преобразующее энергию источника питания (чаше всего источника постоянного тока) в энергию электрических колебаний. Колебания могут быть как периодические, так и непериодические. Последние представляют собой случайный электрический процесс, называемый шумовым сигналом. Периодические колебания могут быть как гармоническими (в форме синусоиды), так и в виде последовательности сигналов другой формы (прямоугольной, треугольной, пилообразной и т. д.). Форма колебаний определяется частотными характеристиками цепи обратной связи. В данной работе исследуется генератор, цепь обратной связи которого реализуется в виде последовательной LC цепи, входящей в параллельный колебательный контур. Из теории цепей с обратной связью (ЦОС) известно, что коэффициент передачи ЦОС  , где  — коэффициент передачи четырехполюсника, который должен быть охвачен обратной связью; (i) — коэффициент передачи четырехполюсника обратной связи. Оба эти коэффициента передачи удобно представить в комплексной форме, через модуль и фазу:  ,  , где — сдвиг фаз в четырехполюснике К, — сдвиг фаз в четырехполюснике . Тогда  . Если  (n = 0, 1, 2, 3, …), то реализуется положительная обратная связь, если  (n = 0, 1, 2, 3, …), то реализуется отрицательная обратная связь. Обычно в качестве четырехполюсника K используется биполярный или полевой транзистор. При включении его по схеме с общим эмиттером или общим истоком получается инвертирующий усилитель, вносящий фазовый сдвиг = . Следовательно, для получения положительной обратной связи фаза также должна быть равна . При положительной обратной связи  всегда больше, чем  . При приближении произведения  к единице  стремится к бесконечности. При этом бесконечно малые напряжения на входе транзистора вызывают конечные напряжения на выходе, т. е. схема работает как генератор. Далее будет показано, что при выполнении этого условия генератор будет генерировать колебания с постоянной амплитудой. Поэтому данное условие называется балансом амплитуд. Условие, обеспечивающее положительную обратную связь (), называется балансом фаз. Для более детального анализа процессов в автогенераторе (АГ) рассмотрим схему емкостной трехточки (схема Колпитца), которая используется в лабораторном макете. На рис. 12.1 приведена эта схема с учетом только цепей высокой частоты (цепи питания исключены). Рис. 12.1 Элементы L1, C1 и C2 образуют параллельный колебательный контур, R1 —нагрузочный резистор, в сопротивление которого включены сопротивления потерь элементов контура и потери, вносимые базовой и коллекторной цепями транзистора. На резонансной частоте  справедливо следующее уравнение для реактивных сопротивлений элементов контура:  .Пусть напряжение на контуре (на конденсаторе С2) равно  , а напряжение между базой и эмиттером равно  (это напряжение является напряжением обратной связи). Четырехполюсник обратной связи образован катушкой индуктивности L1 и конденсатором С1. Его коэффициент передачи  , но из предыдущего уравнения  и коэффициент передачи (коэффициент обратной связи)  . Знак «минус» означает, что фаза напряжения повернута на 180 по отношению к фазе напряжения . Знак «минус» будет сохраняться до тех пор, пока  больше, чем  , т. е. пока цепочка L1, C1 имеет индуктивную реакцию. Меняя , можно менять условия самовозбуждения АГ (изменяя значение знаменателя в выражении для  ). Напряжение между коллектором и эмиттером определяется крутизной ВАХ транзистора  , где  — коллекторный ток транзистора:  . Крутизна S не является постоянной величиной; она зависит от постоянной составляющей напряжения . Для дальнейшего анализа заменим схему (рис. 12.1) на эквивалентную (рис. 12.2). Вместо транзистора включим источник тока, имитирующий переменную составляющую коллекторного тока  . ВАХ транзистора (как биполярного, так и полевого) мало зависят от напряжения на коллекторе (стоке), поэтому ток коллектора определяется в основном напряжением . Цепочку L1, C1 заменим эквивалентной индуктивностью L, конденсатор С2 — конденсатором С, резистор R1 — резистором R. 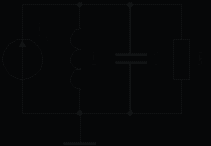Рис. 12.2 Ток источника создает в ветвях схемы токи  ,  ,  . Очевидно, что справедливо уравнение .Учитывая, что  ,  ,  ,  , продифференцируем уравнение для токов по времени и получим дифференциальное уравнение второго порядка относительно следующего вида (далее индекс «кэ» опущен):  . Это уравнение является приближенным, так как крутизна — нелинейная функция U и, следовательно, зависит от времени. Однако пока будем считать ее постоянной. Принимая во внимание, что  ( — резонансная частота контура АГ), перепишем уравнение в следующем виде: . Решение этого уравнения (с учетом того, что  ):  . Видно, что рост напряжения на контуре возможен, только если произведение  больше единицы. В начале процесса, пока амплитуда напряжения на контуре заметно меньше напряжения питания коллекторной цепи, крутизна остается практически постоянной. При дальнейшем росте амплитуды, ввиду нелинейности ВАХ транзистора, крутизна начинает уменьшаться и процесс роста заканчивается установлением «баланса амплитуд», когда выполняется равенство  , после чего амплитуда напряжения на контуре остается постоянной (этот режим называется стационарным, как и значение крутизны, при котором он устанавливается —  ). Очевидно, что значение зависит от и R. Обозначим постоянную времени процесса через , тогда  . Наблюдая на экране осциллографа процесс установления колебаний напряжения на выходе АГ, можно измерить значение . Оно будет различным на разных участках процесса нарастания. Так как значения , R и C постоянны, изменения зависят только от крутизны характеристики транзистора. По измеренным значениям можно найти значения крутизны на разных участках процесса. Необходимо отметить, что измеренная таким образом крутизна будет так называемой крутизной по первой гармонике  , так как транзистор работает с отсечкой коллекторного тока, а резонансный контур АГ имеет высокую добротность и узкую полосу пропускания, фильтруя только первую гармонику коллекторного тока. Тогда  . Для стационарного режима  .Рассмотрим теперь влияние на процесс самовозбуждения дополнительного фазового сдвига, вносимого фазосдвигающей цепью (фазовращатель, линия задержки, отрезок кабеля), включенной между базой транзистора и цепью, соединяющей L1 и С1. Очевидно, что в этом случае фаза напряжения будет больше180 на величину набега фазы, вносимого фазовращателем. Следовательно, теперь условие баланса фаз будет выполняться на другой частоте, на которой сдвиг фаз в точке соединения L1 и С1 будет меньше 180 на величину набега фазы. Так как фазовые характеристики имеют отрицательный наклон, эта частота будет меньше, чем частота в случае отсутствия фазовращателя. На этой частоте (отличной от резонансной) коэффициент передачи транзистора  , где  и  . Очевидно, что на резонансной частоте  и  . Определим условие баланса фаз при наличии фазовращателя, который дает сдвиг фаз, равный  . Коэффициент передачи транзистора (с учетом поворота фазы на 180º)  , и произведение  . Очевидно, что новое условие баланса фаз будет  . Оценим значение частоты, которую будет генерировать АГ при дополнительном фазовом сдвиге. Пусть эта частота  . Полагая, что добротность контура АГ высока, приближенное выражение для новой частоты генерации  . Значение |Z| при сдвиге частоты будет уменьшаться по отношению к R при росте , что потребует увеличения крутизны S для сохранения значения и приведет к замедлению роста амплитуды колебаний. Если же произведение S|Z| станет меньшим единицы, то самовозбуждение будет вообще невозможным. |