РТЦиС_метода к лабам. Радиотехнические цепи и сигналы лабораторный практикум

• Название: Радиотехнические цепи и сигналы лабораторный практикум
• Анкор: РТЦиС_метода к лабам.doc
• Дата: 26.12.2017
• Размер: 1.84 Mb.
• Имя файла: РТЦиС_метода к лабам.doc
• Тип: Практикум; #13019
• страница: 20 из 25

Контрольные вопросы

1. 
   В чем состоят особенности анализа нелинейных цепей?
   
2. 
   Какие основные способы аппроксимации характеристик нелинейных цепей Вам известны?
   
3. 
   Дайте определение угла отсечки, в каких случаях используется это понятие?
   
4. 
   Как влияет нагрузка на ток, протекающий через диод при гармоническом воздействии?
   
5. 
   В чем различие между коэффициентами и функциями Берга? Как необходимо организовать эксперимент, чтобы непосредственно измерить коэффициенты Берга?
   
6. 
   При каких углах отсечки ? Как интерпретировать это обстоятельство?
   
7. 
   Опишите методику экспериментального определения графиков коэффициентов Берга.
   
8. 
   Может ли нелинейный элемент работать в линейном режиме? Если да, то чему равен в этом случае угол отсечки?
   
9. 
   Нелинейный элемент имеет ВАХ с ограничением, и на выходе появляются ограниченные cos-импульсы тока. Рассчитайте амплитуды гармоник выходного тока, используя коэффициенты Берга.
   
10. 
    Изобразите взаимное положение ВАХ нелинейного элемента и входного гармонического сигнала при углах отсечки  = 0, 90, 180.
    
11. 
    ВАХ нелинейного элемента аппроксимирована кусочно-нелинейно: прямой i = 0, u  0 и параболой i = a₂u², u > 0. Найдите амплитуды гармоник . Можно ли при этом воспользоваться коэффициентами Берга?
    
12. 
    На нелинейный элемент с кусочно-линейной ВАХ подано АМ коле­бание. Изобразите выходной ток и его спектр.
    

10. НЕЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ УСТРОЙСТВА

Цель работы — исследование основных нелинейных радиотехнических устройств и функциональных преобразований сигналов в этих устройствах.

10.1. Теоретические сведения

В целом ряде радиотехнических устройств необходимо использовать нелинейные элементы.
Аппроксимация нелинейных характеристик. Для анализа и расчетов схем, содержащих нелинейные элементы, необходимо аналитическое, в виде формулы, представление нелинейной ВАХ. Используются различные способы аппроксимации — замены таблично (иногда и аналитически) заданной характеристики функциями, приближенно отражающими поведение реальной ВАХ нелинейного двухполюсника в представляющем интерес диапазоне изменения аргумента. При выборе вида аппроксимирующих функций учитывают требуемую точность результата, пределы изменения входного воздействия и удобство выбранной функции для аналитических расчетов. Наиболее распространенными видами аппроксимации являются полиномиальная, кусочно-линейная и показательная. Для простейшего качественного анализа работы основных нелинейных радиотехнических устройств удобна полиномиальная аппроксимация. Полиномиальная аппроксимация. Пусть i = f(u) (см. рис. 9.1 ) является графически заданной (экспериментально снятой) ВАХ. Будем искать представление этой характеристики в виде ряда Маклорена
i = f(u) = a₀ + a₁u + a₂u² + a₃u³ + a₄u⁴ + … . (10.1)

Ограничиваясь n членами ряда: i = f(u) = a₀ + a₁u + a₂u² + … + a_n–1u^n–1, запишем, используя график, систему уравнений:

i₁ = f(u₁) = a₀ + a₁u₁ + a₂u₁² + … + a_n–1u₁^n–1,

i₂ = f(u₂) = a₀ + a₁u₂ + a₂u₂² + … + a_n–1u₂^n–1,

i₃ = f(u₃) = a₀ + a₁u₃ + a₂u₃² + … + a_n–1u₃^n–1,

…

i_n = f(u_n) = a₀ + a₁u_n + a₂u_n² + … + a_n–1u_n^n–1.

Решая полученную систему линейных уравнений относительно неизвестных a₀, a₁, a₂, …, a_n–1, получим ВАХ полупроводникового диода, аппроксимированную полиномом n й степени на участке u  [u₁, u_n].

Спектральный состав тока в цепи с нелинейным сопротивлением. Пусть ВАХ нелинейного сопротивления (в качестве которого в лабораторном макете используется полупроводниковый диод) аппроксимирована полиномом третьей степени:

, (10.2)

где  — размерные коэффициенты.

Подадим на полупроводниковый диод постоянное напряжение смещения и сумму двух гармонических колебаний

. (10.3)

Подставив сумму (10.3) в полином (10.2) и производя элементарные тригонометрические преобразования, определим амплитуды гармоник тока:



(10.4)

Спектр тока в цепи богат гармониками. При нелинейности элемента, требующей для аппроксимации полинома более высокой степени, число гармонических составляющих в спектре возрастает. Спектр тока содержит в общем случае гармоники с комбинационными частотами , причем m и n представляют целые числа, максимальные значения которых в сумме не превосходят степени аппроксимирующего полинома. Ещё более сложная картина получается при подаче на нелинейную цепь радиосигналов, имеющих богатый спектральный состав.

Эти эффекты используются для осуществления амплитудной модуляции, гетеродинирования и детектирования.

Амплитудная модуляцияосуществляется изменением амплитуды несущего (с частотой ) гармонического колебания по закону модулирующего сигнала. Однотональное амплитудно-модулированное (АМ) колебание записывают как

, (10.5)

где  — коэффициент модуляции, U — амплитуда колебаний несущей частоты,  — амплитуда низкочастотного колебания с частотой .

Переписав выражение (10.5) в виде

, (10.6)

получаем представление однотонального АМ-колебания в виде суммы трех гармоник: несущей с частотой , верхней и нижней боковых с частотами и соответственно.

Схема устройства для формирования АМ-колебаний с помощью нелинейной цепи представлена на рис. 10.1.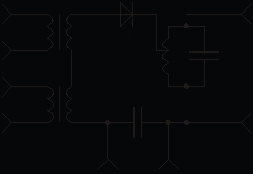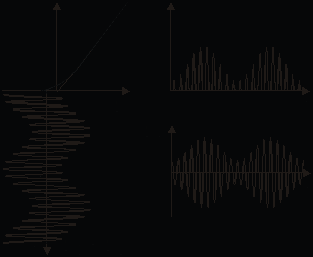



Рис. 10.1 Рис. 10.2

Рассмотрим случай модуляции амплитуды гармонического колебания колебанием (рис. 10.2). Пусть ВАХ нелинейного элемента (диод VD на рис. 10.1) представлена полиномом вида (10.1), тогда, учитывая результаты (10.3) и вводя обозначения и , выделим спектральные составляющие с частотами , , сумма которых в соответствии с (10.6) и представляет тональное АМ-колебание. Выделяя из спектра тока в цепи эти составляющие с помощью нагрузки — параллельного колебательного контура, настроенного на частоту и имеющего полосу запирания не меньше, чем 2, получим напряжение с амплитудной модуляцией. Коэффициент модуляции

. (10.7)

Из выражения (10.7) следует, что огибающая полученного АМ-колебания не воспроизводит закон модуляции, так как m зависит от нелинейно. Но при квадратичной () ВАХ коэффициент модуляции

. (10.8)

В этом случае закон модуляции воспроизводится без искажений.

На рис. 10.2 представлены временные диаграммы работы амплитудного модулятора.

Гетеродинированиесостоит в переносе спектра сигнала по частоте без изменения структуры спектра. Гетеродинирование также осуществляется с использованием нелинейного элемента и может быть реализовано с помощью схемы, показанной на рис. 10.1.

Пусть u(t) — сигнал, подлежащий гетеродинированию, а  — средняя частота его спектра;  — колебание, создаваемое вспомогательным генератором (гетеродином). Тогда параллельный колебательный контур (нагрузка) должен быть настроен на частоту и иметь полосу запирания, равную ширине спектра сигнала . Для получения минимального числа нежелательных продуктов преобразования характеристика нелинейного элемента должна быть близка к квадратичной, тогда спектр выходного сигнала будет содержать только составляющие , , , которые легко отфильтровать. Нелинейных искажений перенесенного на частоту сигнала при этом нет.

Амплитудное детектирование заключается в выделении из радиосигнала его огибающей, связанной с модулирующим сигналом. Рассмотрим преобразование однотонального АМ-колебания нелинейным двухполюсником с квадратичной ВАХ:

. (10.9)

Подставив в (10.9) выражение входного высокочастотного напряжения :



,

выделим постоянную составляющую тока и, вычитая из нее ток покоя , найдем характеристику детектирования квадратичного детектора:

. (10.10)

Характеристика детектирования (10.10)оказывается параболической. При таком детектировании возникают заметные искажения: при тональной АМ ток в цепи

,

помимо постоянной составляющей, от которой легко избавиться с помощью, например, разделительного конденсатора, содержит гармонику с частотой  и создающее искажения колебание на частоте 2. Если же модуляция осуществляется сложным (содержащим много гармоник) сигналом, то, кроме гармоник на частотах 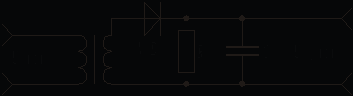, возникают и комбинационные колебания, приводящие к дополнительным искажениям полезного сигнала.




Рис. 10.3
Принципиальная схема устройства, с помощью которого осуществляют детектирование АМ-сигналов, приведена на рис. 10.3. Отличие этой схемы амплитудного диодного линейного детектора от схемы модулятора состоит в том, что здесь на входе действует одно сложное входное колебание, а в качестве фильтрующего элемента (нагрузки) используется фильтр нижних частот (RC-цепочка). Эта схема используется при достаточно больших уровнях АМ-колебания, при этом реализуется режим детектирования, называемый линейным. В этом случае ВАХ нелинейного элемента можно аппроксимировать кусочно-ломаной зависимостью (см. 9.1 настоящего пособия), а амплитуду выходного напряжения считать пропорциональной амплитуде модулирующего напряжения. В этом смысле и говорят о линейности процедуры детектирования, которая является принципиально нелинейной операцией.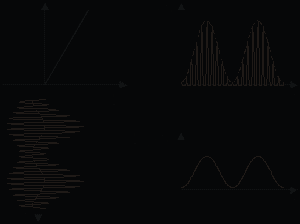




Рис. 10.4
При более строгом анализе детектирования существенным оказывается учет реакции нагрузки, т. е. падения напряжения частоты  на RC-фильтре: . К диоду приложена сумма напряжений . На рис. 10.4 приведены соответствующие временные диаграммы.

Со спектральной точки зрения все три рассмотренных процесса — модуляция, детектирование и гетеродинирование — являются частными случаями преобразования спектра, сводящегося к его переносу по оси частот. При амплитудной модуляции спектр модулирующего сигнала (обычно низкочастотный) переносится в область высоких частот. При детектировании спектр модулированного радиосигнала переносится в область нулевой частоты. Гетеродинирование — промежуточный случай (спектр радиосигнала сдвигается в заданную область по оси частот).