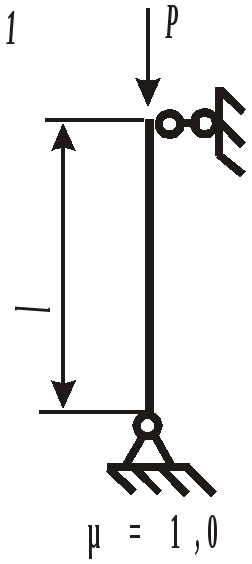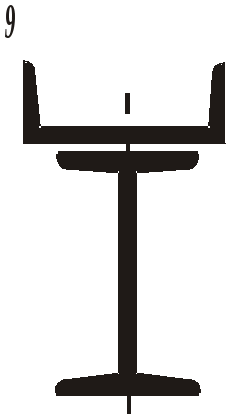Техническая механика. Расчет балок на прочность при плоском изгибе
 Скачать 2.53 Mb.
|
|
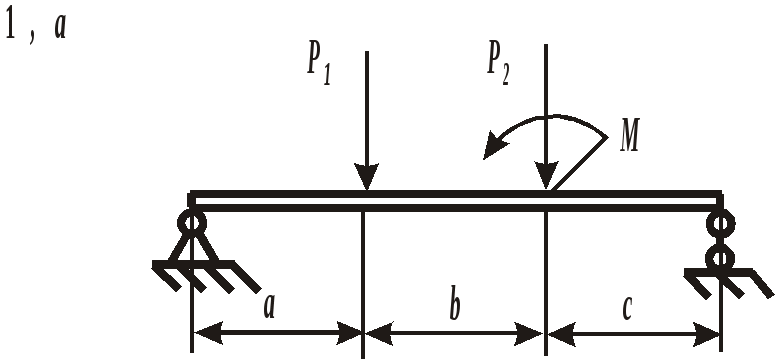
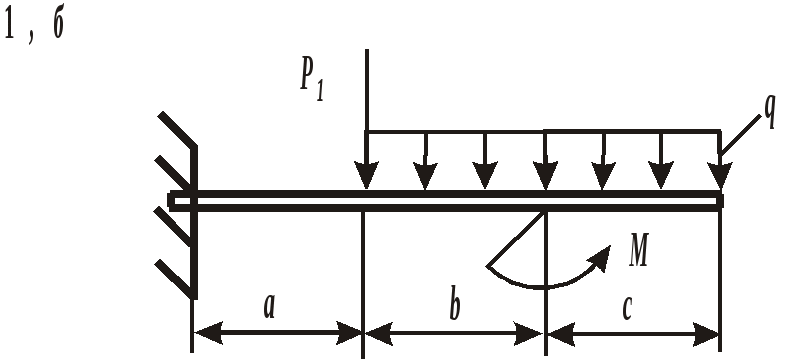
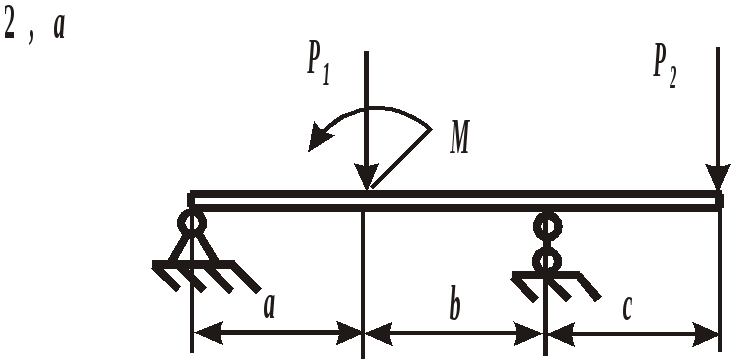
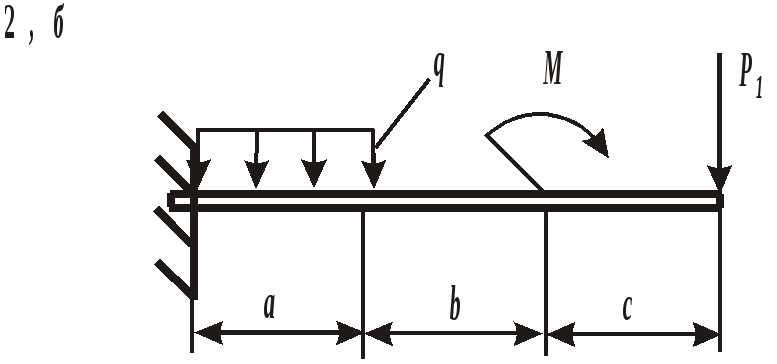
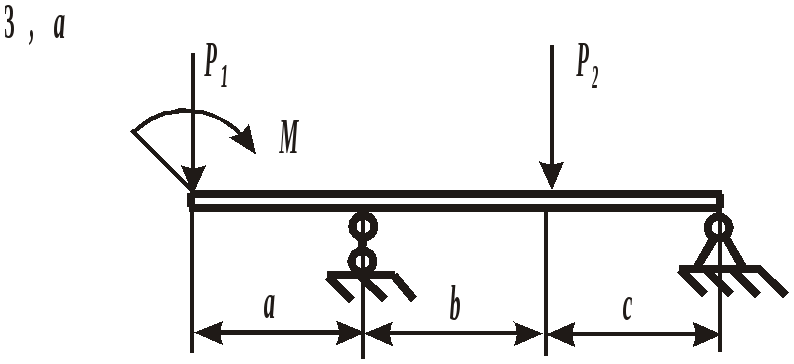
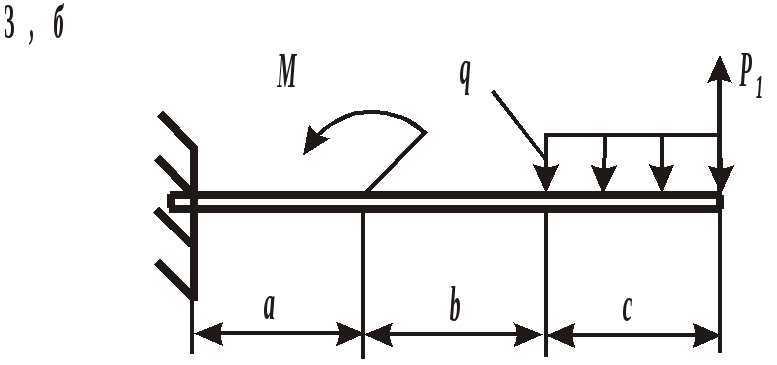
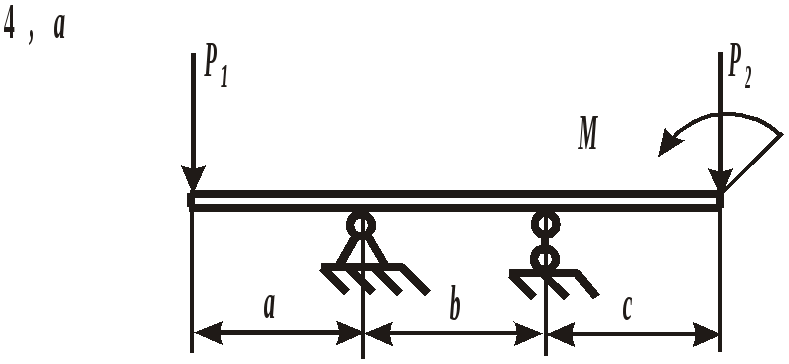
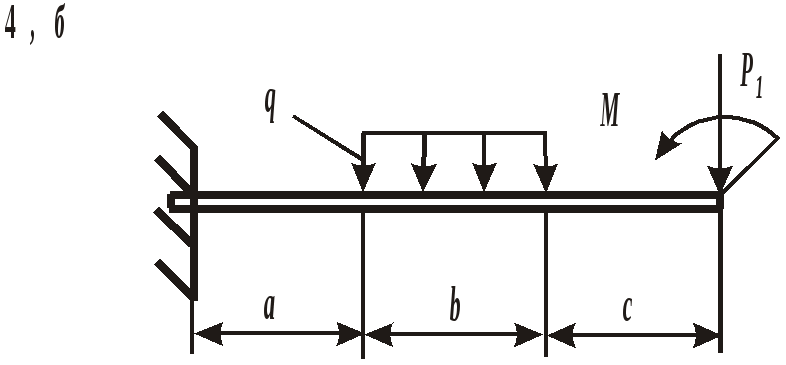
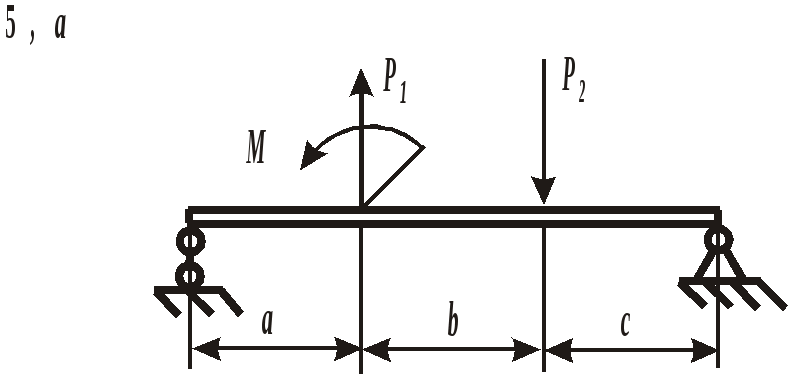
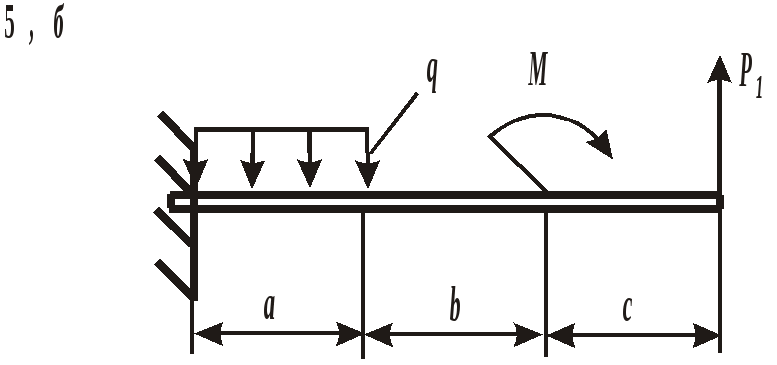
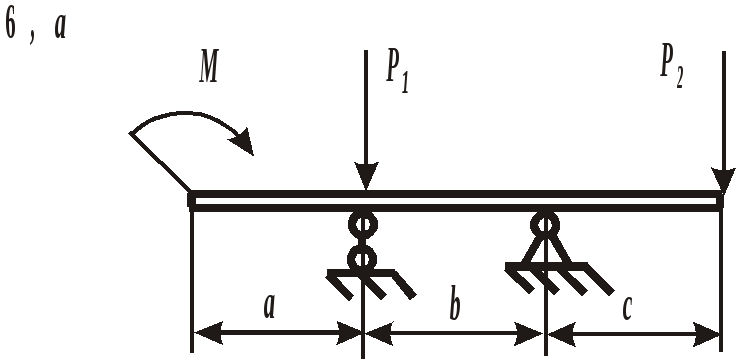
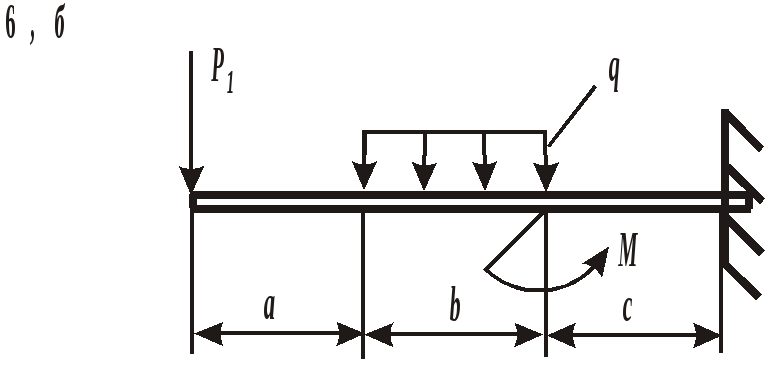
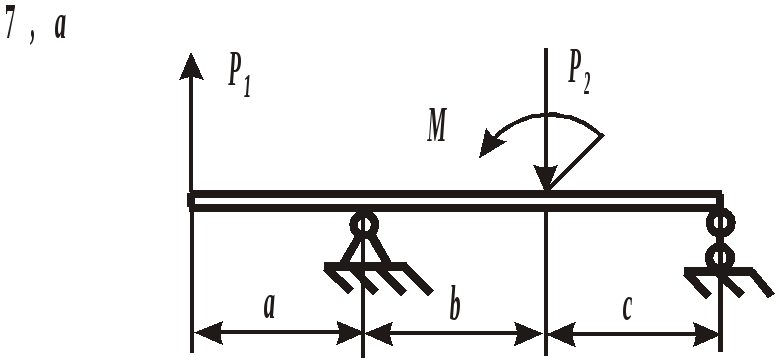
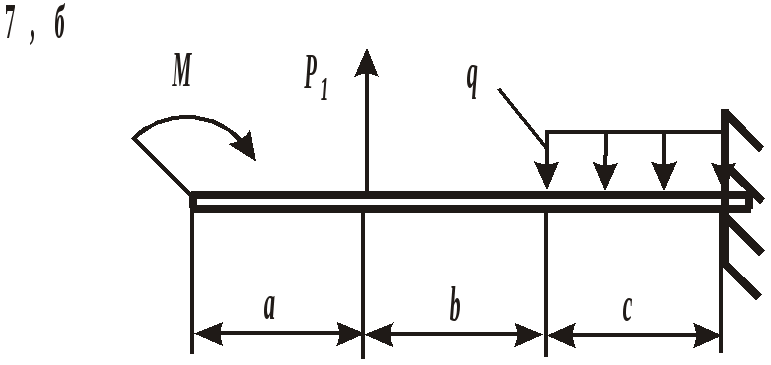
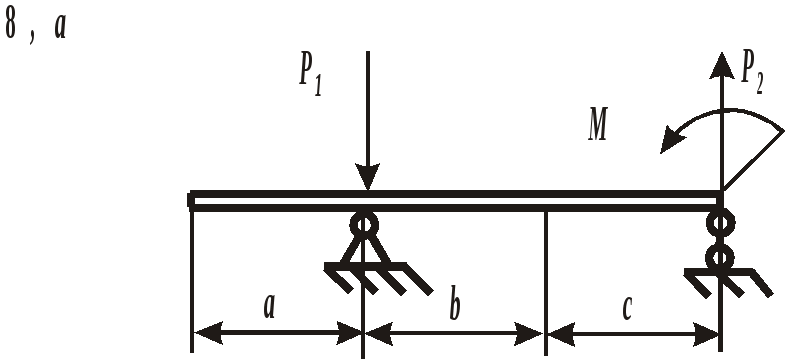
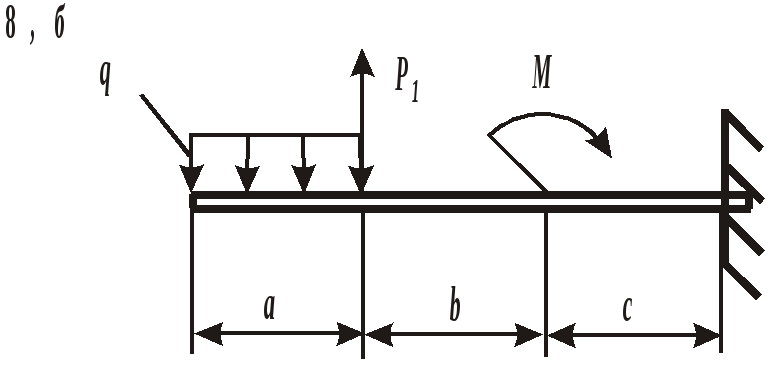
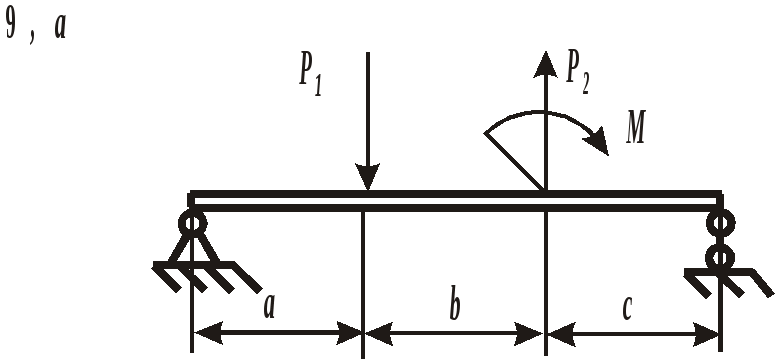
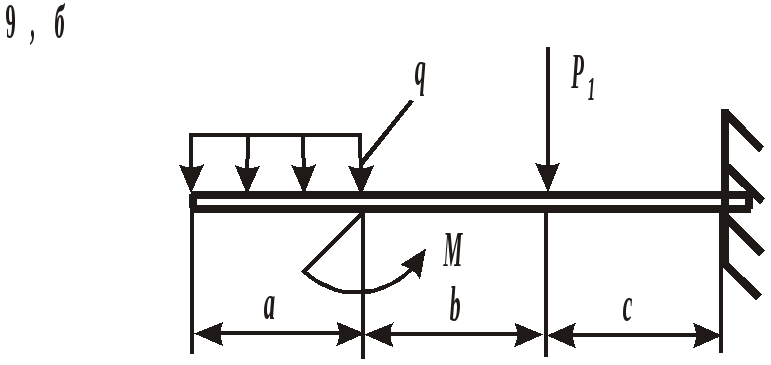
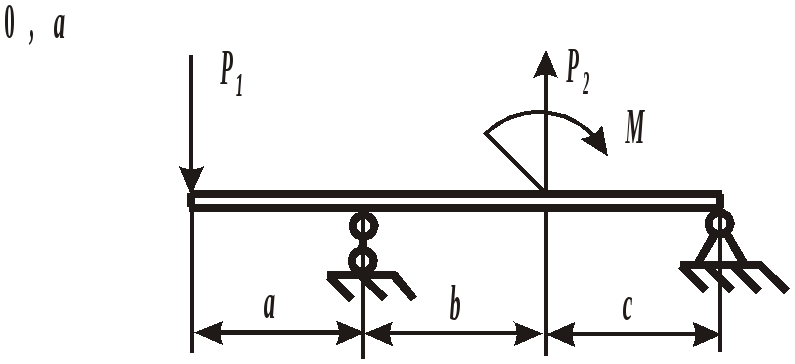
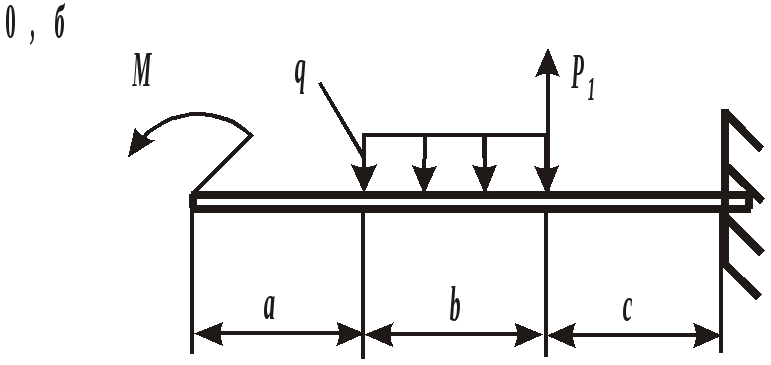
ЗАДАНИЕ 3. РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ Стальная балка постоянного поперечного сечения нагружена двумя силами Р1 , Р2и внешним изгибающим моментом М (схема а на рис. 11 и 12) или силой Р1 , моментом М и распределенной нагрузкой интенсивностью q (схема б на рис. 11 и 12). Требуется: – определить реакции опор, выполнив проверку полученных значений; – построить эпюры поперечных сил и изгибающих моментов, записав их аналитическое выражение для каждого из участков; – определить положение опасного сечения балки и внутренние силовые факторы, действующие в нем; – из расчета на прочность по нормальным напряжениям при изгибе подобрать для каждой схемы нагружения размеры поперечного сечения для трех вариантов изготовления балки (для схемы а поперечное сечение имеет вид круга диаметром d, прямоугольника с определенным соотношением высоты h и ширины b, двутавра, а для схемы б – кольца с заданным отношением внутреннего d и наружного D диаметров, квадрата и швеллера); – сравнить массы полученных для каждой схемы балок и выбрать наиболее экономичное сечение. Геометрические характеристики сечений приведены в приложении. Номер схемы соответствует последней цифре варианта, а номер строки в таблице 3 – первой цифре варианта. Таблица 3 Исходные данные для расчета балки при изгибе
Рис. 11. Схемы нагружения балок
Рис. 12. Схемы нагружения балок Пример выполнения задания. Дано: схема балки (рис. 13);  На изгиб работают балки, валы, оси и другие детали различных конструкций. В качестве примера можно привести межэтажные перекрытия зданий и сооружений, консольные балки балконов и козырьков, мостовые балки и т. п. В данной работе рассмотрен изгиб брусьев, имеющих хотя бы одну плоскость симметрии, а плоскость действия нагрузок совпадает с ней. При поперечном изгибе в любом поперечном сечении возникают деформации растяжения и сжатия, сдвига. Основой расчета на прочность большинства балок является расчет по нормальным напряжениям. В отличие от деформаций при центральном растяжении и сжатии напряжения, возникающие при поперечном изгибе, неравномерно распределяются по площади поперечного сечения и зависят не только от его площади, но и от формы сечения. Поэтому для экономически обоснованного расчета необходимо выбрать рациональные размеры и форму сечения. 1. Определение реакций опор балки от заданной нагрузки. Покажем внешние силы, приложенные к ферме: пары сил с моментами  и  ; силу Р; распределенную нагрузку интенсивностью q и реакции опор А и В (рис. 13).Реакция в опоре А (шарнирно-неподвижная опора) раскладывается на две составляющие – ZАи YА; в точке В реакция направлена перпендикулярно поверхности установки катка – RB. Составим уравнения равновесия сил, приложенных к ферме: 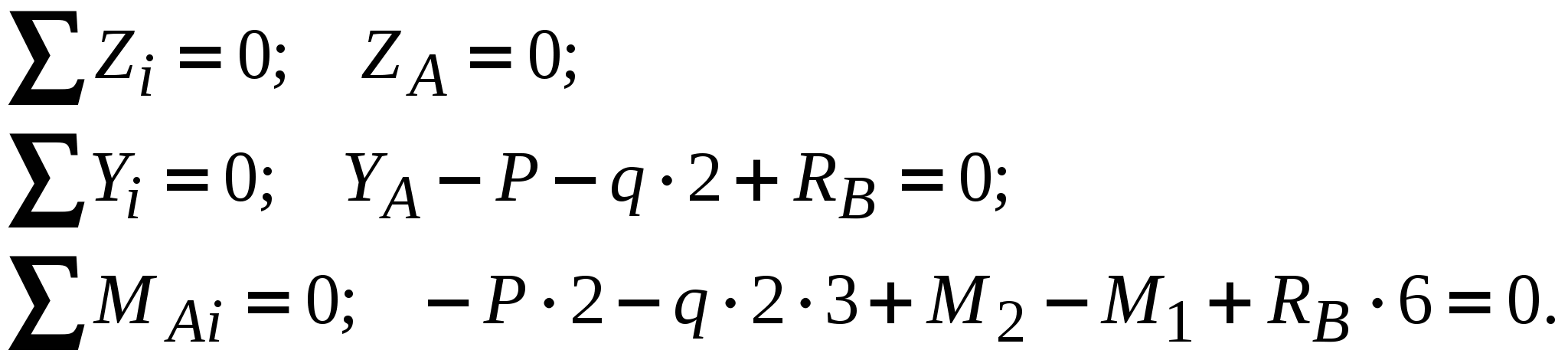 Из этих уравнений ZА= 0 кН;YА = 30 кН; RB = 30 кН. Для проверки правильности вычислений составим уравнение моментов сил относительно точки В:  то есть реакции опор найдены верно. Расчетная схема балки приведена на рис. 14. 2. Построение эпюр поперечных сил Q и изгибающих моментов  .Разбиваем балку на участки. За границы участков принимаются сечения, в которых приложены сосредоточенные силы, моменты и начинает или заканчивает действие распределенная нагрузка. Рассматриваемая балка делится на три участка. Запишем уравнения для определения внутренних силовых факторов для каждого из участков. 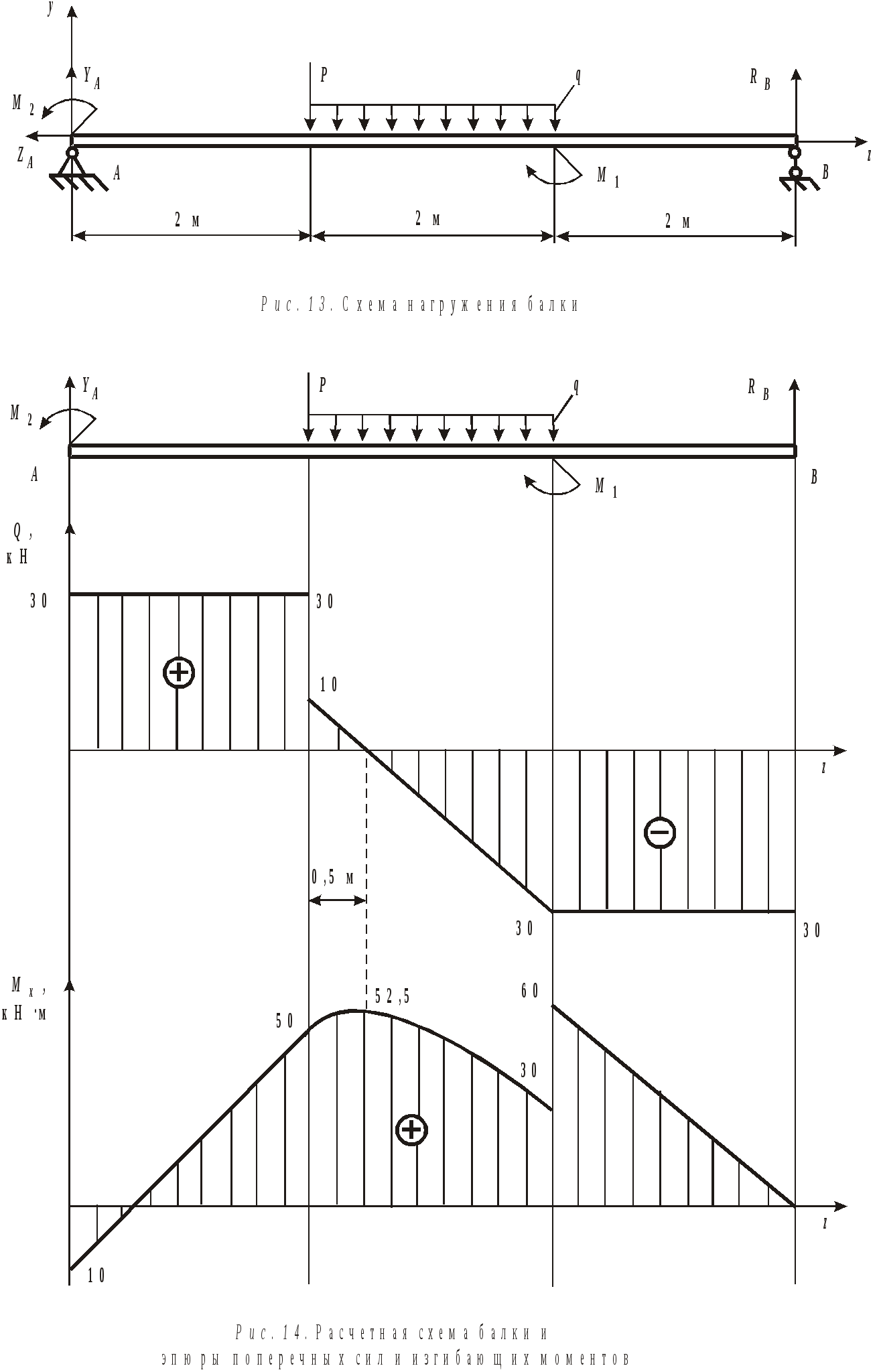 I 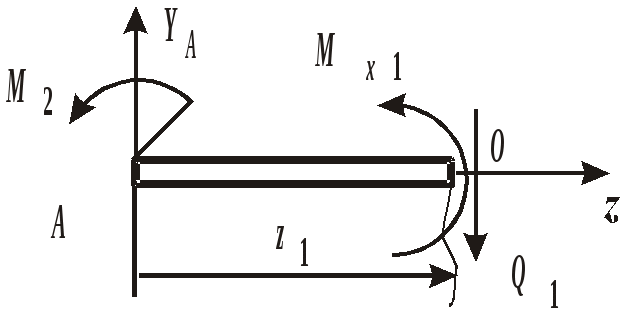 участок ( ): Рис.15. Участок I Отсюда  На границах участка: при  м  при   II участок ( 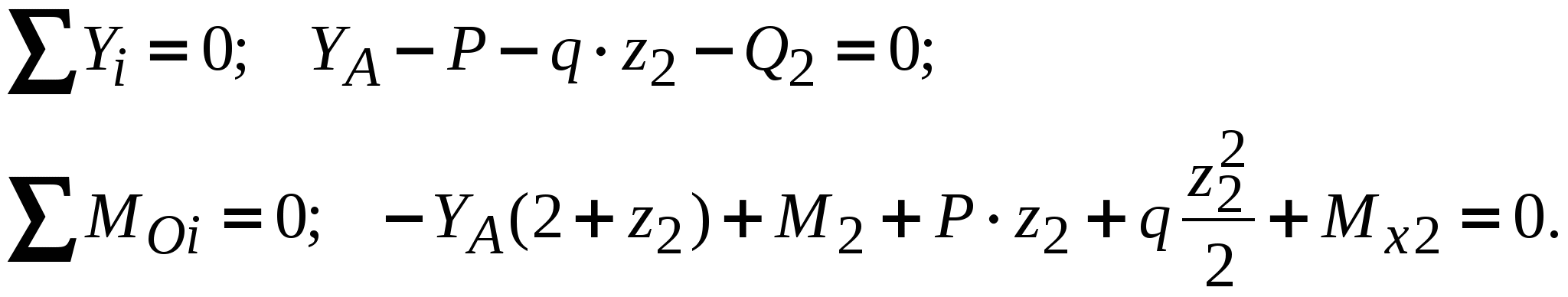 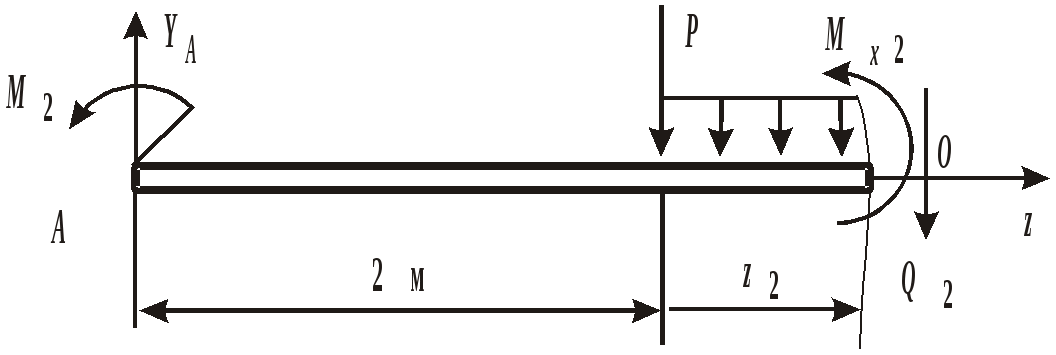):  Рис. 16. Участок II Отсюда  На границах участка: при   при   Так как поперечная сила Q2 на участке меняет знак, то эпюра изгибающего момента в этом сечении имеет минимум или максимум. При Q2= 0 координата  м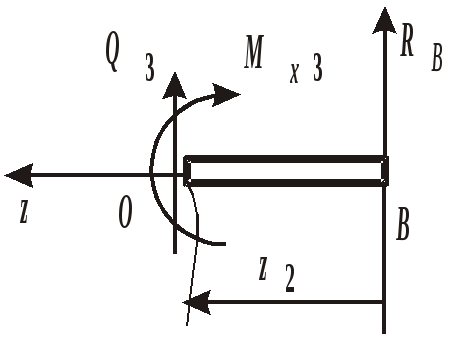. Значение изгибающего момента в этом сечении:  I  II участок ( ): Рис. 17. Участок III Отсюда  На границах участка: при  м  при   По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 14). 3. Определение положения опасного сечения. Опасное сечение расположено в том месте, где модуль изгибающего момента имеет максимальное значение. В рассмотренном примере оно расположено на границе второго и третьего участков, где  4. Определение расчетного осевого момента сопротивления сечения. Из условия прочности по нормальным напряжениям  находим расчетный осевой момент сопротивления сечения балки с учетом того, что [σ] = 190 МПа: 
5.1. Круг: 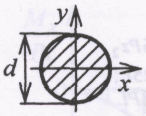 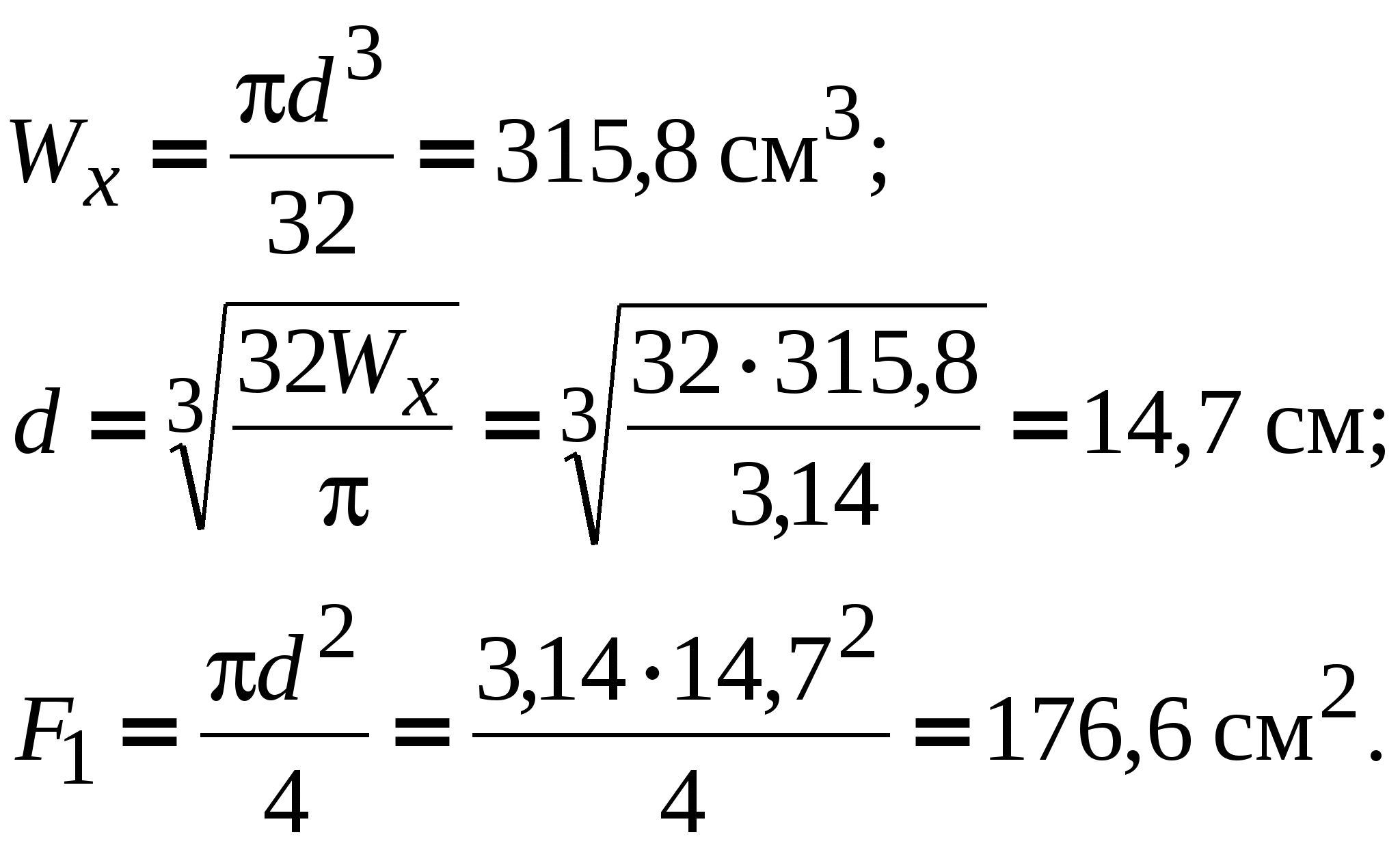 5.2. Квадрат: 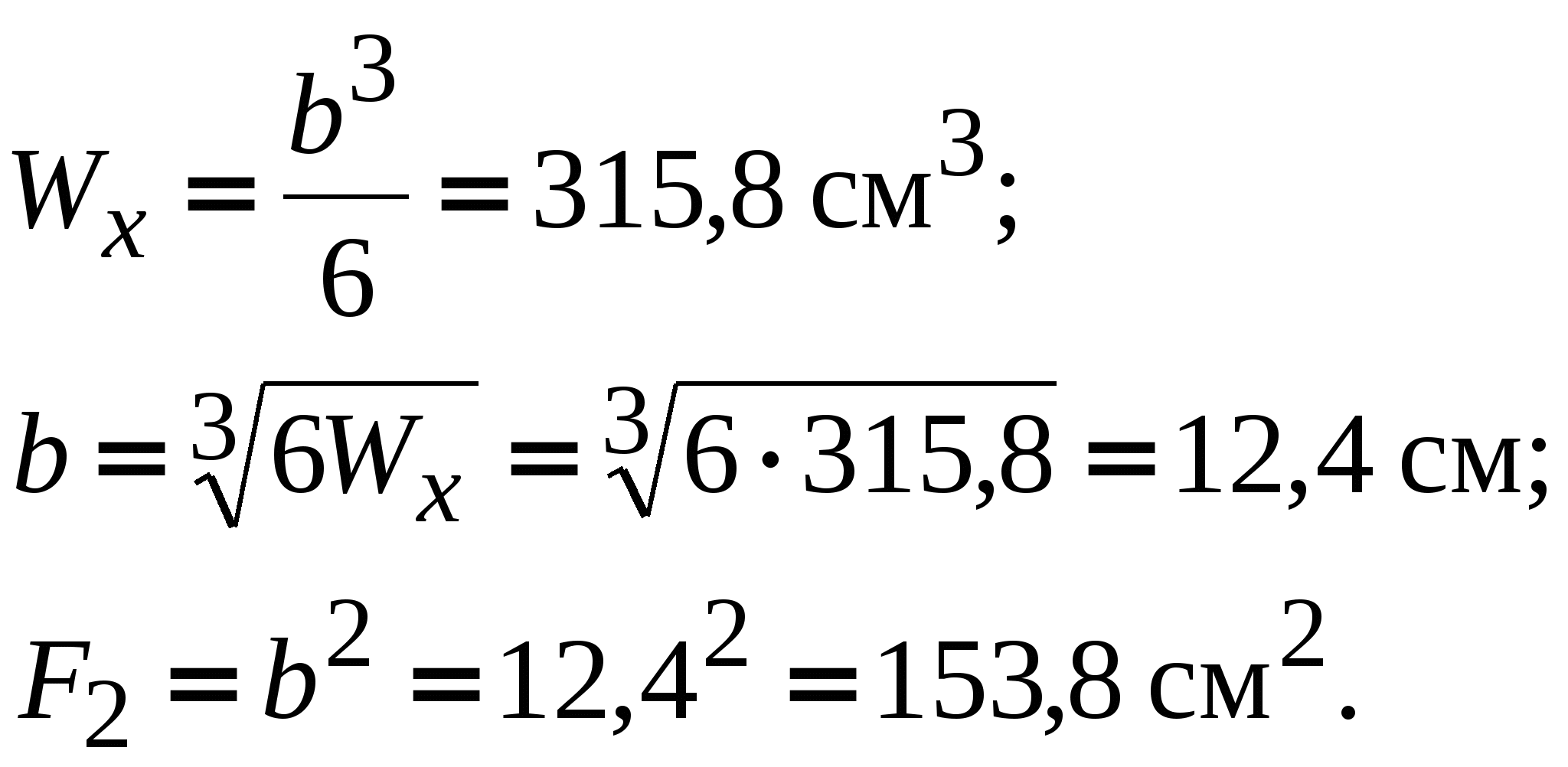  5.3. Прямоугольник с соотношением сторон h/b = 2: 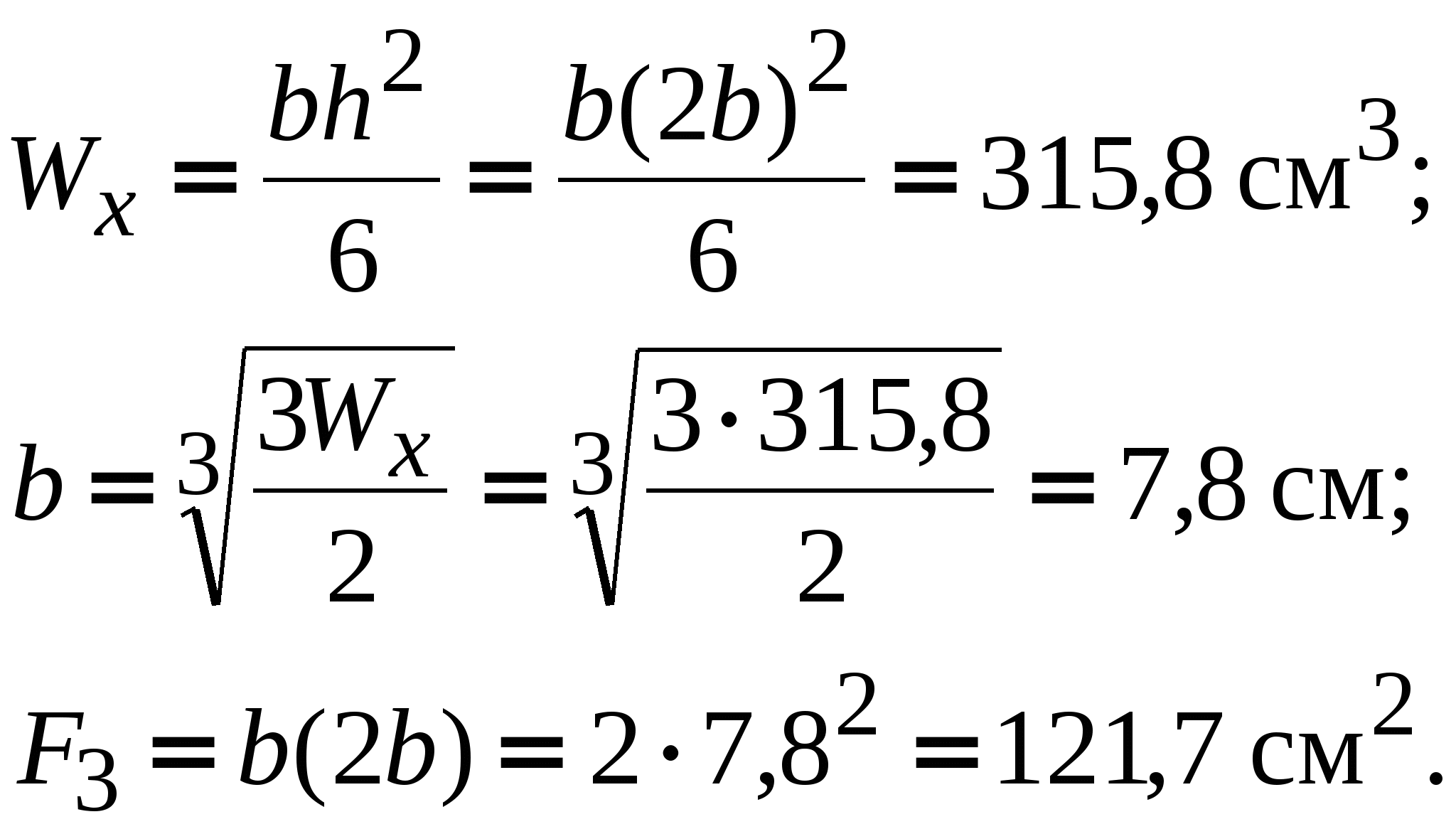 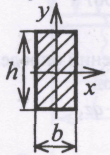 5.4. Кольцо с соотношением α = d/D = 0,7: 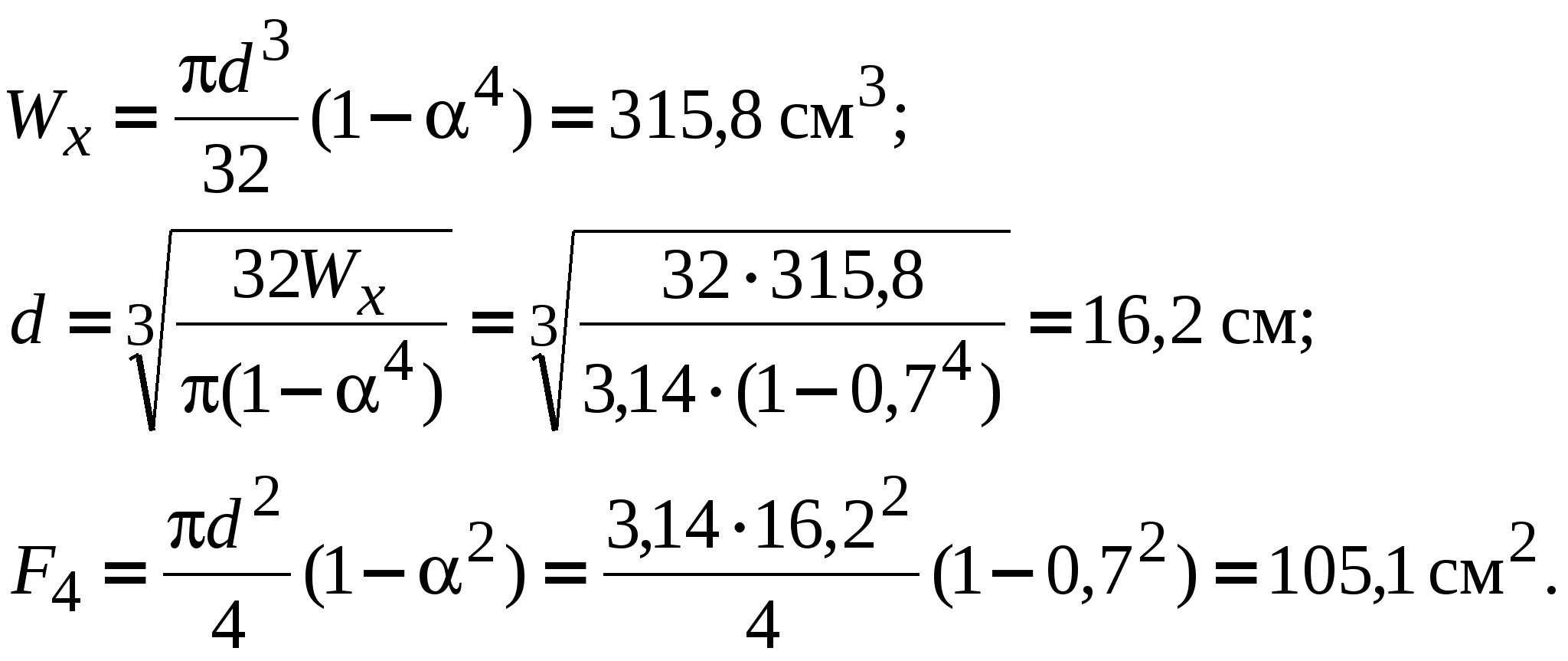 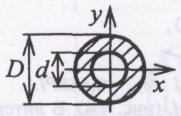 5 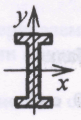 .5. Двутавр: по таблице сортамента прокатной стали (ГОСТ 8239 – 89) подбираем двутавровое сечение с моментом сопротивления большим или равным расчетному. В данном случае это двутавр №27, у которого 
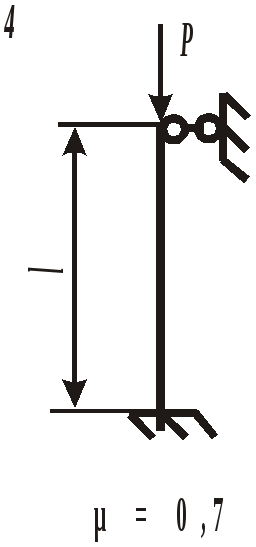
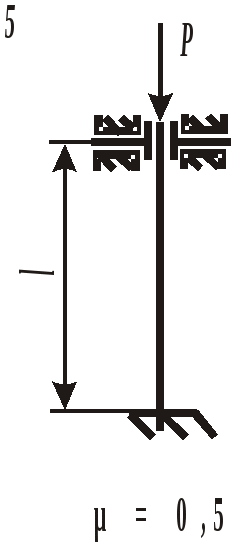
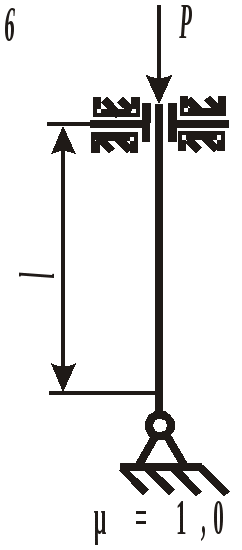
Для выбора наиболее экономичного варианта изготовления сравним массы балок различного поперечного сечения. При прочих равных условиях массы балок относятся так же, как и площади их поперечных сечений:  Таким образом, наиболее выгодной является балка двутаврового сечения, масса которой, а следовательно, и стоимость, в 4,39 раза меньше, чем у балки круглого сечения. ЗАДАНИЕ 4.РАСЧЕТ КОЛОННЫ НА УСТОЙЧИВОСТЬДля заданной расчетной схемы колонны (рис. 18), изготовленной из стали Ст. 3 (  ) и имеющей составное сечение (рис.19), определить допускаемую нагрузку при заданном коэффициенте запаса устойчивости  . Профили составного сечения расположены вплотную друг к другу.При расчетах принять значения гибкости для материала колонны:  .Если   критическое напряжение определяется по формуле Эйлера: .Если  критическое напряжение вычисляется по формуле Ясинского:  ,где коэффициенты а =310 МПа и b =1,14 МПа. При  критическое напряжение равно пределу текучести  .Расчетная схема колонны (рис. 18) и строка в таблице 4 с исходными данными соответствуют первой цифре варианта, а вид составного сечения (рис. 19) – последней цифре варианта. Таблица 4 Исходные данные для расчета колонны
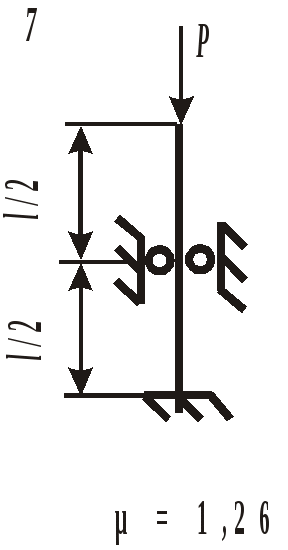
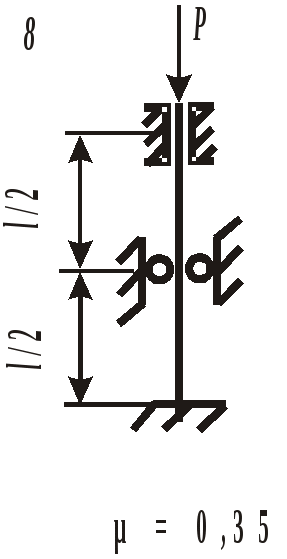
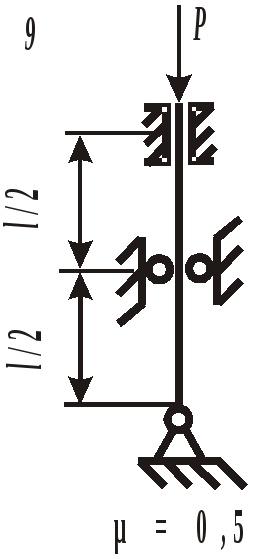
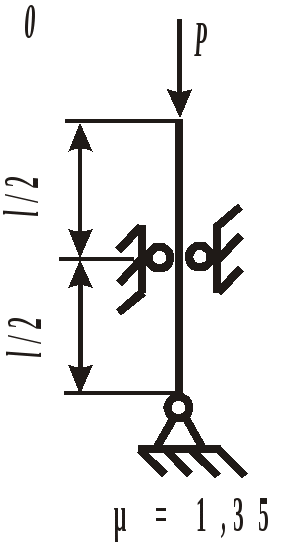
Рис. 18. Расчетная схема колонны
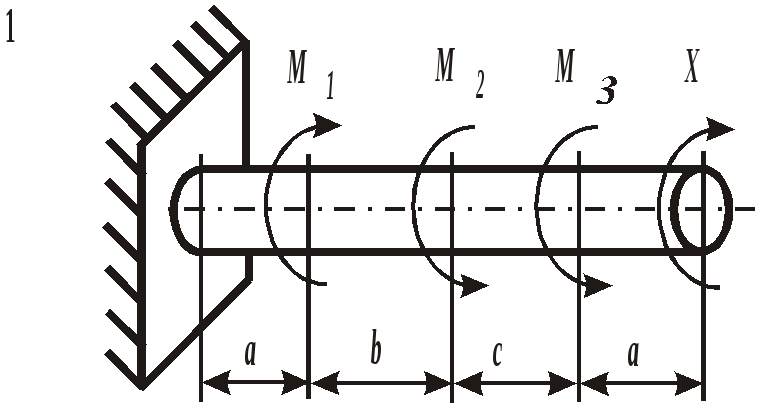
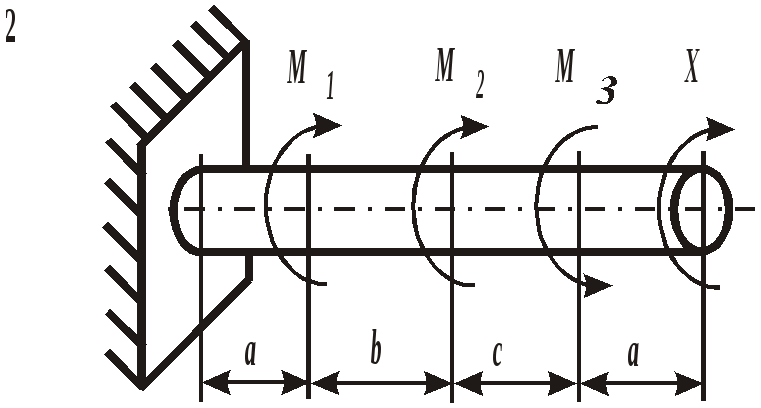
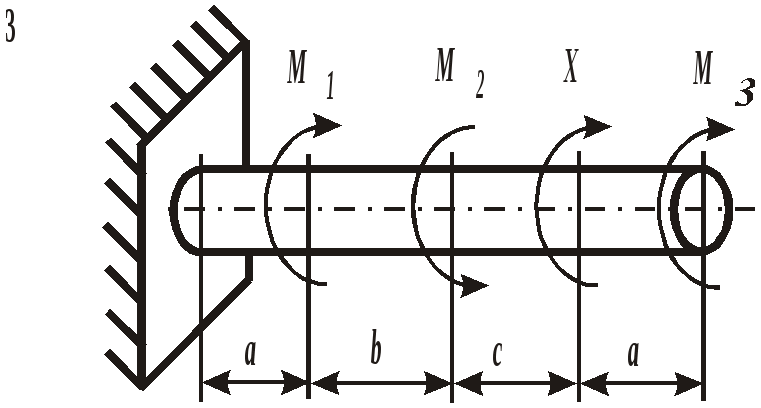
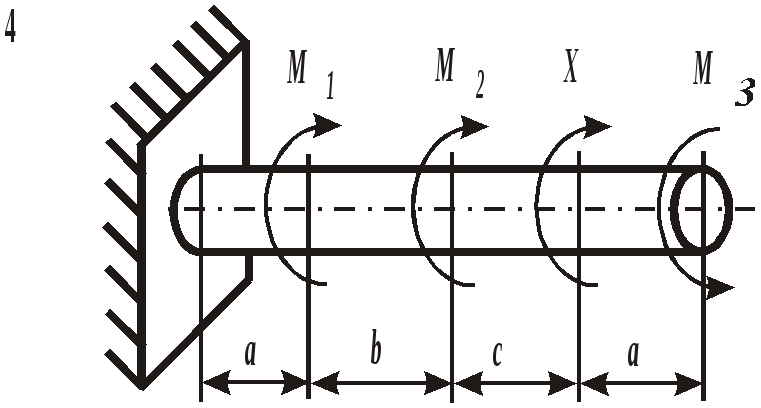
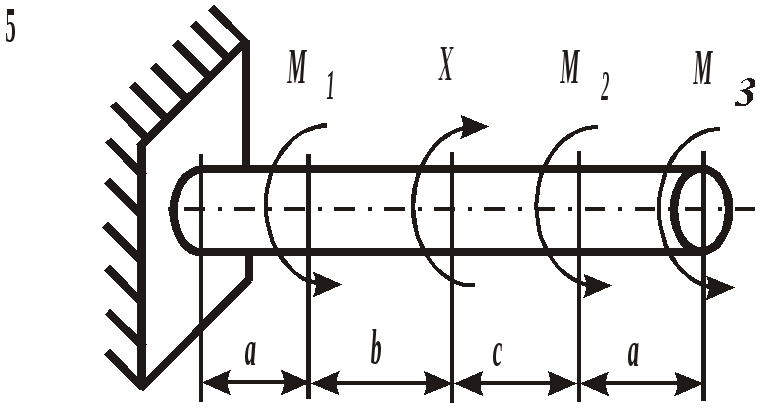
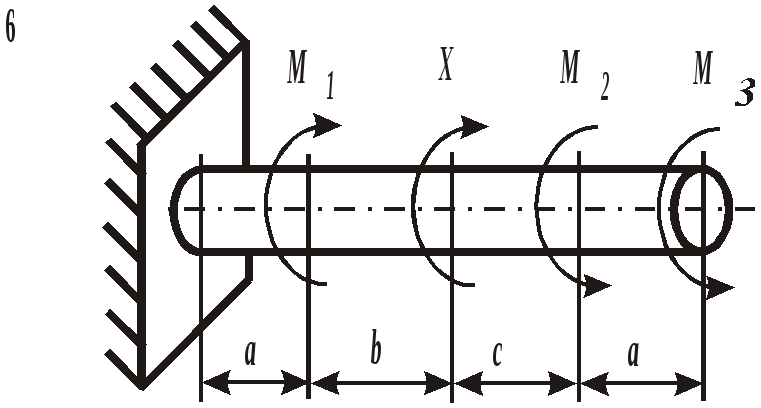
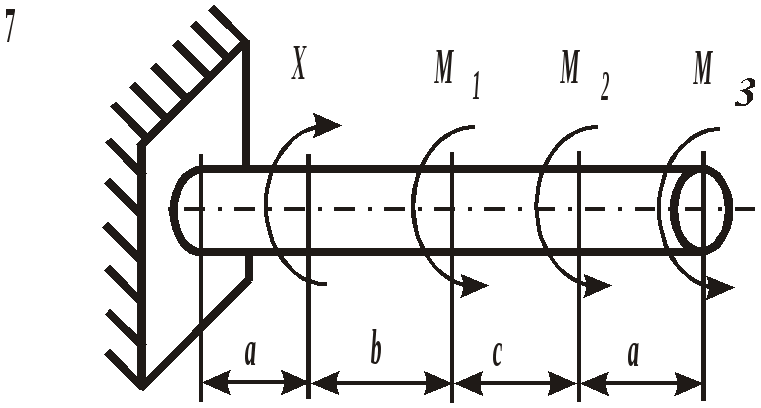
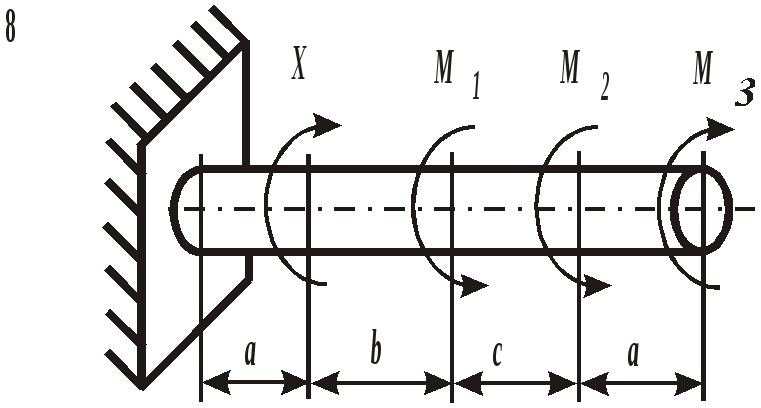
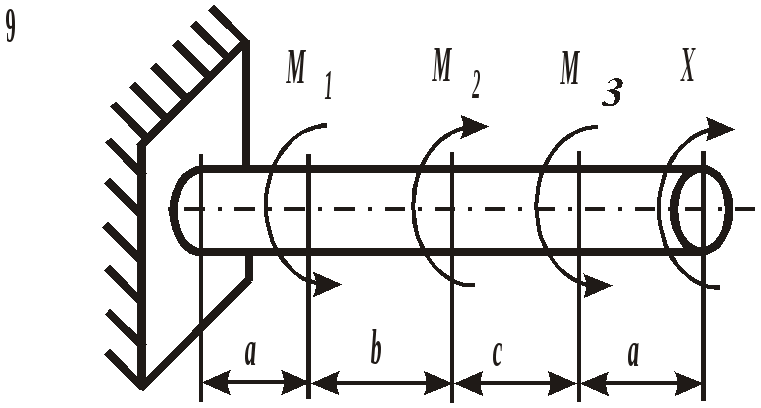
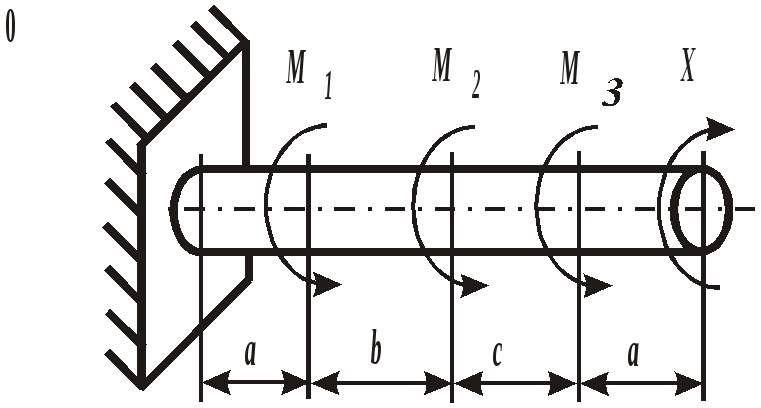
Рис. 19. Вид составного сечения Пример выполнения задания. Дано: две схемы нагружения колонны высотой 5 метров (рис.20), изготовленной из стали Ст. 3 и имеющей составное сечение из швеллера №16 и двух равнобоких уголков  (рис. 21). Определить допускаемую нагрузку при заданном коэффициенте запаса устойчивости = 4. Продольным изгибом называется изгиб первоначально прямолинейного стержня вследствие потери устойчивости под действием центрально приложенных сжимающих сил. Нагрузки, превышение которых приводит к потере устойчивости, называются критическими. Если нагрузки не превышают этого значения, то стержень остается прямолинейным, испытывая только деформации сжатия. Искривленный стержень испытывает сочетание деформаций центрального сжатия и изгиба, которые могут угрожать прочности конструкции. Поэтому критическое состояние считается недопустимым. Опасность потери устойчивости особенно актуальна в настоящее время в связи с широким использованием тонкостенных элементов конструкций типа стержней, балок, пластин и оболочек, изготовленных из высокопрочных материалов. Расчет на устойчивость необходим, например, при проектировании ферм различного назначения, всевозможных вышек, башен и мачт, несущих конструкций зданий и сооружений.  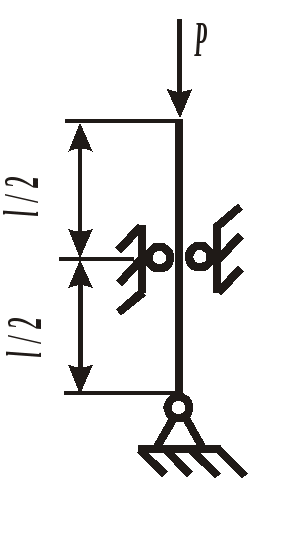  а) б) Рис. 20. Расчетные схемы нагружения колонны Рис. 21. Форма составного сечения 1. Основные геометрические характеристики составных частей сечения. Геометрические характеристики составных частей сечения определяются по таблице сортамента прокатной стали ГОСТ 8240 – 86 (швеллеры) и ГОСТ 8509 – 87 (равнобокий уголок): 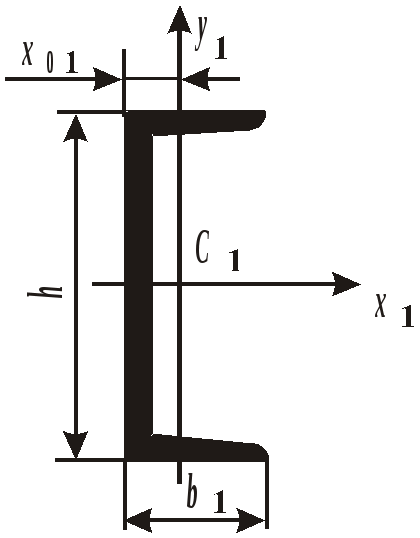 h = 16 см; b1 = 6,4 см; x01 = 1,79 см; Ix1 = 747 см4; Iy1 = 63,3 см4; F1 = 18,0 см2. 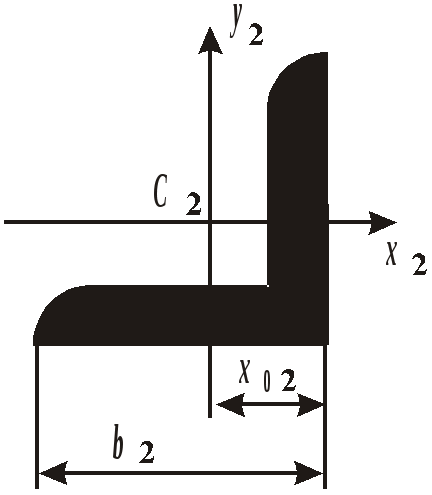 b2 = 8,0 см; x02 = y02 = 2,19 см; Ix2 = Iy2 = 57 см4; F2 = 9,38 см2. 2. Определение положения центра тяжести составного сечения. Определим положение центра тяжести всего сечения относительно произвольной системы координат xОy (рис. 22). Так как сечение имеет ось симметрии, то его центр тяжести расположен на этой оси, т. е. yC = 0. Координату xC определим по формуле  ,где  и 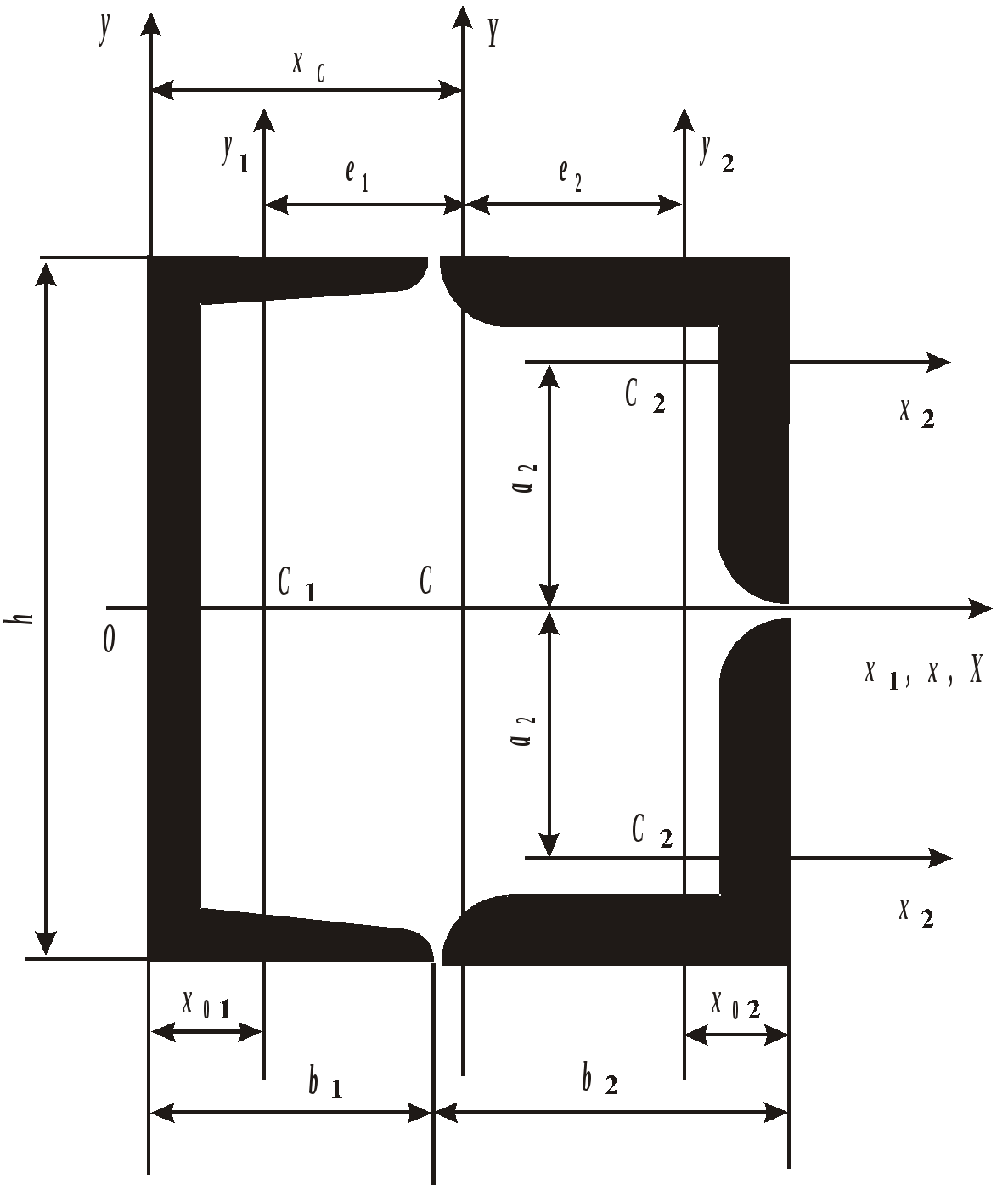 – площадь и координата центра тяжести каждой составной части сечения. см.Ч  ерез полученную точку проведем главные центральные оси инерции сечения X и Y. Рис. 22. Расчетная схема сечения 3. Определение минимального осевого момента инерции сечения. Для нахождения моментов инерции составного сечения воспользуемся теоремой о моментах инерции относительно параллельных осей, согласно которой  где  – моменты инерции составных частей сечения относительно собственных центральных осей, параллельных главным центральным осям инерции всего сечения; – расстояния между соответствующими осями отдельных составных частей и осями всего сечения в целом.В рассматриваемом примере:  см;  см; см; см.Тогда  см4; см4.Из двух осевых моментов инерции выбираем минимальный, так как именно вокруг этой оси будет поворачиваться сечение при продольном изгибе: Imin = IY= 368,7 см4. 4. Определение минимального радиуса инерции сечения. imin 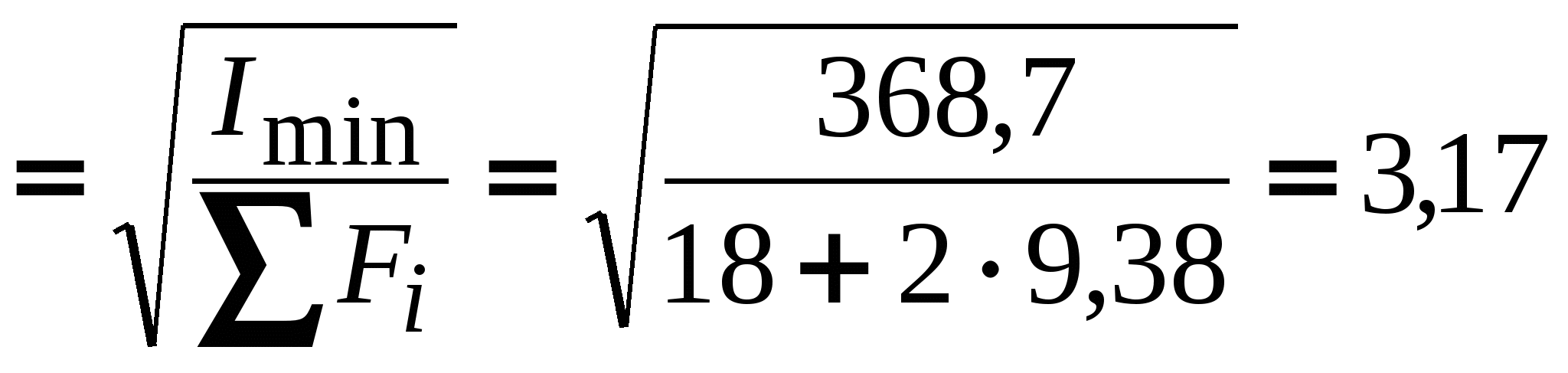 см.5. Определение гибкости колонны. Гибкость колонны (λ) определяется только ее конструкцией и зависит от высоты (l), формы и размеров поперечного сечения (imin), а также от условий закрепления и отношения продольных размеров колонны (μ):  где μ – коэффициент приведения длины. Для схемы колонны, приведенной на рис. 20, а – μ = 0,5, а для схемы на рис. 20, б – μ = 1,35. Тогда: а)  ;б)  6. Определение критических напряжений. Так как в случае а) гибкость колонны находится в интервале  , то критическое напряжение определяется по эмпирической формуле Ясинского:  В случае б) гибкость колонны больше критической (  ), поэтому критическое напряжение вычисляем по формуле Эйлера, приняв модуль продольной упругости материала  : 43,5 МПа.7. Определение критической силы. Критическая сила определяется, исходя из деформации сжатия: Ркр = σкрF, где F  – площадь поперечного сечения колонны.а) Ркр =  Н = 808,72 кН;б) Ркр =  Н = 159,91 кН.8. Определение допускаемой нагрузки. Любая конструкция не должна работать при нагрузках, близких к критическим. Поэтому допускаемая ее величина должна быть меньше критической в несколько раз, что определяется коэффициентом запаса устойчивости :а)  Ркр/ =808,72/4 = 202,18 кН;б) Ркр/ =159,91/4 = 39,98 кН.Таким образом, изменяя только способ закрепления колонны при прочих равных условиях, можно добиться повышения ее несущей способности практически в пять раз для схемы а) по сравнению со схемой б). При проектировании следует иметь ввиду, что наиболее экономичными с точки зрения расхода материала являются колонны, стержни и мачты с кольцевым или коробчатым поперечным сечением. ЗАДАНИЕ 5. РАСЧЕТЫ ВАЛА С КРУГЛЫМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ Круглый стальной вал постоянного поперечного сечения, жестко закрепленный на одном конце, нагружен тремя известными внешними крутящими моментами М1, М2, М3и неизвестным моментом Х (рис. 6). Требуется:
При расчетах принять модуль сдвига для материла вала G=  МПа, допускаемый угол закручивания поперечного сечения – [φ] = 0,2 град. Другие данные, необходимые для расчета, приведены в таблице 5, а схемы нагружения валов – на рис. 6.Номер схемы соответствует последней цифре варианта, а номер строки в таблице 5 – первой цифре варианта. Таблица 5 Исходные данные для расчета валов
Рис. 6. Схемы нагружения валов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
