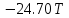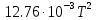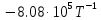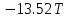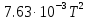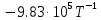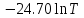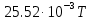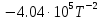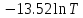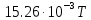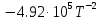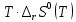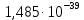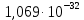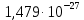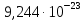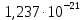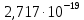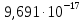Термодинамика. Яковлева Д.Д. Приклодная термодинамика 2. Расчет химического равновесия по табличным термодинамическим данным Формулировка задачи
 Скачать 70.31 Kb. Скачать 70.31 Kb.
|
|
Расчет химического равновесия по табличным термодинамическим данным 1. Формулировка задачи По термодинамическим данным для реакции (реакция взята из приложения А1): 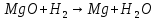 (I) (I)В интервале температур 600 – 1300 К рассчитать изменения функций 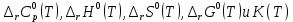 . Построить графики этих функций с температурным шагом 100 градусов. Проанализировать изменение этих функций при росте температуры. Рассчитать равновесный состав газовой фазы при условии, что общее давление равно 1 атм. Сделать заключение о направленности реакции в расчетном интервале температур. . Построить графики этих функций с температурным шагом 100 градусов. Проанализировать изменение этих функций при росте температуры. Рассчитать равновесный состав газовой фазы при условии, что общее давление равно 1 атм. Сделать заключение о направленности реакции в расчетном интервале температур.2. Составление таблицы термодинамических данных Из приложения А2 сделать выборку термодинамических данных веществ реакции и поместить их в таблицу 1. Табличные данные показывают, что в интервале температур 600 – 1300 К происходит фазовое превращение твердого кадмия. При температуре 932 К твердая фаза перестраивается в жидкую фазу. Следовательно, расчету подлежат две химические реакции: 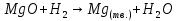 в интервале 600 – 923 К. (II) в интервале 600 – 923 К. (II) в интервале 923 – 1300 К. (III) в интервале 923 – 1300 К. (III)Таблица 1 – Термодинамические данные веществ реакции (I)
3. Расчет изменения теплоемкости 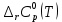 Изменения теплоемкости 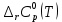 реакций (II) и (III) определяются уравнениями: реакций (II) и (III) определяются уравнениями: 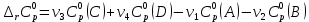 для интервала от стандартной температуры (Т=298К) до температуры фазового перехода (Т=Тф.п.) и для интервала от стандартной температуры (Т=298К) до температуры фазового перехода (Т=Тф.п.) и 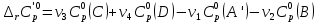 для интервала от Тф.п. до конечной температуры Т. Подстановка в них табличных данных дает следующие температурные зависимости: для интервала от Тф.п. до конечной температуры Т. Подстановка в них табличных данных дает следующие температурные зависимости: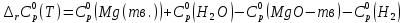 . .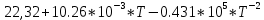 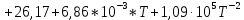 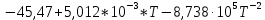  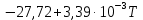 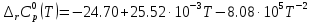 , Дж/К (1) , Дж/К (1)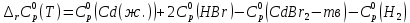 . .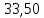 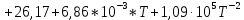 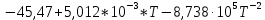 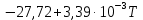  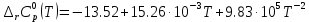 , Дж/К (2) , Дж/К (2)Уравнения (1) и (2) описывают реакции (II) и (III) и отвечают равенствам 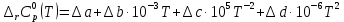 и и 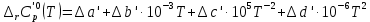 без последнего слагаемого, так как для этих реакций без последнего слагаемого, так как для этих реакций 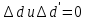 . Сравнение уравнений (1) и (2) показывает, что фазовое превращение одного из веществ, приводит к изменению термодинамической характеристики реакций. . Сравнение уравнений (1) и (2) показывает, что фазовое превращение одного из веществ, приводит к изменению термодинамической характеристики реакций. Расчет по уравнениям (1) и (2) представим таблицей 2 и графиком (рисунок 1). Таблица 2 – Расчетные значения 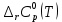 и и 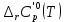 реакции (I) реакции (I)
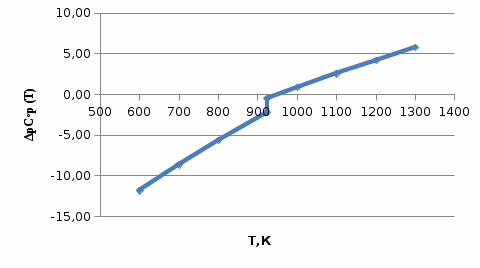 Рисунок 1 – Зависимость изменения теплоемкости реакции (I) от температуры 4. Расчет изменения энтальпии 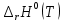 Изменение энтальпии реакции (I) описывается уравнением 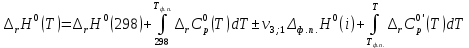 . В расчете учитываем, что в температурном интервале 600-1300 К протекают реакции (II) и (III). Это позволяет общее уравнение . В расчете учитываем, что в температурном интервале 600-1300 К протекают реакции (II) и (III). Это позволяет общее уравнение 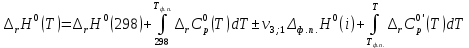 представить двумя частями: представить двумя частями: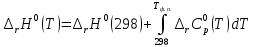 (3) (3)Для интервала 600-923 К. 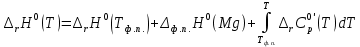 (4) (4)Для интервала 923-1300 К. В равенстве (4) эффект фазового превращения кадмия прибавляется, так как это вещество является продуктом. Видно, что необходимо определить 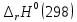 по уравнению по уравнению 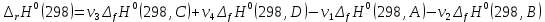 и далее раскрыть интегральные уравнения: и далее раскрыть интегральные уравнения: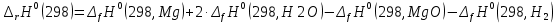 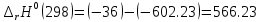 кДж кДж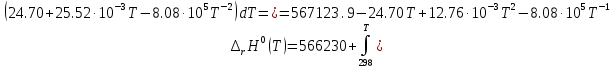 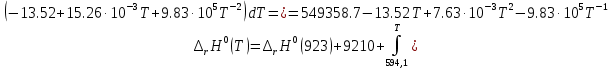 Представляем расчет таблицей 3 и графиком (рисунок 2). По условию задачи считать будем с 850 К. Таблица 3 – Расчетные значения 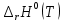 реакции (I) реакции (I)
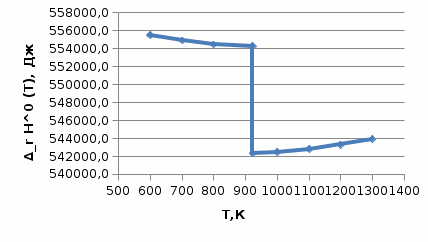 Рисунок 2 – Зависимость изменения энтальпии реакции (I) от температуры Анализ полученной зависимости сделаем с помощью закона Кирхгофа: 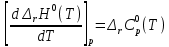 . Поведение функции при изменении аргумента определяется по знаку первой производной функции. Из рисунка 1 видно, что с ростом температуры . Поведение функции при изменении аргумента определяется по знаку первой производной функции. Из рисунка 1 видно, что с ростом температуры 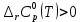 , поэтому , поэтому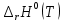 растет на всем интервале 600-1300 К. В точке разрыва (Т=923 К) растет на всем интервале 600-1300 К. В точке разрыва (Т=923 К) 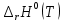 меняется скачком. меняется скачком.5. Расчет изменения энтропиии 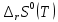 Изменение энтропии реакции (I) описывается уравнением 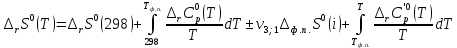 . Учитываем, что в интервале 600-1300 К протекают две реакции (II) и (III), поэтому изменение энтропии будем считать по двум уравнениям, следующим из равенства . Учитываем, что в интервале 600-1300 К протекают две реакции (II) и (III), поэтому изменение энтропии будем считать по двум уравнениям, следующим из равенства 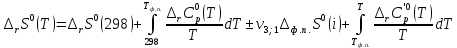 : :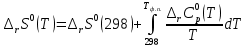 (5) (5)для интервала 600-923 К. 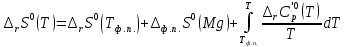 (6) (6)для интервала 923-1300 К. По уравнению 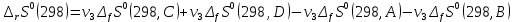 определяем определяем 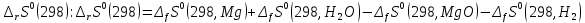 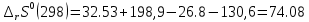 Дж/К Дж/К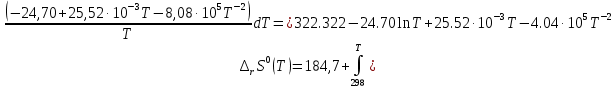 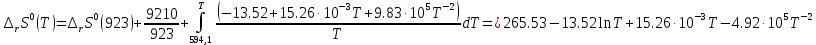 Расчет по уравнениям (5) и (6) представим таблицей 4 и графиком (рисунок 3). Таблица 4 – Расчетные значения 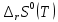 реакции (I) реакции (I)
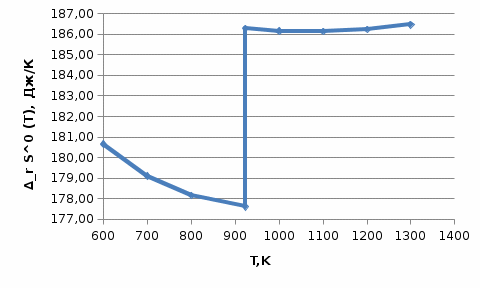 Рисунок 3 – Зависимость изменения энтропии реакции (I) от температуры Сравним графики рисунков 2 и 3. Видим, что поведение обеих функций - 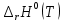 и и 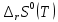 при изменении температуры подобно. Так и должно быть, так как обе функции описываются изменением теплоемкости реакции. при изменении температуры подобно. Так и должно быть, так как обе функции описываются изменением теплоемкости реакции.6. Расчет изменения энергии Гиббса 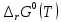 Изменение энергии Гиббса реакции (I) описывается уравнением 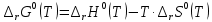 . Расчет представим таблицей 5 и графиком (рисунок 4). Обратим внимание на то, что функция . Расчет представим таблицей 5 и графиком (рисунок 4). Обратим внимание на то, что функция 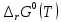 не претерпевает разрыва при температуре фазового превращения в отличие от функций не претерпевает разрыва при температуре фазового превращения в отличие от функций 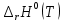 и и 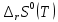 . Это верно и следует из уравнения . Это верно и следует из уравнения 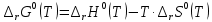 , записанного для температуры фазового перехода: , записанного для температуры фазового перехода: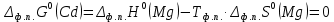 Таблица 5 – Расчетные значения 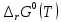 реакции (I) реакции (I)
Для анализа полученной зависимости нужно воспользоваться следующим дифференциальным уравнением: 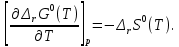 (7) (7)В нашем расчете изменение энтропии реакции (I) во всем расчетном интервале температур больше нуля. Следовательно, производная уравнения (7) отрицательна, что делает 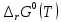 убывающей функцией при росте температуры. Рисунок 4 это иллюстрирует. убывающей функцией при росте температуры. Рисунок 4 это иллюстрирует.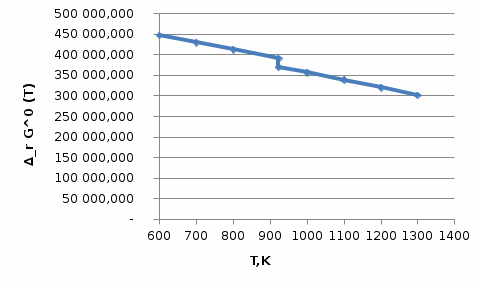 Рисунок 4 – Зависимость изменения энергии Гиббса реакции (I) от температуры 7. Расчет константы равновесия Константа равновесия реакции (I) определяется из уравнения 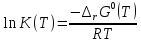 . Расчет представим таблицей 6 и графиком (рисунок 5). . Расчет представим таблицей 6 и графиком (рисунок 5).Таблица 6 – Расчетные значения 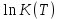 реакции (I) реакции (I)
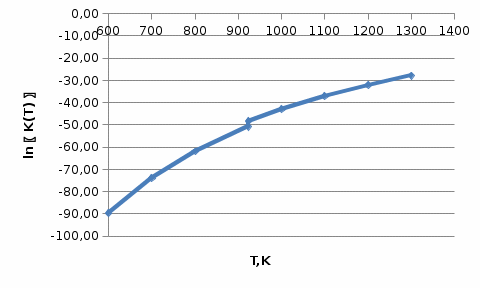 Рисунок 5 – Зависимость 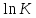 реакции (I) от температуры реакции (I) от температурыНа рисунке 5 изображена логарифмическая зависимость константы равновесия реакции (I) по двум причинам: во-первых, этот график более нагляден; во-вторых, температурная зависимость константы равновесия реакции (I) – логарифмическая и описывается уравнением Вант-Гоффа: 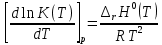 . (8) . (8)Анализируя уравнение (8) приминительно к реакции (I), подтверждаем результаты нашего расчета: константа равновесия должна быть возрастающей функцией при увеличении температуры, так как 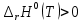 . .8. Расчет равновесного состава газовой фазы В реакции присутствует одно газообразное вещество. При условии, что обш=щее давление системы постоянно (1 атм), необходимость расчета газовой фазы отпадает. Давление газообразного участника реакции при любой температуре равно 1 атм. Расчет завершен. Поставленная задача выполнена. Для реакции 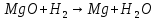 имеется весь набор термодинамических характеристик в интервале 600-1300 К и можно судить о ее направлении. имеется весь набор термодинамических характеристик в интервале 600-1300 К и можно судить о ее направлении. Самопроизвольность процесса при условии 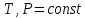 определяется по второму закону термодинамики для необратимых процессов: определяется по второму закону термодинамики для необратимых процессов: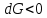 (9) (9)Неравенство (9) говорит о том, что если изменение энергии Гиббса положительно, то процесс в системе протекает обратимо. Обратимые процессы не могут протекать самопроизвольно в прямом направлении, однако обратная реакция идет самопроизвольно. Для системы с химической реакцией это означает, что исходные вещества не взаимодействуют друг с другом, и реакция протекает в обратном направлении. . 9. Вывод В интервале температур 600-1300 К изменение энергии Гиббса реакции M 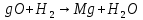 положительно. Реакция протекает в обратном направлении. положительно. Реакция протекает в обратном направлении.С практической точки зрения, на основании расчета, делаем следующее заключение: получить магний по реакции (I) можно, если систему нагреть до температуры не менее 600 К, а при 923 К магнийй изменит свое агрегатное состояние с твердого на жидкое. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

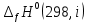
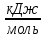
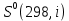
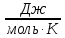
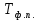
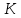
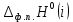
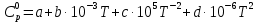
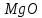
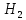
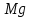
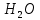
 10-3T
10-3T