Мой курсач по ОТЦ. Расчет линейных электрических цепей в переходном и стационарном режимах работы
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
Министерство связи и массовых коммуникаций Федеральное агентство связи Сибирский государственный университет телекоммуникаций и информатики Кафедра ТЭЦ КУРСОВАЯ РАБОТА по курсу ОЭ и Э Тема: расчет линейных электрических цепей в переходном и стационарном режимах работы
Новосибирск 2011 Введение Курсовая работа посвящена изучению и использованию различных методик для анализа цепей постоянного и переменного тока, а также для расчета переходных процессов в цепях постоянного тока, содержащих индуктивности и емкости. Данная курсовая работа включает в себя расчет резистивной цепи, расчет цепи с взаимно индуктивными связями при гармоническом воздействии и расчет переходных процессов второго порядка. В каждом разделе необходимо найти токи во всех ветвях схемы. Расчет токов производится различными методами. При постоянном токе это метод наложения, метод контурных токов, метод узловых напряжений и метод эквивалентного генератора (для расчета тока в одной ветви). При переменном токе - это матрично–топологический метод (контурных токов), метод эквивалентного генератора. Значение тока в каждой ветви, рассчитанное тем или иным методом, не должно быть различным. Правильность расчетов можно проверить с помощью баланса мощности. При расчете переходного процесса необходимо получить законы изменения токов во времени для каждой ветви. Техническое задание 1) Расчёт резистивной цепи 1.1 Рассчитать схему методом наложения; 1.2 Составить систему уравнений по методу законов Кирхгофа; 1.3 Рассчитать схему методом контурных токов; 1.4 Рассчитать схему методом узловых напряжений; 1.5 В резисторе 3 рассчитать ток методом эквивалентного генератора; 1.6 Проверить вычисления балансом мощности; Данные к первой части:  Рисунок 1 – исходная схема E1 = 60 В E2 = 100 В J = 10 мA R1 = 2 кOм R2 = 1 кОм R3 = 4 кОм R4 = 2 кОм R5 = 6 кОм 2) Расчёт цепи с индуктивно-связанными катушками 2.1 Матрично-топологическим методом (контурных токов) рассчитать токи во всех ветвях схемы; 2.2 Проверить расчет с помощью баланса мощности; 2.3 В конденсаторе, включенном в ветвь, не содержащую связанную катушку, рассчитать ток методом эквивалентного генератора. Данные ко второй части:  Рисунок 2 – исходная схема E1 = 20 В; E2 = j30 В; J = 10 мA; R1 = 2 кOм; R2 = 3 кОм; хL1 = 2 кОм; xL2 = 3 кОм; xm = 2 кОм; xC1 = 1 кОм; xC2 = 2 кОм. 3) Переходные процессы 3.1 Рассчитать токи в ветвях схемы классическим методом; 3.2 В ветви с конденсатором рассчитать ток операторным методом; 3.3 Построить графики  . .Данные к третьей части:  Рисунок 3 – исходная схема E = 15 В; R1 = 80 Ом; R2 =50 Ом; R3 =50 Ом; L = 10 мГн; С = 2 мкФ; 1. Расчет резистивной цепи 1.1 Расчёт схемы методом наложения Данный метод основывается на принципе суперпозиции реакции линейной электрической цепи на сумму воздействий, равной сумме реакций от каждого воздействия. Чтобы найти токи в цепи методом наложения, следует посчитать частичные схемы отдельно для каждого из источников питания, заменяя притом остальные источники их эквивалентными сопротивлениями. Метод основан на расчете токов от каждого источника отдельно, а результирующие искомые токи определяются алгебраической суммой частичных токов. Кол-во частичных схем определяется числом источников энергии. Алгоритм: Расставить произвольным образом токи в схеме Составить частичные схемы, при этом число частичны схем равно числу источников энергии. В каждой частичной схеме оставляем только один источник энергии, остальные заменяем их внутренними сопротивлениями, указываем направление токов от существующего источника. Истинные значения исходных токов определяются путем алгебраической суммы частичных токов. Правило знаков : «Частичный ток будет со знаком «+» , если его направление совпадает с выбранным направлением предварительно. Со знаком «-», если не совпадает». Перерисуем нашу схему для Е1, для этого заменяем источник тока на холостой ход, а источник напряжения Е2 на короткое замыкание:  Рисунок 1.1 - Частичная схема:          Рисунок 1.2 - Частичная схема: 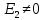  (1.18) (1.18)   Рисунок 1.3 – Частичная схема:    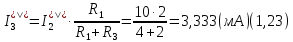  (1,24) (1,24) Найдем общие токи алгебраической суммой: 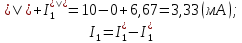     = =    = =   Искомые токи найдены без особого труда, отсюда следует вывод, что данный метод подходит для расчета сложных цепей с несколькими источниками энегии. 1.2 Система уравнений по методу законов Кирхгофа Метод законов Кирхгофа базируется на 1-ом и 2-ом законах Кирхгофа (ЗТК и ЗНК). Количество уравнений соответственно:  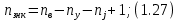 где  – число узлов в схеме – число узлов в схеме – количество ветвей в схеме – количество ветвей в схеме – количество ветвей с источником тока – количество ветвей с источником токаРасставляем произвольно направления токов в схеме Определяем количество ветвей и количество узлов, а также количество ветвей с источником тока и определяем количество уравнений:  ; ; ; ;Составляем уравнения по ЗТК:   Составляем уравнения по ЗНК: 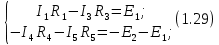  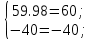 При подстановке в уравнения, составленных по законам Кирхгофа, полученных методом наложения токов, получаем верное равенство. 1.3 Метод контурных токов Обозначим контуры:  Рисунок 1.4 – Схема для расчета методом контурных токов Метод контурных токов основан на втором законе Кирхгофа. Данный метод позволяет рассчитать схему без преобразований. Алгоритм расчета: 1) Расставляем произвольным образом направление токов в схеме. 2) Определяем количество независимых контуров, задаем направление контурных токов. 3) Определяем собственные и взаимные сопротивления каждого контура, а так же собственные ЭДС каждого контура. 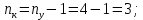 (1.30) (1.30)    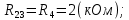 (1.35) (1.35)  4) Составляем уравнения по МКТ:  5) Решив систему уравнений, найдем контурные токи:  (1.39) (1.39)  = 2,5 (мА); = 2,5 (мА);  6  ; ;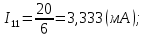  6) Определяем токи в ветвях:   10 (мА); 10 (мА);   2,5 (мА); 2,5 (мА); Так как токи совпадают с токами, рассчитанными методом наложения, то расчет верен. 1.4 Метод узловых напряжений  Рисунок 1.5– Схема для расчета методом узловых напряжений Метод без преобразования схемы. Определение узловых потенциалов по уравнениям законов токов Кирхгофа. Определение токов в ветвях по закону Ома. Алгоритм расчета: 1) Обозначаем все токи и узлы в схеме 2) Принимаем один из узлов за базисный (потенциал этого узла будет равен нулю)     3) Определяем собственные и взаимные проводимости узлов: 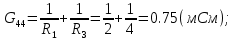    4) Составляем уравнения по МУН  5) Решив систему уравнений, найдем потенциалы узлов 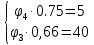   (В) (В)6) Токи в схеме найдем по закону Ома:   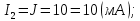 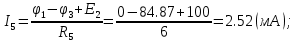   Так как токи совпадают с токами, рассчитанными методом наложения и методом контурных токов - расчет верен. 1.5 Метод эквивалентного генератора  Рисунок 1.6 – Схема для расчета по МЭГ Алгоритм расчета: 1) Обозначаем на схеме ток, который нужно найти, произвольно выбрав его направление 2) Обозначаем зажимы a и b сопротивления R, через который протекает искомый ток 3) Определяем эквивалентное сопротивление схемы относительно зажимов a и b, заменив источники на их внутреннее сопротивление:  Рисунок 1.17 - Схема для определения эквивалентного сопротивления  (1.41) (1.41)4) Определяем параметры эквивалентного источника тока: 4.1. Обозначим напряжение холостого хода , совпадающего по направлению с искомым током. 4.2. Рассчитаем полученную схему, определим Uхх Eг = Uхх., Rг = Rэкв   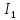 = -J = -10 (мА); (1.54) = -J = -10 (мА); (1.54) Из (1.53) найдем   = 60 – (-10) = 60 – (-10) 20 = 80 (В); 20 = 80 (В);Теперь найдем искомый ток: 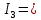  = =  (1.55) (1.55)Значение искомого тока совпало с его значениями в прошлых расчетах. 1.6 Баланс мощности Сумма мощностей, отдаваемых независимыми источниками равна сумме мощностей, потребляемых остальными элементами электрической цепи. Алгоритм расчета: 1) Определяем токи в схеме любым способом 2) Определяем мощности источников ЭДС 3) Определяем мощности источников тока (для этого нужно определить Uг) 4) Определяем мощность рассеяния на пассивных элементах схемы 5) Проверяем баланс равенство: Если  , значит токи в схеме рассчитаны верно. , значит токи в схеме рассчитаны верно. 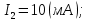   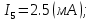 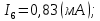         Сумма мощностей, отдаваемых независимыми источниками, равна сумме мощностей, потребляемых остальными элементами электрической цепи, значит токи в схеме рассчитаны верно. 2.1 Матрично-топологический метод В основе метода лежит представление электрической схемы с помощью графа цепи. Ветви ориентированного графа ориентированы по направлению тока ветвей. Порядок расчета: 1. Обозначить токи в ветвях произвольным образом. 2. Составить граф схемы, задать направление обхода контуров. 3. По графу составить контурную матрицу В, в которой столбцы – ветви, а строки – контуры (если направление ветви совпадает с обходом контура ставим «1», если не совпадает «-1», если ветвь не принадлежит контуру ставим «0». 4. Составляем диагональную матрицу сопротивлений ветвей Z . Диагональные элементы матрицы - сопротивления соответствующих ветвей схемы; на пересечении k – ой строки и j – го столбца, а также j – ой строки k – го столбца записывается сопротивление взаимоиндукции между индуктивно – включенными в k – ую и j – ую строки катушками индуктивности. 5. Составляем матрицу ЭДС, записывая значение источников ЭДС в соответствующую строку матрицы. 6. Составляем матрицу токов, записывая значение источников тока в соответствующую строку матрицы. 7. Составляем матрицу контурных токов. 8. Рассчитаем матрицу контурных сопротивлений. 9.Рассчитаем матрицу контурных ЭДС. 10. Получим контурные токи.  Рисунок 2.1 – Исходная схема 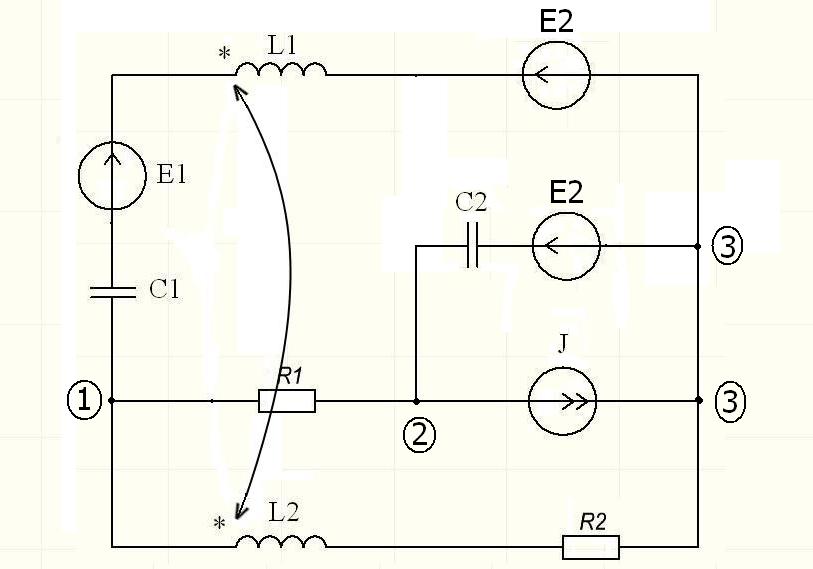 Рисунок 2.2 – Схема с развязанным источником ЭДС Уравнение электрического равновесия контурных токов: [B]  [Zв] [Zв] [Bт] [Bт] [Ik] = [B] [Ik] = [B] ([E] – [Zв] ([E] – [Zв]  ) (2.11) ) (2.11)Следует составить все матрицы, входящие в это уравнение, чтобы получить в итоге уравнения контурных токов. Составим контурную матрицу- [B], диагональную матрицу сопротивлений ветвей- [  ], матрицу ЭДС- [E], матрицу токов- [I] и матрицу контурных токов- [ ], матрицу ЭДС- [E], матрицу токов- [I] и матрицу контурных токов- [ ]; ]; 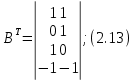    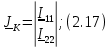 Рассчитаем матрицу контурных ЭДС:     Расчитаем матрицу контурных сопротивлений:  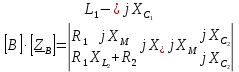 ; ; Возьмем определитель матрицы сопротивлений ветвей:  Чтобы найти контурный ток  заменим первый столбец матрицы заменим первый столбец матрицы    = 10j - 90 = 90 = 10j - 90 = 90 ; (2.25) ; (2.25) Проделаем то же самое, чтобы найти контурный ток   = -j60 = 60 = -j60 = 60 ; (2.27) ; (2.27) Зная контурные токи, найдем искомые: 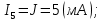     На этом расчёт цепи матрично-топологическим методом закончен. 2.2 Баланс мощности Сумма комплексных мощностей, отдаваемых независимыми источниками энергии равна сумме комплексных мощностей, потребляемых остальными элементами электрической цепи. Порядок расчета: 1. Определить токи в схеме 2. Если в схеме есть индуктивно-связанные катушки индуктивности, то нужно выполнить развязку индуктивной связи 2. Определить мощность источников ЭДС 3. Определить мощность на источниках тока 4. Определить мощность остальных элементов 5. Проверить баланс мощности:  Токи в схеме нам известны:      Выполним развязку индуктивных связей :  Рисунок 2.3 – Развязанная схема Определим мощности, отдаваемые источниками в цепь:  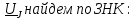  (2.21) (2.21)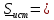 (-11.37+i3.43)(i30-20) + (13.27 – i10.67)(i30)+5(21.34 - i56.54); (-11.37+i3.43)(i30-20) + (13.27 – i10.67)(i30)+5(21.34 - i56.54); Активная мощность, рассеиваемая в резисторах схемы:   Мощность, потребляемая реактивными элементами схемы:   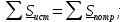 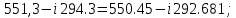 Сумма мощностей, отдаваемых независимыми источниками энергии, равна сумме мощностей потребителей, значит токи в схеме рассчитаны верно. 2.3 Метод эквивалентного генератора Метод эквивалентного генератора – метод для расчёта тока только в одной ветви электрической цепи. Ток в любой ветви линейной электрической цепи не изменяется, если активный двухполюсник к которому подключена данная ветвь заменить на эквивалентный источник напряжения с задающим напряжением равным напряжению холостого хода (ХХ) в цепи, и внутренним сопротивлением равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви. Порядок расчёта: 1. Если в схеме имеются индуктивно-связанные катушки, то следует выполнить развязку индуктивных связей 2. Обозначить на схеме ток, который нужно найти 3. Обозначить зажимы a и b, через которые протекает искомый ток 4. Определить эквивалентное сопротивление схемы относительно зажимов a и b. Источники энергии заменяются их внутреннем сопротивлением. 5. Определить параметры эквивалентного источника напряжения: 1) Обозначить между a и b напряжение  совпадающее по совпадающее понаправлению с искомым током в соответствии с рисунком 2.4 2) Рассчитать полученную схему. Определить  6. Построить эквивалентную схему и определить ток в ветви по закону Ома. Выполним развязку индуктивных связей:  Рис.2.4 – Развязанная схема  Рис.2.5 – Схема для определения      (2.26) (2.26) (2.27) (2.27)  (2.28) (2.28)Подставим известные значения в уравнение 2: 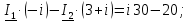 (2.29) (2.29)Выразим из второго уравнения   (2.30) (2.30)    ( ( Зная нужные токи, найдем   Теперь найдем искомый ток  : : Значение искомого тока совпало со значением, найденным матрично-топологическим методом, значит расчеты выполнены верно. 3.1 Классический метод расчета Основан на составлении интегрально – дифференциальных уравнений по законам Кирхгофа относительно независимых переменных  Интегрально – дифференциальные уравнения сводятся к одному дифференциальному уравнению n – го порядка. Интегрально – дифференциальные уравнения сводятся к одному дифференциальному уравнению n – го порядка.Порядок расчета: 1. Задать направление токов 2. Определить начальные условия а) при  б) при  3. Определить принужденную составляющую при  4. Записать характеристическое уравнение, найти его корни 5. Зная корни, записать общее решение xсв(t) 6. Для x(t)=xсв(t)+xпр(t) используя начальные условия, определить независимую постоянную интегрирования 7. Записать закон изменения x(t). 8. Построить графики Определим начальные условия:  Рисунок 3.1 – Схема для момента времени      Рисунок 3.2 – Схема для момента времени  Cохраняются начальные условия:   0,0833 (А); 0,0833 (А);  ; (3.13) ; (3.13)  (3.14) (3.14)  (3.15) (3.15) (3.16) (3.16)    Рисунок 3.3 – Схема для момента времени   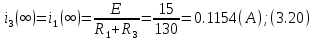 Запишем характеристическое уравнение и найдем его корни:  Рисунок 3.4 – Схема для нахождения характеристического уравнения       Так как корни комплексно-сопряженные - это колебательный процесс. Составим уравнения токов:  (3.25) (3.25) (3.26) (3.26)tg    (3.27) (3.27) (3.28) (3.28)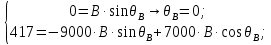 (3.29) (3.29)B = 0.0596;   (3.30) (3.30) (3.31) (3.31) (3.32) (3.32) C= - 0.0523;  (3.33) (3.33)Уравнения токов найдены, на этом расчет классическим методом закончен. 3.2 Операторный метод расчета Операторный метод основывается на преобразованиях Лапласа, которые позволяют систему дифференциальных уравнений свести к системе алгебраических уравнений. Порядок расчёта: 1. Обозначить токи в цепи 2. Определить ННУ 3. Составить операторную схему замещения 4. По данной схеме, используя любой метод расчёта записать изображение искомых величин 5. Используя обратное преобразование Лапласа найти оригинал искомой величины. Составим операторную схему замещения и решим ее по методу узловых потенциалов:  Рисунок 3.5 – Операторная схема замещения Уравнение по МУН:    Пусть          Так как полюсы комплексно-сопряженные, находим ток по формуле:  Полученный ток совпадает с током, найденным классическим методом, значит расчет верен. 3.3 Графики   Рисунок 3.6 – График   ; ; Рисунок 3.7 – График    Рисунок 3.6 – График  По построенным графикам можно наблюдать характер тока и его изменения ва времени. Найденные значения токов в определенные моменты времени, а именно моменты до, во время и после коммутации, соответствуют значениям, определенным по графикам в эти же моменты времени. Заключение Для расчета резистивной цепи применялись методы контурных токов, наложения, узловых потенциалов и метод эквивалентного генератора. Найденные токи в ветвях оказались верными, так как значения токов, полученные разными методами, оказались одинаковыми. И также правильность вычислений была проверена с помощью баланса мощности. Расчет цепи с взаимно-индуктивными связями включал в себя матрично-топологический метод и метод эквивалентного генератора. И также вычисления оказались верными. Расчет переходного процесса был произведен классическим и операторным методами. На основании полученных уравнений токов были построены графики зависимости тока от времени. Поставленные в курсовом проекте цели и задачи полностью выполнены. Список литературы 1.Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники – М.: Радио и связь, 1989. – 528 с. 2. Тихобаев В.Г. Расчет линейных электрических цепей в переходном и стационарном режиме. Методические указания к курсовой работе. СибГУТИ, 2003. 3. Бакалов В.П., Журавлева О.Б., Крук Б.И. Основы анализа цепей – М.: Горячая Линия – Телеком, 2007. |
