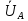ТОЭ. Электротехника. Расчет линейных электрических цепей
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА федеральное государственное бюджетное образовательное учреждение высшего образования «ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» (ОмГУПС (ОмИИТ)) Кафедра: «Теоретическая электротехника» РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Пояснительная записка к курсовой работе по дисциплине «Теоретические основы электротехники» ИНМВ. 400089. 000 ПЗ Студент гр. СП-80189 ______М.М. Садреев Дата Руководитель – к. т. н., доценткафедры ТЭ _______ Дата Омск 2021 Реферат УДК 621.3 Курсовая работа содержит 21 страницу, 12 рисунков, 2 таблицы, 2 источника. Линейная электрическая схема, расчетная схема замещения, несинусоидальные токи и напряжения, ряд Фурье, однофазные и трехфазные цепи, несимметрия трехфазной цепи, переходные процессы, временные и векторные диаграммы. Объектом исследования являются однофазные и трехфазные линейные электрические цепи. Цель работы – расчет однофазной цепи при несинусоидальном питающем напряжении, симметричной и несимметричной трехфазной цепи при синусоидальных питающих напряжениях, разветвленной цепи с одним и двумя накопителями энергии при воздействии постоянных источников ЭДС во время переходного процесса. Методы исследования – аналитические и графические. Произведен расчет разветвленной цепи, получающей питание от источника несинусоидального напряжения, при помощи метода наложения. Построены заданная кривая напряжения на входе цепи и расчетная кривая тока. Рассчитаны симметричная и несимметричная трехфазные цепи при синусоидальном питающем напряжении, составлен баланс мощностей, построены векторные топографические диаграммы, определены показания ваттметров, включенных в цепь. Рассчитана симметричная трехфазные цепи при несинусоидальном питающем напряжении. Произведен расчет напряжения на конденсаторе при переходном процессе для цепи с двумя накопителями энергии при питании ее от источника постоянного напряжения (тока), построены графики рассчитанной функции. Рассчитаны независимые начальные условия переходного процесса на переменном токе. Произведен расчет цепи с одним накопителем энергии операторным методом. Содержание
Введение Электротехника – это наука о техническом применении электрических и электромагнитных явлений в практических целях. Почти все области деятельности современного общества развиваются на базе широкого применения электротехнических устройств. Электротехническим устройством называют промышленное изделие, предназначенное для определенной функции: получения, преобразования, передачи и распределения электрической энергии. Электротехническое устройство может содержать электрические и магнитные цепи. Электрической цепью называют совокупность элементов, предназначенных для протекания электрического тока. Анализ режимов работы цепей заключается в расчете основных электрических величин: тока, напряжения и мощности при известных значениях параметров элементов электрической цепи. Величина тока является определяющей в расчетах электрической цепи, поэтому анализ режимов работы цепей часто сводится к отысканию значений тока в ветвях. Существуют различные методы расчета цепей, эффективность применения которых зависит от свойств электрической цепи. Расчет одно- и трехфазных цепей переменного тока рассматривается с применением аппарата комплексных чисел. Правильность анализа электрических цепей оценивается с помощью составления баланса мощности, в соответствии с которым сумма значений мощности, отдаваемой источниками, равна сумме значений мощности, потребляемой приемниками. Если значения этих мощностей равны, значит, расчеты выполнены верно. Для проверки правильности расчетов в цепях переменного тока также используются векторные диаграммы, которые строятся по результатам расчетов и должны отражать реальное распределение энергетических параметров и выполнение законов электротехники, важнейшими из которых являются закон Ома и законы Кирхгофа. Переходные процессы сопровождают переход электрической цепи или системы из одного установившегося состояния в другое и возникают при любых изменениях параметров электрических цепей. Мгновенные изменения параметров называют коммутациями. Наиболее распространенными коммутациями являются включения или выключения электрических цепей в целом или отдельных их участков. Переходные процессы в исключительном большинстве случаев длятся какое-то время. Объясняется это тем, что любая электрическая цепь запасает энергию электромагнитного поля. При этом энергия магнитного поля сосредоточивается в индуктивностях, а электрического – в емкостях. Электромагнитная энергия не может быть изменена мгновенно, т.е. нельзя ее мгновенно накопить, или, наоборот, израсходовать. Это обстоятельство и определяет длительность протекания во времени любых переходных процессов. В зависимости от количества активных и реактивных элементов, а также от структуры электрической цепи изменения токов и напряжений в переходных процессах могут быть достаточно сложными. В реальных условиях переходные процессы могут сопровождаться возникновением электрической дуги. В основном это случаи размыкания электрических ветвей с индуктивностями, накапливающими энергию магнитного поля. Такие случаи при изучении основ математического исследования переходных процессов в линейных электрических цепях не рассматриваются. Поэтому при изучении методов расчета переходных процессов будут отсутствовать такие коммутации, например, как размыкание ветвей с индуктивностями. К коммутациям, используемым во всех приведенных примерах и задачах, применимо допущение об отсутствии электрической дуги. 1 Расчет линейной электрической цепи при несинусоидальном входном напряжении 1) Разложить заданное напряжение в ряд Фурье, ограничившись пятью гармониками (включая нулевую). 2) Построить в одной системе координат временные графики гармоник напряжения, суммарную кривую и заданное напряжение. Определить: 1) действующее значение напряжения U; 2) входное сопротивление и мгновенное значение тока для всех гармоник напряжения; 3) мгновенное значение тока на неразветвленном участке i и действующее значение тока I; 4) активную P, реактивную Q и полную S мощности цепи; 5) форму кривой тока i, для чего на чертеже построить токи гармоник и суммарную кривую тока i, полученную в результате графического сложения отдельных гармоник. К цепи (рисунок 1.1) приложено напряжение u (рисунок 1.2), описываемое выражением: 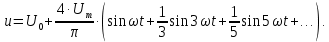  Рисунок 1.1 – Расчетная схема  Рисунок 1.2 – Форма входного напряжения Таблица 1.1 – Исходные данные
В расчете учтем первую, третью, пятую гармоники. Решение Действующее значение приложенного напряжения 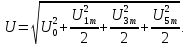 Рассчитанные амплитуды гармоник напряжения (нулевая соответствует постоянному току): 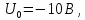 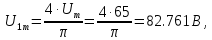 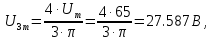 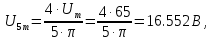 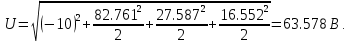 Таким образом, приложенное напряжение 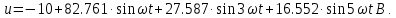 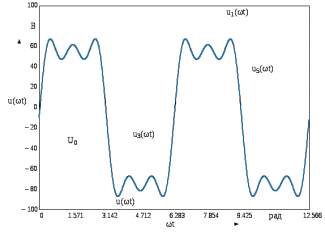 Рисунок 1.3 – График входного напряжения Входное сопротивление цепи на постоянном токе: 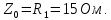 Входное сопротивление цепи на переменном токе – для тока гармоник: 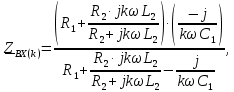 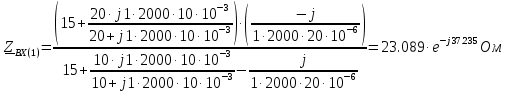 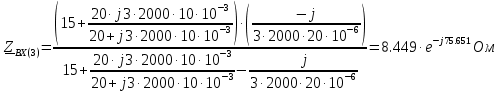 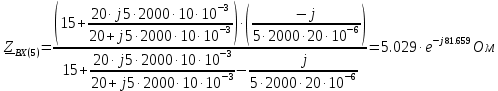 Рассчитаем входной ток цепи на гармониках входного напряжения: 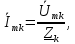 где Umk– амплитуда напряжения k-ой гармоники, Zk – входное сопротивления цепи на частоте k-ой гармоники. 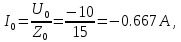 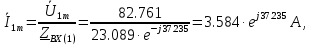 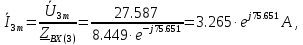 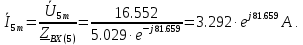 Ток на неразветвленном участке цепи 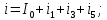 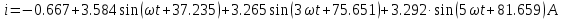 Действующее значение тока на неразветвленном участке цепи 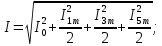 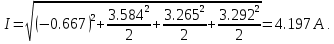 Активная мощность цепи 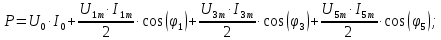 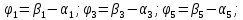 где 1, 3, 5 – начальные фазы гармоник напряжения; 1, 3, 5 – начальные фазы гармоник тока. 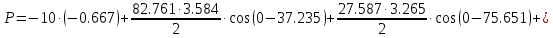 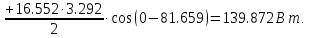 Реактивная мощность цепи 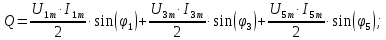 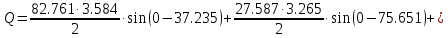 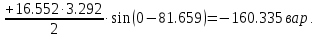 Полная мощность цепи 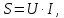 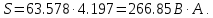 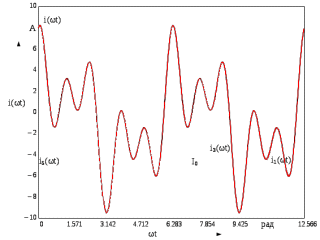 Рисунок 1.4 – Кривая входного тока 2 Расчёт симметричной трёхфазной цепи Найти токи в линии и в фазах нагрузки, показания ваттметров, составить баланс мощностей, построить векторную диаграмму токов и напряжений. 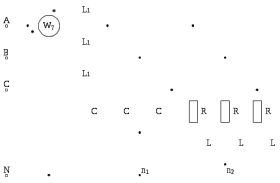 Рисунок 2.1 – Схема трехфазной электрической цепи Таблица 2.1 – Параметры элементов цепи и значение приложенного напряжения
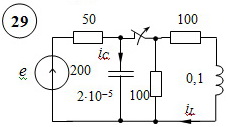
Решение. Расчет симметричной трехфазной электрической цепи, приведенной на рисунке 2.1, целесообразно выполнять на одну фазу. Расчетная схема замещения относительно фазы А приведена на рисунке 2.2.  Рисунок 2.2 – Расчетная схема замещения Рассчитаем линейное напряжение 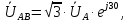 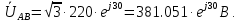 Рассчитаем эквивалентное сопротивление замещенной цепи. 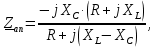 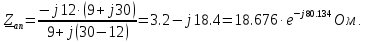 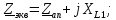 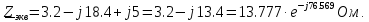 Рассчитаем линейные и фазные токи: 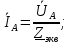 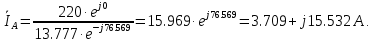 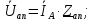 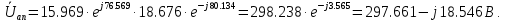 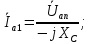 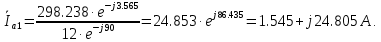 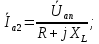 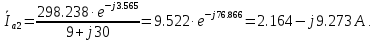 Составим баланс мощностей. Активная мощность цепи равна суммарной мощности потерь в резисторах: 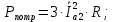 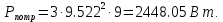 Реактивная мощность цепи: 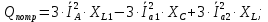 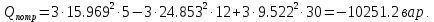 Комплексная мощность источника: 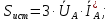 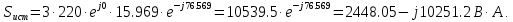 Показание ваттметра: 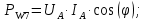 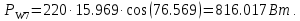 mI = 4 A/см mU = 44 В/см  Рисунок 2.3 – Векторная диаграмма токов и напряжений трехфазной электрической цепи 3 Расчёт несимметричной трёхфазной цепи Задача расчета токов и напряжений в трехфазной электрической цепи усложняется, если хотя бы в одном ее месте нарушено условие симметрии: несимметрична трехфазная система ЭДС или источников тока, различны параметры соответствующих элементов фаз. В таких случаях всю трехфазную цепь рассматривают как разветвленную цепь с несколькими однофазными источниками [1].  Рисунок 3.1 – Данная схема Параметры элементов цепи: 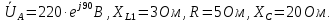 Найти токи в ветвях, составить баланс мощностей, построить векторную диаграмму токов и напряжений. 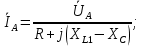 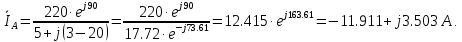 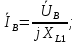 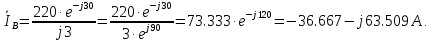 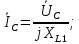 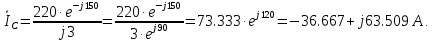 По первому закону Кирхгофа: 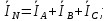 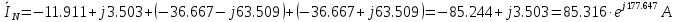 Составим баланс мощностей. Комплексная мощность источника: 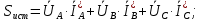 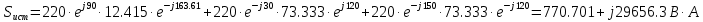 Активная мощность цепи равна суммарной мощности потерь в резисторах: 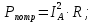 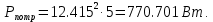 Реактивная мощность цепи: 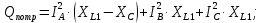 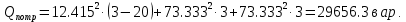 mI = 10 A/см mU = 50 В/см  Рисунок 3.2 – Векторная диаграмма токов и напряжений трехфазной электрической цепи 4 Расчет переходного процесса в цепи с одним накопителем энергии В цепи, с одним накопителями энергии (рисунок 4.1) при наличии источника постоянной ЭДС (тока) определить любой ток или напряжение операторным методом.
До размыкания (t = 0-) имеет место установившийся режим постоянных токов. Эквивалентное входное сопротивление 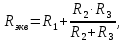 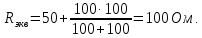 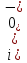 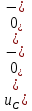 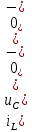 Согласно первому закону коммутации, определяющему непрерывность тока в индуктивности: 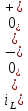 Составим дифференциальное уравнение для послекоммутационного состояния. Используя формулы соответствия оригиналов и изображений, составим алгебраическое уравнение для изображений: 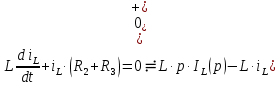 решение которого – 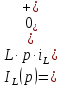 Получили изображение тока в катушке индуктивности в виде 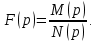 Определим корни знаменателя, решив уравнение N(p) = 0: 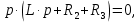 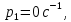 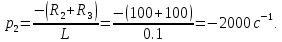 Производная знаменателя: 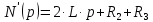 Переходя от изображения к оригиналу, получаем [2]: 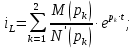 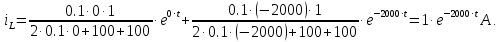 5 Расчет переходного процесса в цепи с двумя накопителями энергии В цепи с двумя накопителями энергии в переходном режиме классическим методом определить закон изменения напряжения на ёмкости uС, если в цепи действует источник постоянного напряжения (тока). Построить график изменения рассчитанной функции. При питании от источника синусоидального напряжения (тока) определить независимые начальные условия переходного процесса.
1. До замыкания (t = 0-). Имеет место установившийся режим постоянных токов. Эквивалентное сопротивление цепи: 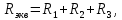 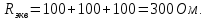 По закону Ома  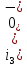 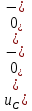 2. Дифференциальные уравнения описывают токи и напряжения с момента t = 0+ По второму закону Кирхгофа запишем систему уравнений: 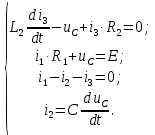 3. Принужденный режим. Принужденные составляющие находятся из рассмотрения установившегося режима, наступающего после переходного процесса. 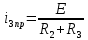 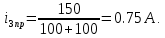 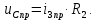 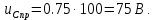 4. Свободный режим. Составляем характеристическое уравнение 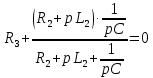 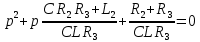 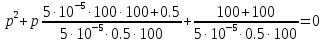 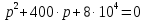 Данное характеристическое уравнение имеет корни 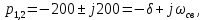 где δ = 1000 – коэффициент затухания, ωсв = 1000 с-1 – угловая частота свободных колебаний. Следовательно, имеет место колебательный режим переходного процесса. 5. Общее решение 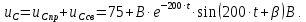 6. Определение зависимых начальных условий Согласно первому закону коммутации, определяющему непрерывность тока в индуктивности: 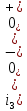 Согласно второму закону коммутации напряжение на емкости в моменты коммутации не может изменяться мгновенно, или скачком: 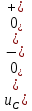 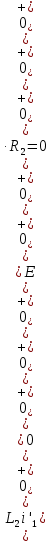 Откуда 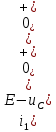 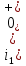 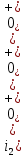 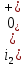   7. Определение коэффициентов Составляем систему уравнений 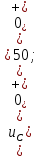 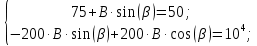 Откуда 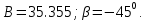 Таким образом, закон изменения напряжения на ёмкости 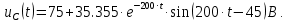 График изменения рассчитанной функции представлен на рисунке 5.2. 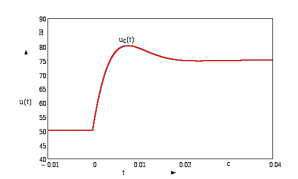 Рисунок 5.2 – График зависимости uC(t)8. Определим независимые начальные условия при питании от источника синусоидального напряжения (тока) До замыкания (t = 0-). Имеет место установившийся режим синусоидальных токов. Расчет проводим комплексным методом. Комплексная амплитуда тока 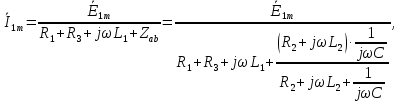 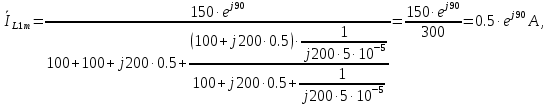 Мгновенное значение тока 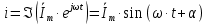 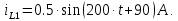 В момент замыкания  Комплексная амплитуда напряжения 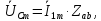 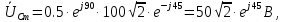 Мгновенное значение напряжения 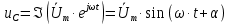 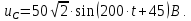 В момент замыкания 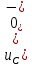 Комплексная амплитуда тока 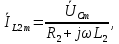 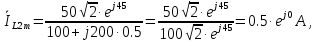 Мгновенное значение тока 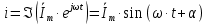 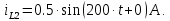 В момент замыкания 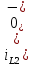 Заключение В ходе курсовой работы были исследованы работы однофазной цепи при несинусоидальном питающем напряжении, симметричной и несимметричной трехфазной цепи при синусоидальных питающих напряжениях, разветвленной цепи с одним и двумя накопителями энергии при воздействии постоянных источников ЭДС и тока во время переходного процесса. При этом использовались – аналитические и графические методы исследования. Произведен расчет цепи при воздействии на нее несинусоидального источника напряжения. Построен график тока в цепи, полученный в результате графического сложения отдельных гармоник. Рассчитаны симметричная и несимметричная трехфазные цепи. Составлен баланс мощностей, построены векторные диаграммы напряжений и токов. Исследованы линейные цепи с одним и двумя накопителями энергии в переходных режимах работы, построен график функций напряжения на емкости от времени. Библиографический список 1. Тэттэр А. Ю. Периодические режимы однофазных и трехфазных электрических цепей: Учебное пособие / А.Ю. Тэттэр, В.Т. Черемисин, Т.В. Ковалева и др. / Омский гос. ун-т путей сообщения. Омск, 2013. 132 с. 2. Кузнецов А.А. Переходные процессы в линейных электрических цепях: Учебное пособие / А.А. Кузнецов, А.В. Пономарев, А.Ю. Тэттэр / Омский гос. ун-т путей сообщения. Омск, 2013. 102 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||