сапромат. Расчет на изгиб двутавровой балки
 Скачать 285.83 Kb. Скачать 285.83 Kb.
|
|
РАСЧЕТ НА ИЗГИБ ДВУТАВРОВОЙ БАЛКИ Условия задачи Двутавровая стальная балка закреплена на двух шарнирных опорах и нагружена в соответствии с заданной расчетной схемой (рис. 1). Допускаемые напряжения  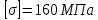 , модуль упругости , модуль упругости 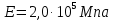 . . Требуется: Записать выражения и построить эпюры для изгибающих моментов и перерезывающих сил по силовым участкам; Из условия полной проверки на статическую прочность подобрать по ГОСТу требуемый номер двутаврового профиля; С использованием универсального уравнения упругой линии записать выражения для прогибов и углов поворота по силовым участкам; Построить эпюры углов поворота (в градусах) и прогибов (в миллиметрах). 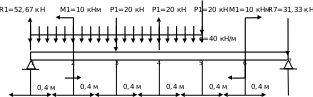 Рис. 1.1. Расчетная схема двутавровой балки Исходные данные Таблица 1.1.
Определение перерезывающих сил и изгибающих моментов Выбираем систему координат (начало системы координат совмещено с левым концом балки) и разбиваем балку на силовые участки. Границы силовых участков обозначены цифрами 1,2,3,4,5,6,7. Используя исходные данные, представим заданные усилия в безразмерном виде: 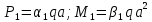 , ,где 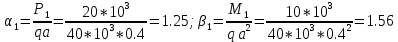 Определяем реакции опор: 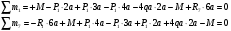 (1.1) (1.1)Из (1.1) находим: 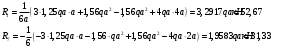 Проверка: 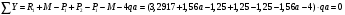 Найденные значения для 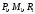 и и 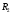 подписываем на расчетной схеме (рис. 1.1). подписываем на расчетной схеме (рис. 1.1).Последовательное рассматриваем силовые участки и записываем уравнения для Q и M. Участок 1-2 ( 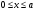 ) )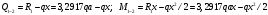 Характерные значения: 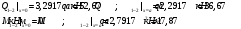 Участок 2-3 ( 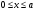 ) )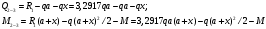 Характерные значения: 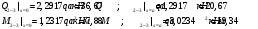 Участок 3-4 ( 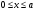 ) )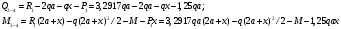 Характерные значения: 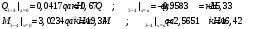 Так как 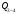 на границах силового участка имеет разные знаки, в точке на границах силового участка имеет разные знаки, в точке 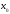 такой, что такой, что 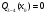 , эпюра , эпюра 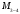 будет иметь экстремум. будет иметь экстремум.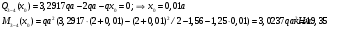 Участок 4-5 ( 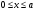 ) )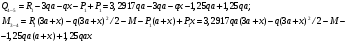 Характерные значения: 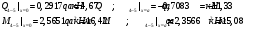 Так как 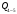 на границах силового участка имеет разные знаки, в точке на границах силового участка имеет разные знаки, в точке 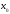 такой, что такой, что 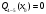 , эпюра , эпюра 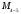 будет иметь экстремум. будет иметь экстремум.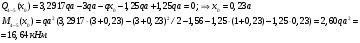 Участок 5-6 ( 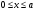 ) )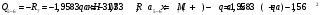 Характерные значения: 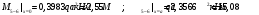 Участок 6-7 ( 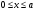 ) )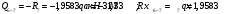 Характерные значения: 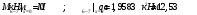 Эти выражения могут быть получены по методу сечений, если при составлении уравнений отбросить левую часть балки. Используя полученные результаты, строим эпюры Q и M (рис. 1.2).  Рис. 1.2. Эпюры Q и M Расчет балки на полную статическую прочность при изгибе Номер двутаврового сечения балки определяем из расчета на прочность по максимальным нормальным напряжениям. В сечении с 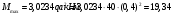 Должно выполняться условие  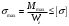 , откуда находим потребный момент сопротивления балки , откуда находим потребный момент сопротивления балки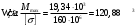 По ГОСТу выбираем ближайший по моменту сопротивления профиль № 18 с 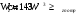 . Схематическое изображение сечения представлено на рис. 1.3. . Схематическое изображение сечения представлено на рис. 1.3.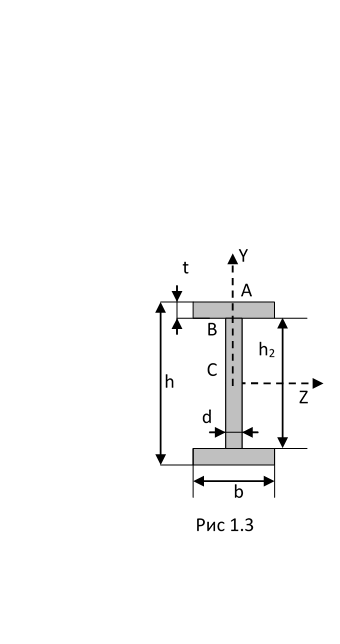 Рис. 1.3. Сечение балки Геометрические и жесткостные параметры двутаврового профиля: 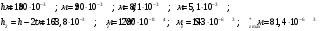 Выполняем проверку по максимальным касательным напряжениям. В сечении с максимальным значением перерезывающей силы проверяем прочность в точке С поперечного сечения балки 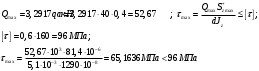 Прочность по максимальным касательным напряжениям обеспечена. Проверяем прочность (по четвертой теории прочности) точки B поперечного сечения балки (рис 1.3), которая соответствует максимальному значению эквивалентного напряжения. Это будет фиктивное сечение. 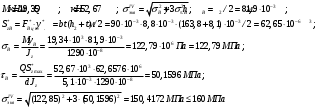 Выбранный двутавр № 18 удовлетворяет условиям прочности. Определение прогибов и углов поворота балки Для определения прогибов и углов поворота воспользуемся универсальными уравнениями упругой линии балки с постоянной жесткостью, которое в данном случае имеет вид: 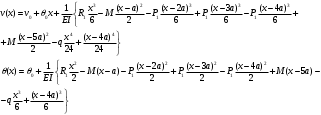 (1.2) (1.2)Где 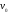 и и 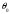 - произвольные постоянные. - произвольные постоянные.В (1.2) следует учитывать силовые факторы, лежащие слева от рассматриваемого сечения, так что выражения в круглых скобках всегда больше или равны нулю. Произвольные постоянные 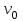 и и 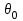 определяются из граничных условий: определяются из граничных условий: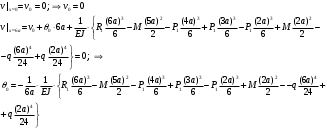 Вычисления по формулам (1.2) удобно проводить с помощью ЭВМ. С помощью программы составленной на языке Фортран, приведенной в приложении 1, строим эпюры, представленные на рисунке 1.4.  Рис. 1.4. Эпюры Q, M, θ, v |
