Расчет периодических процессов в нелинейных цепях
 Скачать 68.2 Kb. Скачать 68.2 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова» Высшая школа энергетики, нефти и газа (наименование высшей школы / филиала / института / колледжа) КОНТРОЛЬНАЯ РАБОТА
Архангельск 2022 ЗаданиеВариант 8, схема В, m=8, n=16, w = 100m/2 = 400; r = 1,5 (m+n) = 36 Ом; xL = 5 (m+n/2) = 80 Ом; xC = 7,5 (m+n/3) = 100 Ом. Рассчитать режим нелинейной электрической цепи, содержащей катушку с ферромагнитным сердечником. Закон изменения магнитной индукции внутри сердечника известен 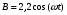 Тл. Схема цепи, размеры сердечника и частота магнитной индукции заданы табл. 16.3 в сборнике заданий. Найти токи и напряжения на всех элементах цепи и определить показания приборов. Схема и параметры цепи задаются буквенной литерой, цифрами m и n. Тл. Схема цепи, размеры сердечника и частота магнитной индукции заданы табл. 16.3 в сборнике заданий. Найти токи и напряжения на всех элементах цепи и определить показания приборов. Схема и параметры цепи задаются буквенной литерой, цифрами m и n.Таблица 1 Кривая намагничивания электротехнической стали магнитопровода
Аппроксимировать нелинейную зависимость 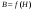 рекомендуется полином следующего вида: H = a1 B + a2 B3. В качестве критерия точности аппроксимации необходимо обеспечить условие: максимальное отклонение не должно превышать 0,20 Тл в пределах пологого (приблизительно в интервале 400 3000 А/м2) участка характеристики. Кривую, соответствующую аналитическому выражению построить на одном графике с кривой, соответствующей конкретному варианту (числу m). Сравнить их для проверки выполнения заданного критерия. Рассеянием и потерями в сердечнике пренебречь. рекомендуется полином следующего вида: H = a1 B + a2 B3. В качестве критерия точности аппроксимации необходимо обеспечить условие: максимальное отклонение не должно превышать 0,20 Тл в пределах пологого (приблизительно в интервале 400 3000 А/м2) участка характеристики. Кривую, соответствующую аналитическому выражению построить на одном графике с кривой, соответствующей конкретному варианту (числу m). Сравнить их для проверки выполнения заданного критерия. Рассеянием и потерями в сердечнике пренебречь.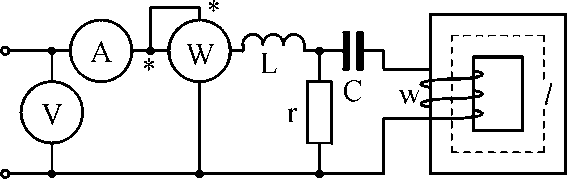 Рисунок 1 - Расчетная схема Лист для замечанийРАСЧЁТ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЦЕПЯХВыполним расчет схемы, представленной на рисунке 1. Данная схема содержит нелинейный элемент – катушку со стальным сердечником. Характеристика катушки 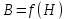 задана графиком на рисунке 3 (кривая 1). Известно, что магнитная индукция в сердечнике изменяется по закону задана графиком на рисунке 3 (кривая 1). Известно, что магнитная индукция в сердечнике изменяется по закону 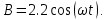 Число витков катушки w=400, средняя длина магнитопровода l=0,5 м, площадь поперечного сечения Число витков катушки w=400, средняя длина магнитопровода l=0,5 м, площадь поперечного сечения 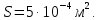 Сопротивление линейных элементов в комплексной форме: r=36 Ом, XL=j80 Ом, XC=-j100. Циклическая частота Сопротивление линейных элементов в комплексной форме: r=36 Ом, XL=j80 Ом, XC=-j100. Циклическая частота 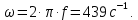
Рисунок 2 – Табличная форма характеристики катушки Найдем аналитическое выражение для характеристики катушки, кривой намагничивания 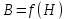 (кривая 1 (пунктир)). В качестве аппроксимирующей функции возьмем полином вида (кривая 1 (пунктир)). В качестве аппроксимирующей функции возьмем полином вида 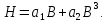 Выберем на кривой 1 две точки. Выберем на кривой 1 две точки.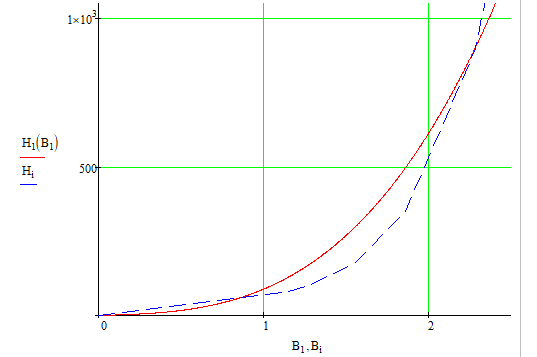 Рисунок 3 - График характеристики катушки и аппроксимирующей функции Это точки с координатами B1=0,86 Тл, H1=60 А/м, и B2=2,28 Тл, H2=900 А/м. Подставив в аппроксимирующий полином, получим следующую систему: 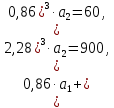 решение данной системы определяет коэффициенты полинома. 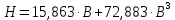 . Из графика на рисунке 2 (кривая 2) видно, что такой полином достаточно точно отображает заданную нелинейную зависимость. Пользуясь этим результатом, найдем ток, протекающий по обмотке катушки. Закон полного тока в записи для магнитной цепи, . Из графика на рисунке 2 (кривая 2) видно, что такой полином достаточно точно отображает заданную нелинейную зависимость. Пользуясь этим результатом, найдем ток, протекающий по обмотке катушки. Закон полного тока в записи для магнитной цепи,  позволяет выразить ток: позволяет выразить ток: (1) (1)Заменим данную косинусоиду эквивалентной синусоидой.  . .Рассчитаем ток катушки по формуле (1): 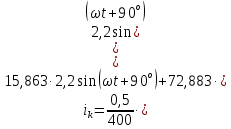 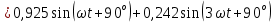 . .Запишем ток на катушке в комплексной форме, в действующем значении: 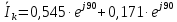 А АРассчитаем напряжение на катушке по следующей формуле: 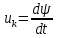 (2) (2)где потокосцепление 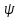 равняется: равняется: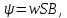 (3) (3)Подставим формулу (3) в (2) и получим следующее выражение: 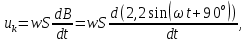 (4) (4)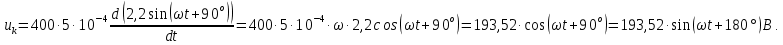 Запишем напряжение катушки в комплексной форме в действующем значении: 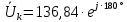 В. В.После определения, составляющих катушки найдем токи и напряжения на линейных элементах. При расчёте отдельных гармонических режимов будем использовать комплексный метод расчёта. Рассчитаем напряжение на емкости, ток на катушке равен току на емкости, расчёт будем вести в действующих значениях: Для первой гармоники: 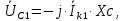 (5) (5)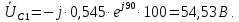 Для третьей гармоники: 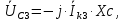 (6) (6)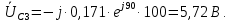 Запишем напряжение на емкостном сопротивлении в мгновенных значениях: 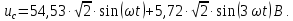 Рассчитаем напряжение на резисторе. Оно равно сумме напряжений на емкости и катушке: Для первой гармоники: 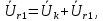 (7) (7)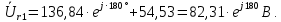 Поскольку в напряжении катушки третья гармоника отсутствует, третья гармоника на резисторе равна третьей гармонике на емкости: 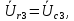 (8) (8)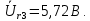 Запишем напряжение на резисторе в мгновенных значениях:  Рассчитаем ток на резисторе: Для первой гармоники: 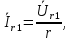 (9) (9)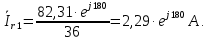 Для третьей гармоники: 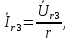 (10) (10)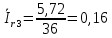 А. А.Запишем ток на резисторе в мгновенных значениях: 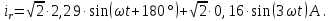 Ток через индуктивность равен общему току цепи, то есть: 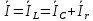 , (11) , (11)При этом следует помнить, что ток на катушке равен току на емкости. Для первой гармоники: 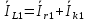 , (12) , (12)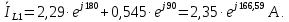 Для третьей гармоники: 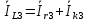 , (13) , (13)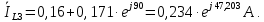 Тогда полный ток и соответственно ток индуктивности в мгновенных значениях равен: 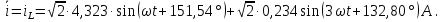 Рассчитаем напряжение на индуктивности: Для первой гармоники: 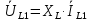 , (14) , (14)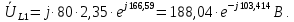 Для третьей гармоники: 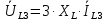 , (15) , (15)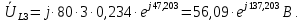 Запишем напряжение на индуктивности в мгновенном значении: 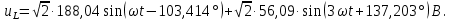 Рассчитаем полное напряжение, приложенное к цепи: 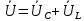 , (16) , (16)Для первой гармоники: 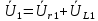 , (17) , (17)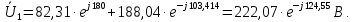 Для третьей гармоники:  , (18) , (18)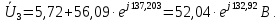 Запишем полное напряжение, приложенное к цепи, в мгновенном значении: 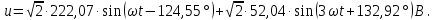 Определим показания приборов. Показания амперметра и вольтметра есть действующие значения несинусоидальных периодических тока и напряжения на входе цепи. Где ток равен: 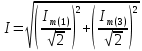 , (19) , (19)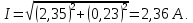 Где напряжение равно:  , (20) , (20) Показание ваттметра есть активная мощность всей цепи, равна мощности активных мощностей каждой гармоники по отдельности: 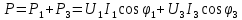 , (21) , (21)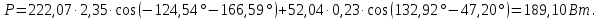 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
