Расчетная работа по логистике. Расчет разгрузочных маршрутов с баз и складов снабжения и сбыта для перевозки мелкопартионных грузов потребителям
 Скачать 45.81 Kb. Скачать 45.81 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ» (КНИТУ-КАИ) Чистопольский филиал «Восток» кафедра экономики и управления 38.03.01 Экономика РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА по дисциплине «Логистика» На тему: «Расчет разгрузочных маршрутов с баз и складов снабжения и сбыта для перевозки мелкопартионных грузов потребителям» Выполнил: обучающийся гр. 21403 ________Калмыкова Ю.А. подпись Проверил: доцент ______________Мунина М.В. подпись Чистополь, 2019 г. 1. Расчет задания расчетно-графической работы Заданы пункты потребления Xi, (i = 1, 2, ..., n). Груз необходимо развезти из начального пункта Хо(склад) во все остальные Xi (потребители). Таблица 1 Потребители продукции и объемы завоза
Известно также расстояние перевозки  между потребителями. Грузоподъемность автомобиля 2,5 т. между потребителями. Грузоподъемность автомобиля 2,5 т.Схема размещения пунктов и расстояния между ними приведены на рис. 1.   Рис. 1. Схема размещения пунктов и расстояния между ними Решение Этап I. Строим кратчайшую сеть, связывающую все пункты без замкнутых контуров («минимальное дерево» рис. 2). Г А  Ж  Д  И К Е  З  В Б Рис. 2 Кратчайшая связывающая сеть («минимальное дерево») Затем по каждой ветви сети, начиная с пункта, наиболее удаленного от начального пункта 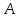 (считая по кратчайшей связывающей сети), группируем пункты на маршрут с учетом количества ввозимого груза и грузоподъемности единицы подвижного состава. Ближайшие к другой ветви пункты группируем вместе с пунктами данной ветви. Исходя из данной грузоподъемности подвижного состава, сгруппируем маршруты в таблице 2. (считая по кратчайшей связывающей сети), группируем пункты на маршрут с учетом количества ввозимого груза и грузоподъемности единицы подвижного состава. Ближайшие к другой ветви пункты группируем вместе с пунктами данной ветви. Исходя из данной грузоподъемности подвижного состава, сгруппируем маршруты в таблице 2.Таблица 2 Группировка маршрутов исходя из грузоподъемности автомобиля
Сгруппировав пункты по маршрутам, переходим к этапу II расчетов. Этап II. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу (табл. 3), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках — кратчайшие расстояния между ними. Таблица 3 Матрица для определения рационального порядка объезда пунктов
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке (40,4;40;27,2), т.е. 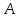 ; ; ;Ж. Для включения последующих пунктов выбираем из оставшихся пункт, имеющий небольшую сумму, например, пункт ;Ж. Для включения последующих пунктов выбираем из оставшихся пункт, имеющий небольшую сумму, например, пункт 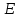 (сумма 26,4) и решаем, между какими пунктами его следует включать, т.е. между (сумма 26,4) и решаем, между какими пунктами его следует включать, т.е. между 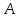 и и  , ,  и Ж или и Ж или 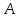 и Ж. и Ж.Чтобы это решить, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле 1: 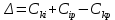 (1) (1)где 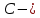 расстояние, км.; расстояние, км.;  индекс включаемого пункта; индекс включаемого пункта;  индекс первого пункта из пары; индекс первого пункта из пары;  индекс второго пункта из пары. индекс второго пункта из пары.При включении пункта 7 между первой парой пунктов А и К определяем размер приращения ΔАК при условии, что i = 7; к = А; р = К. Тогда  (2) (2)Подставляем значения из табл. 3. Получаем, что 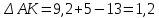 км. Таким же образом определяем приращение км. Таким же образом определяем приращение 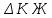 (если пункт 3 включить между пунктами (если пункт 3 включить между пунктами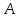 и Ж), км.: и Ж), км.: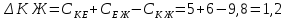 км.; км.;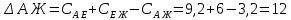 км. км.Из полученных значений выбираем минимальное, т.е.  км. км.Следовательно, пункт 7 должен быть между пунктами 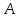 и и . Получаем маршрут вида: . Получаем маршрут вида: 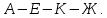 Используя этот метод и формулу приращения, определяем, между какими пунктами расположить пункты Д и И. Начнем с И, так как размер суммы (табл. 3) этого пункта больше (23,6 > 22,4). Итак, км.: 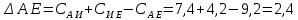 км.; км.; км.; км.; км. км.В том случае, когда Δ = 0, для симметричной матрицы расчеты можно не продолжать, так как значение меньшее, чем 0, получено быть не может. Поэтому пункт И должен быть между пунктами 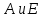 (т.к. (т.к.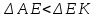 ). Тогда маршрут будет иметь вид: ). Тогда маршрут будет иметь вид: 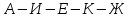 . .В результате проведенного расчета включаем следующий пункт Д между пунктами 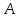 и И, так как для этих пунктов получено минимальное приращение 2 км.: и И, так как для этих пунктов получено минимальное приращение 2 км.: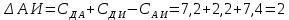 км.; км.;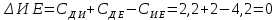 км. км.Таким образом, окончательный порядок движения по маршруту I будет:  , длиной 28,4 км. , длиной 28,4 км.Таким же методом определяем кратчайший путь объезда пунктов по маршруту II. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу (табл. 4), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках — кратчайшие расстояния между ними. Таблица 4 Матрица для определения рационального порядка объезда пунктов
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке (25,7;23,7;22,8), т.е 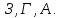 Для включения последующих пунктов выбираем из оставшихся пункт, имеющий небольшую сумму, например, пункт  (сумма 21,2) и решаем, между какими пунктами его следует включать, т.е. между (сумма 21,2) и решаем, между какими пунктами его следует включать, т.е. между 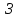 и Г, или Г и и Г, или Г и 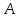 . .Чтобы это решить, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле 1. Подставляем знчения из таблицы 4 и определяем размер приращений: 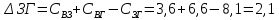 км. км.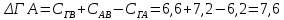 км. км.Из полученных значений выбираем минимальное, т.е.  км. км.Следовательно, пункт  должен быть между пунктами должен быть между пунктами 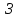 и и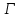 . Получаем маршрут вида: . Получаем маршрут вида: 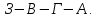 Используя этот метод и формулу приращения, определяем, между какими пунктами расположить пункт Б. 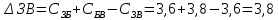 км. км.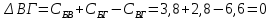 км. км.Т.к.  то пункт Б включаем между З и то пункт Б включаем между З и  . . Таким образом, окончательный порядок движения по маршруту I будет:  , длиной 21,6 км. , длиной 21,6 км.Приведём порядок движения по маршрутам I и II на рисунке 3: А Ж  А   Д   И Е   К  З Г  Б  В  I II I II Рис. 3. Порядок движения по маршрутам I и II Таким образом, мы получили маршруты I и II, длиной 28,4 км. и 21,6 км. соответственно. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
