Сбор нагрузок на плиту. Копия Сбор нагрузок на плиту. Расчёт ребристой плиты

• Название: Расчёт ребристой плиты
• Анкор: Сбор нагрузок на плиту
• Дата: 06.01.2023
• Размер: 2.77 Mb.
• Имя файла: Копия Сбор нагрузок на плиту.doc
• Тип: Курсовая; #874374
• страница: 2 из 4

2.4.3. Продольное ребро.

Подбор арматуры продольного ребра выполняем как для изгибаемого элемента таврового профиля высотой 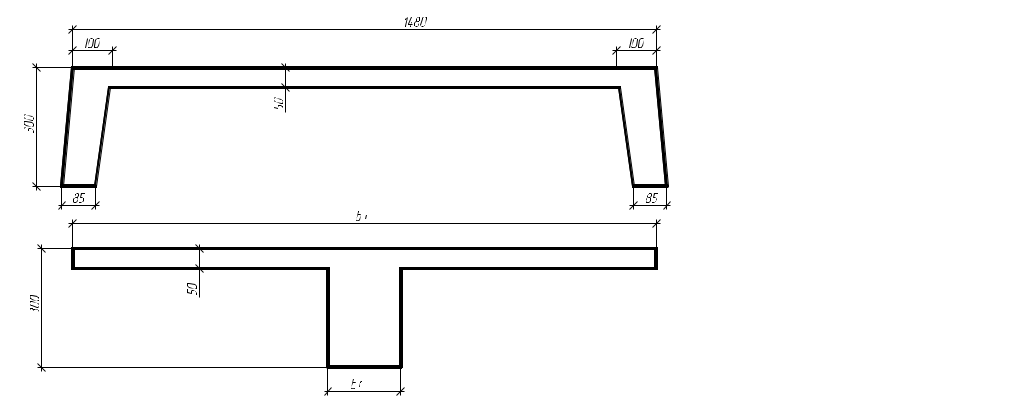фактической шириной и

.

Рис. 2.4.3.1 Расчетная схема продольного ребра.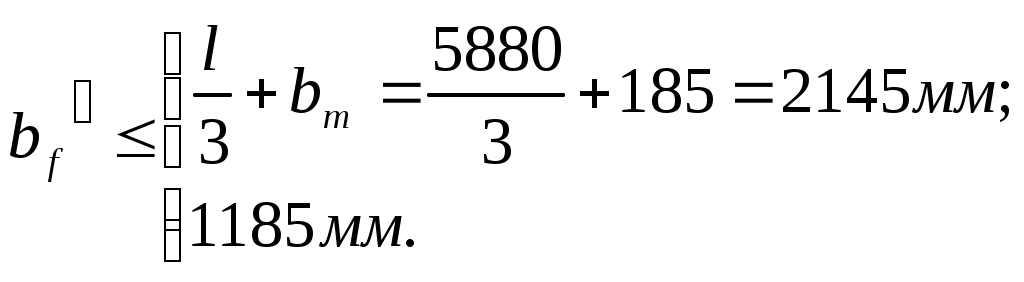




Принимаем значение, вводимое в расчёт А800 для неё нормированное .

Зададимся величиной предварительного напряжения: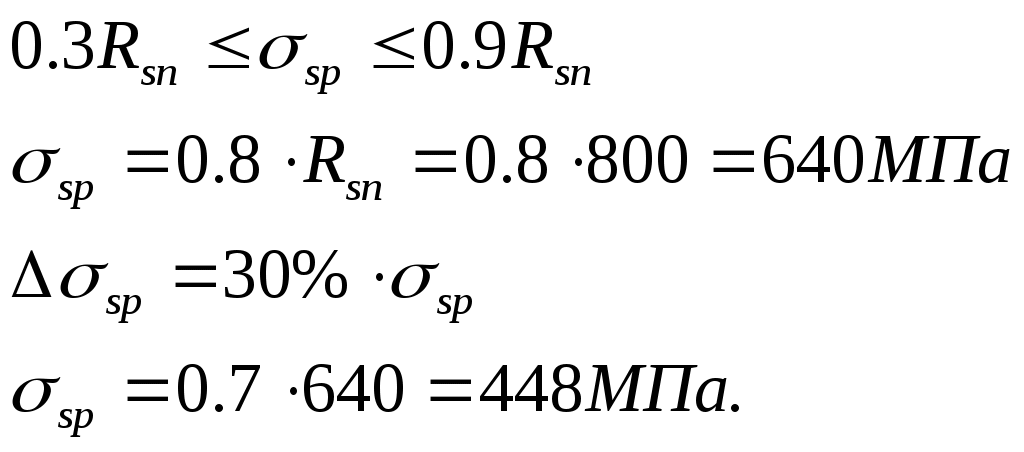




Расчёт по прочности нормальных сечений производим в зависимости от соотношений: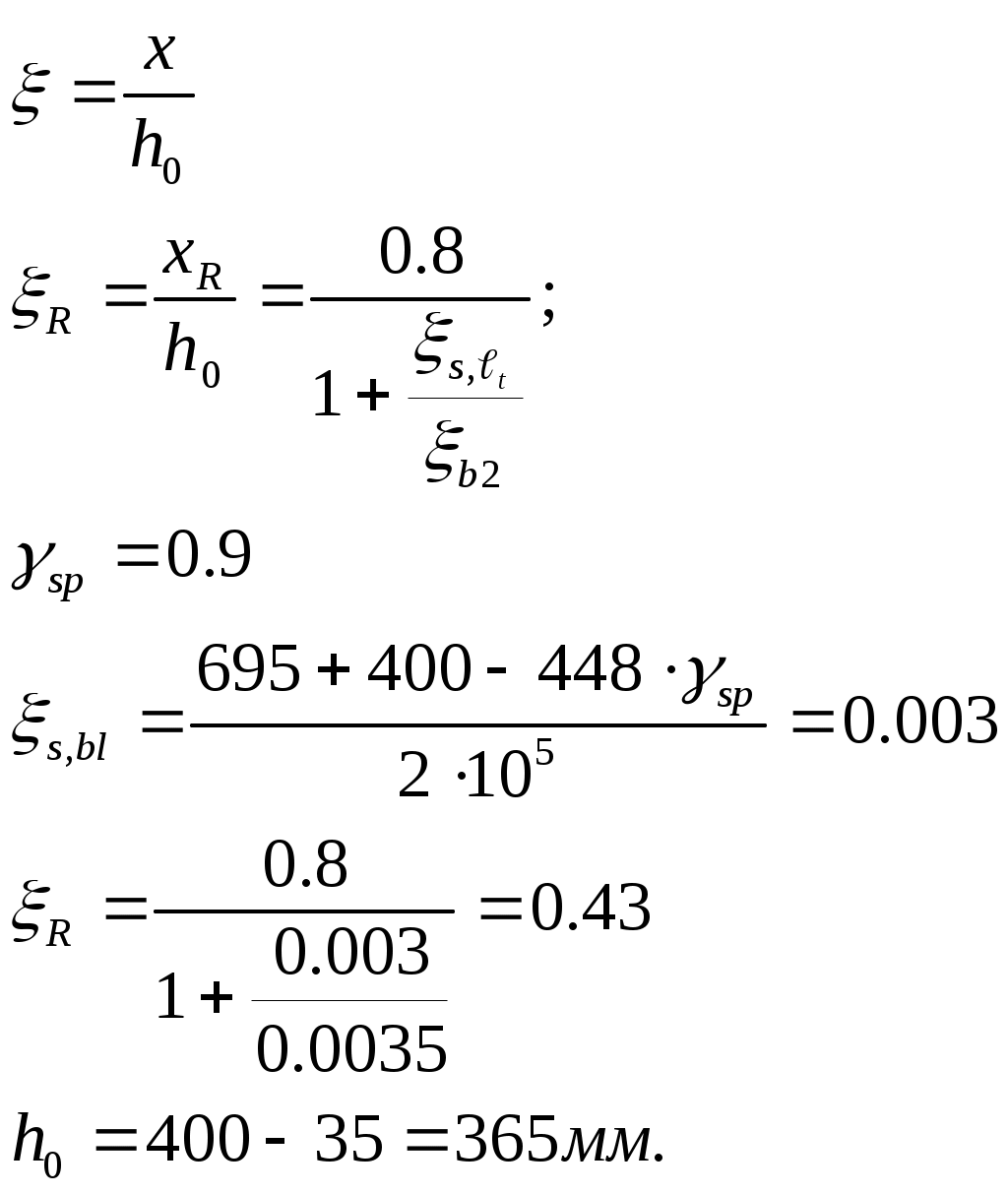


Определим положение нейтральной оси: в предположении, что сжатая арматура не требуется: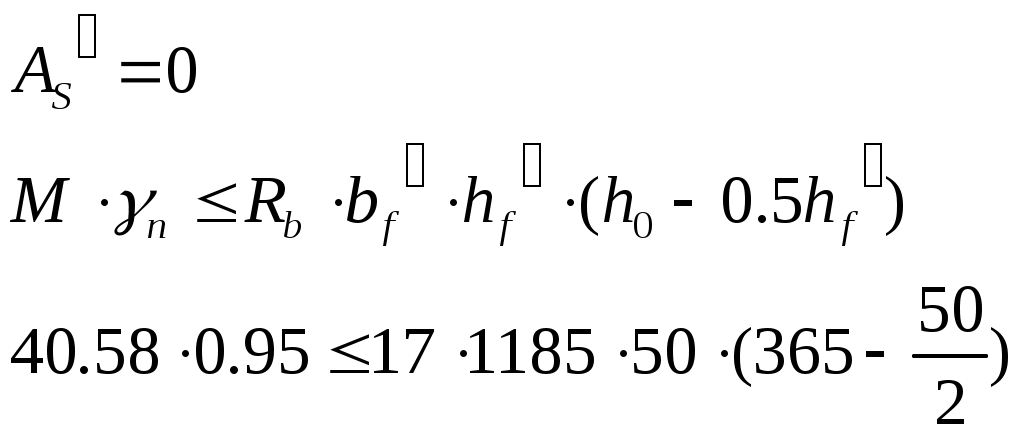



- нейтральная ось расположена в полке.
Вычисляем значения по формуле:




Сжатая арматура не требуется.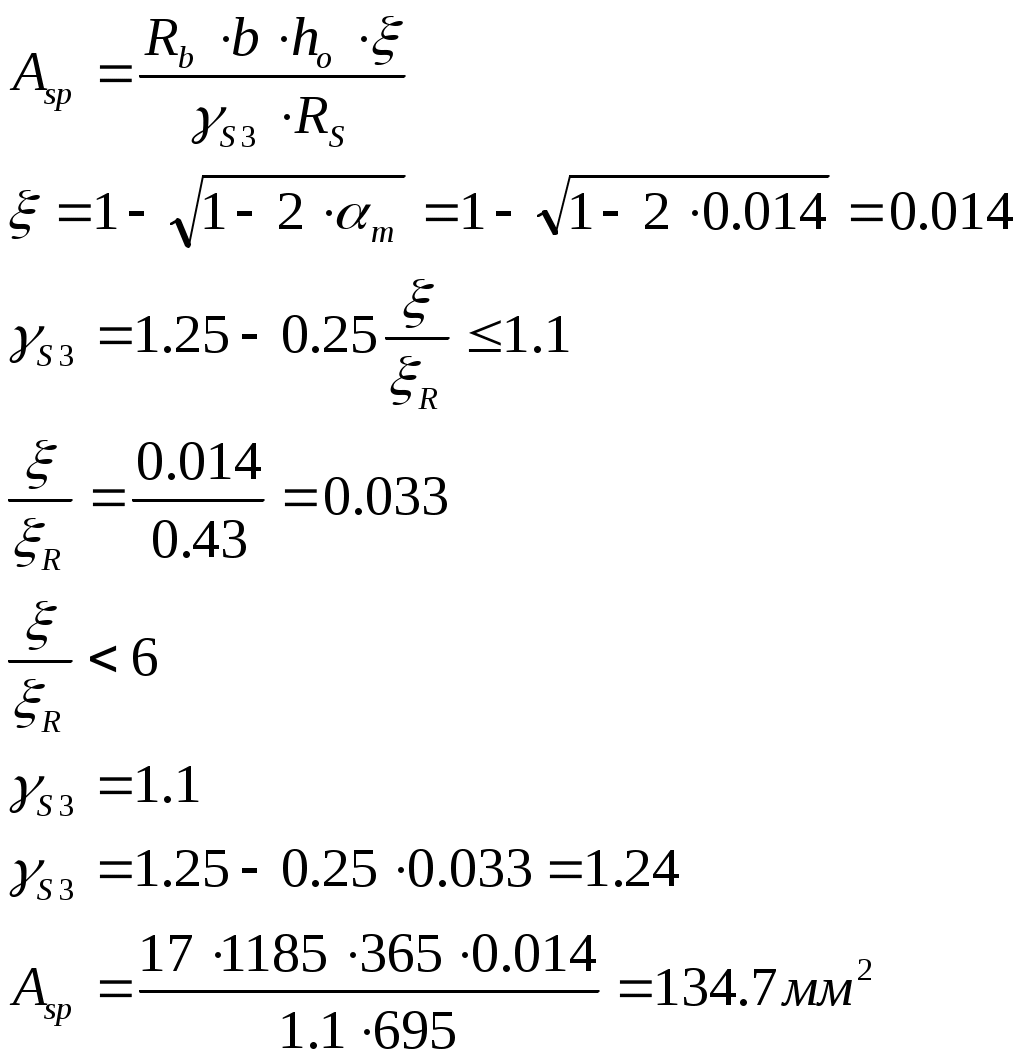


2○8 A800 ( ,

2○10 A800 ( .
В верхнем и нижнем зонах продольных рёбер для обеспечения плоского каркаса устанавливаем 2○10 A240.



Рис. 2.4.3.2 Армирование продольного ребра.

2.5. Расчет элементов плиты по наклонным сечениям.

2.5.1. Расчет поперечного ребра.

2.5.1.1. Расчет по наклонным сечениям на действие поперечной силы.

Расчет изгибаемых элементов по наклонному сечению производят из условия: ,(п.6.2.34 СП 52-101-2003) где:

Q – поперечная сила в наклонном сечении с длиной проекции «с» от внешних сил, расположенных по одну сторону от рассматриваемого сечения.

Q_b – поперечная сила, воспринимаемая бетоном в наклонном сечении.

Q_sw - поперечная сила, воспринимаемая хомутами в наклонном сечении.

, где , при этом Q_b должно быть в пределах:



При расчете элемента на действие равномерно распределенной нагрузки q , наивыгоднейшее значени «с» принимают равным: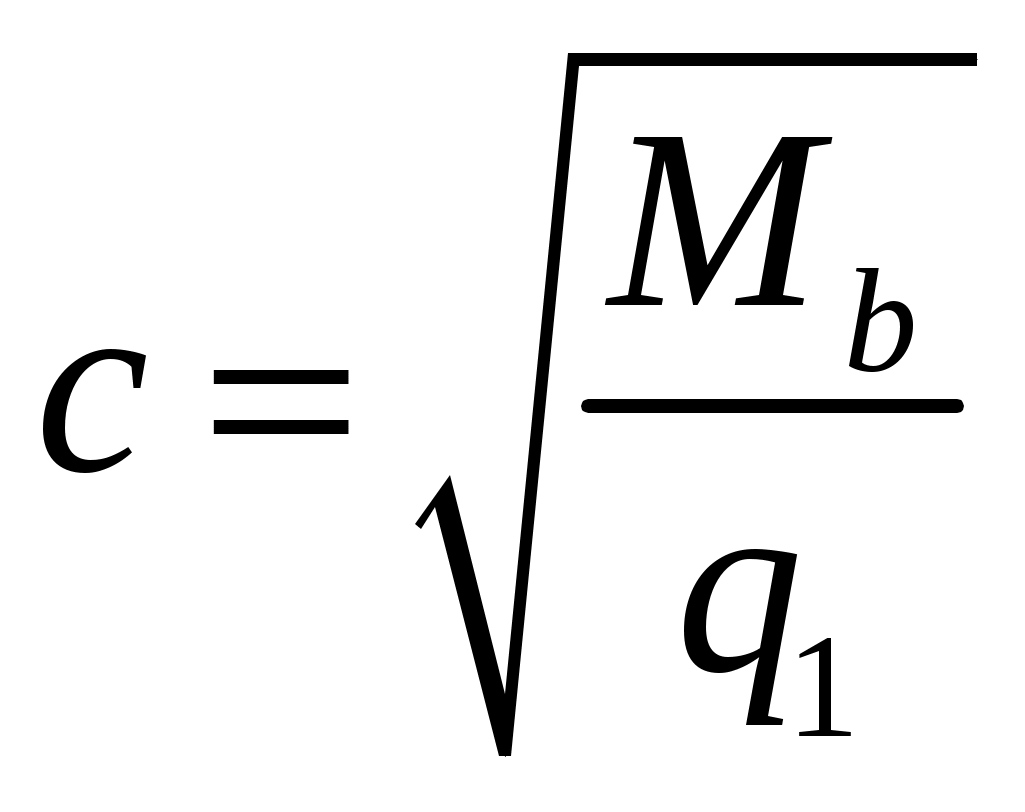

, где значение q₁ определяют следующим образом:

а) если действует сплошная равномерно распределенная нагрузка q: q₁ = q;

б) если нагрузка q включает в себя временную, которая приводится к эквивалентной по моменту равномерно распределенной нагрузки g_v:

q₁ = q – 0,5g_v, при этом Q = Q_max – q_1c, где Q_max – поперечная сила в опорном сечении.



Рис. 2.5.1.1.1 Нагрузки на поперечное ребро и эпюра изгибающего момента.





Определим эквивалентную нагрузку, действующую на поперечное ребро. Для этого определим расчётные нагрузки, действующие на наклонные сечения: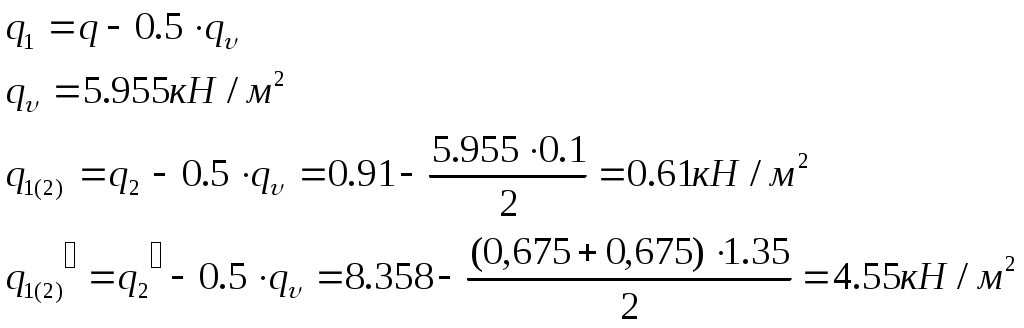



Эквивалентность достигается по моменту в середине пролёта.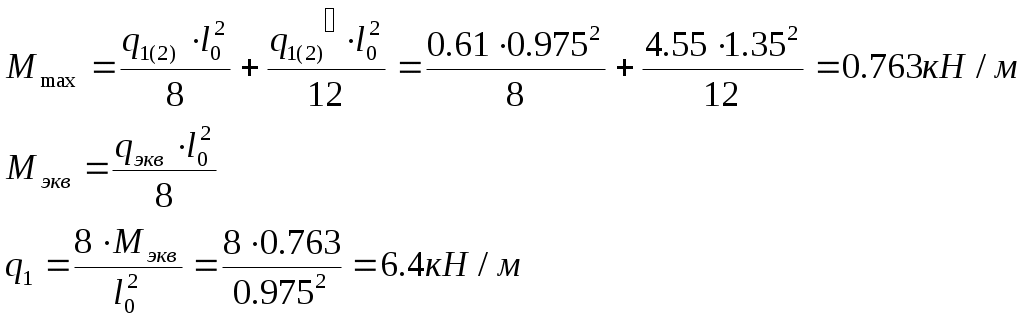



Определим, нужно ли, устанавливать поперечную арматуру по расчёту. Для этого необходимо проверить выполнение следующих условий: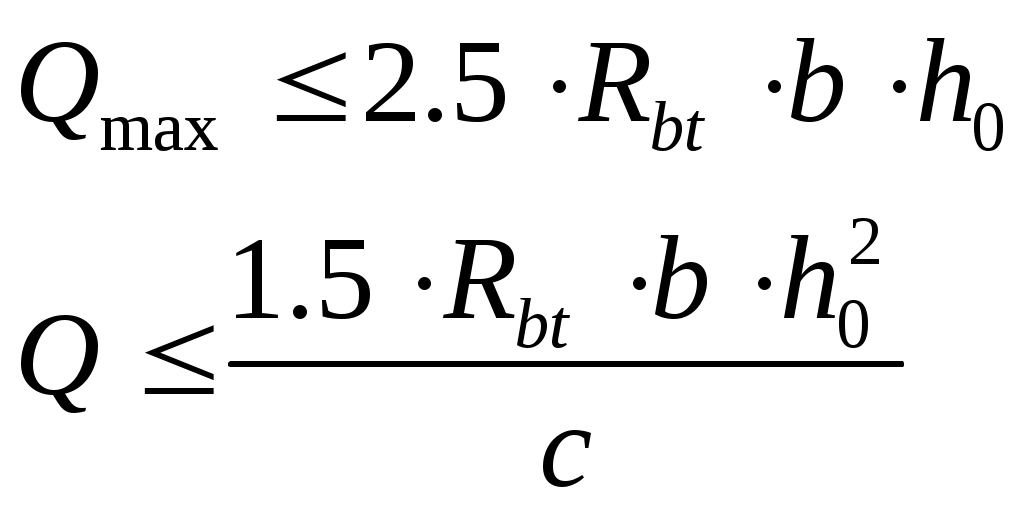



- где, Qmax – перерезывающая сила в опоре;

R_bt – прочность бетона на растяжение, для бетона B30: R_bt=1.15МПа.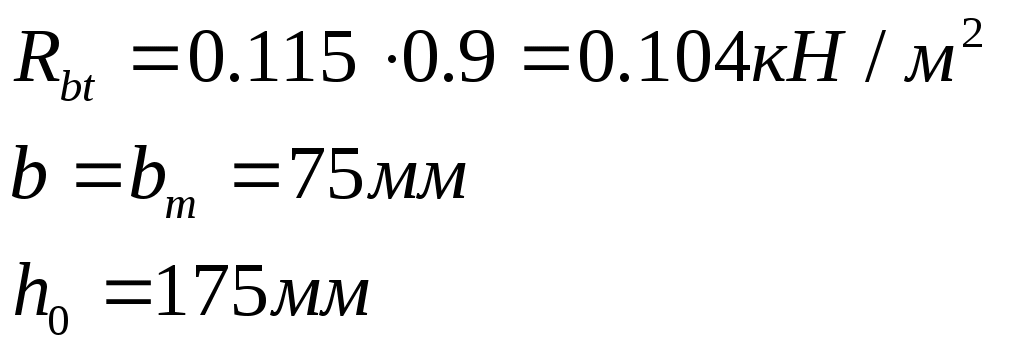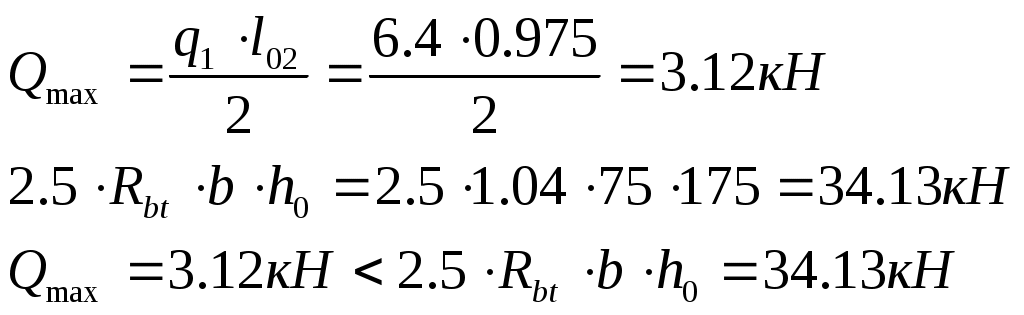




Определим величину c: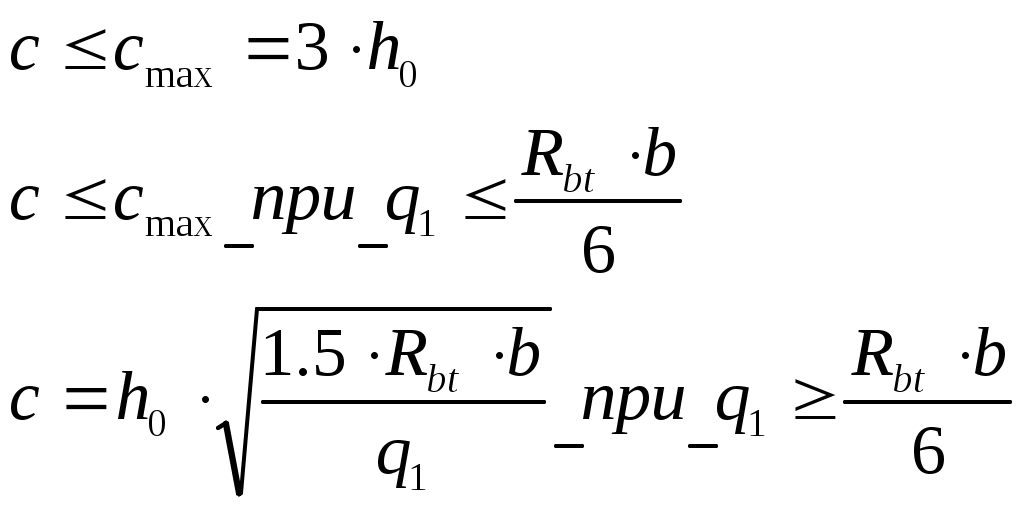





Тогда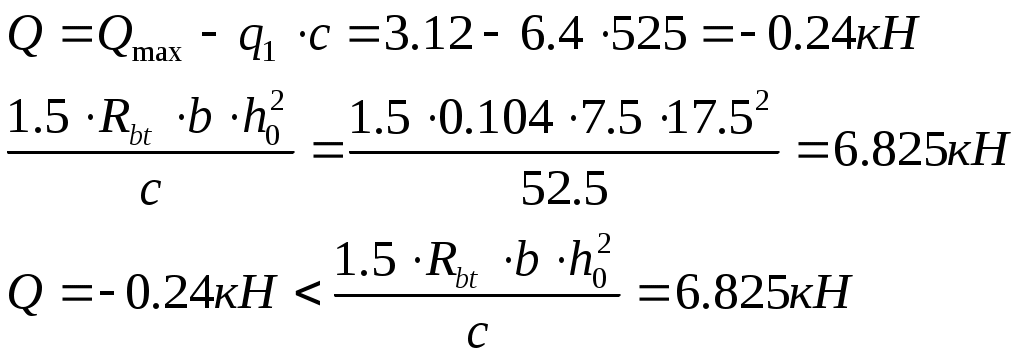



Условие выполняются, т.е. поперечная арматура по расчёту не требуется.

Т.к. высота балки >150мм поперечную арматуру необходимо установить конструктивно. Зададимся шагом поперечной арматуры: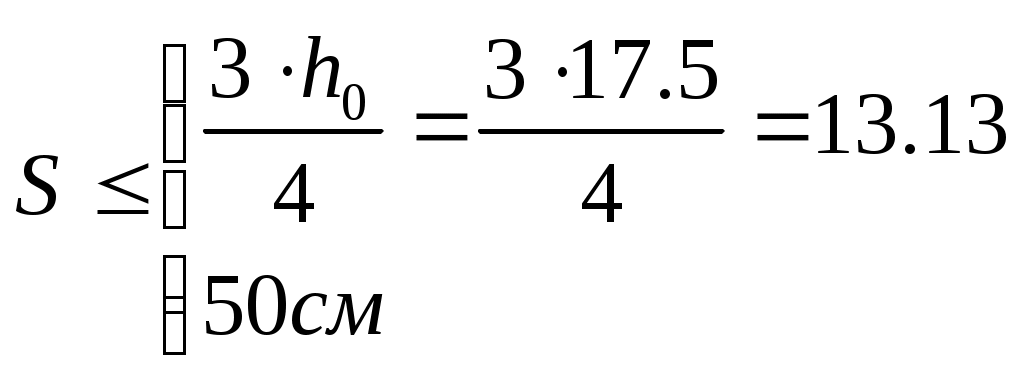



Примем шаг поперечной арматуры S=100мм.

Из условия свариваемости при диаметре продольной арматуры ○10 А400 определим наименьший допустимый диаметр поперечной арматуры 3мм. Примем арматуру - ○3 B500.
Таблица 2.5.1.1 Спецификация арматуры поперечного ребра.

Позиция	Наименование КР – 1	Количество шагов	Масса единицы участка, кг	Общая масса, кг
1	10 А400 ГОСТ 62.27 – 80* L = 1240	1	1,24*0,617 = 0,765	0,765
2	3 В500 ГОСТ 62.27 – 80* L = 150	13	0,15*0,052 = 0,0078	0,101
3	10 А240 ГОСТ 62.27 – 80* L = 1240	1	1,24*0,617 = 0,765	0,765

Рис. 2.5.1.1.2 Арматурный каркас поперечного ребра.

2.5.1.2. Расчет по наклонной сжатой полосе на действие поперечной силы.

Прочность сжатой полосы обеспечена, если: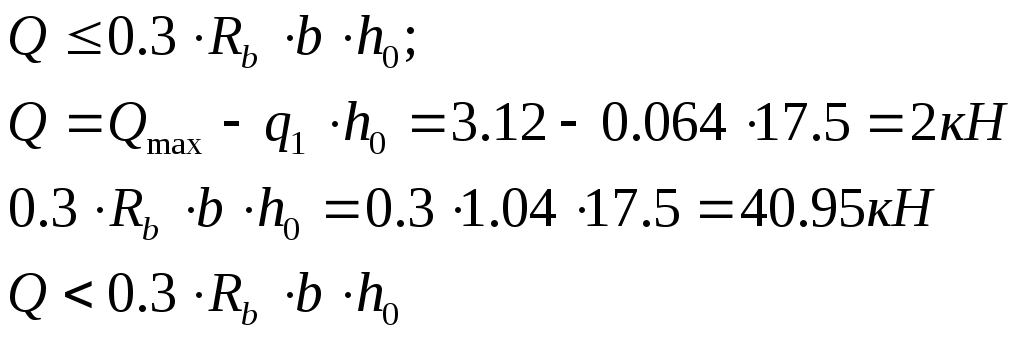



Условие выполняется, прочность между наклонными сечениями обеспечена.
2.5.2 Расчет продольного ребра.

2 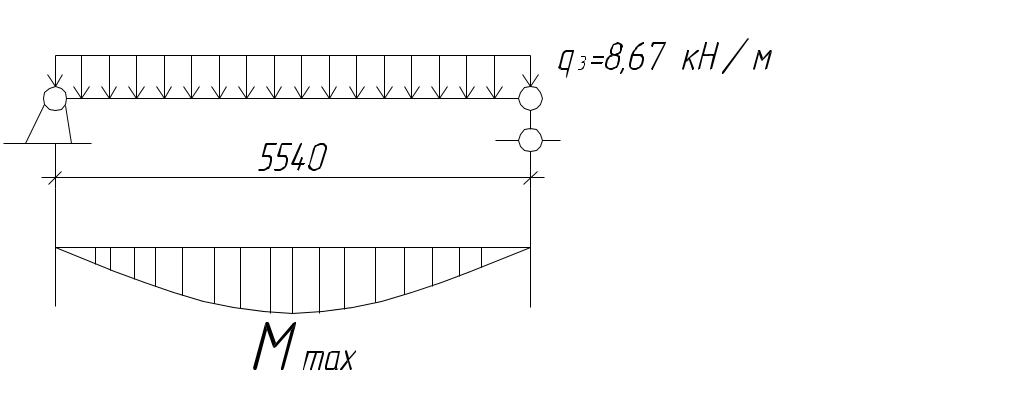.5.2.1 Расчет продольного ребра по наклонному сечению на действие поперечной силы.

Определим эквивалентную нагрузку, действующую на продольное ребро. Для этого определим продольные нагрузки, действующие на продольное сечение.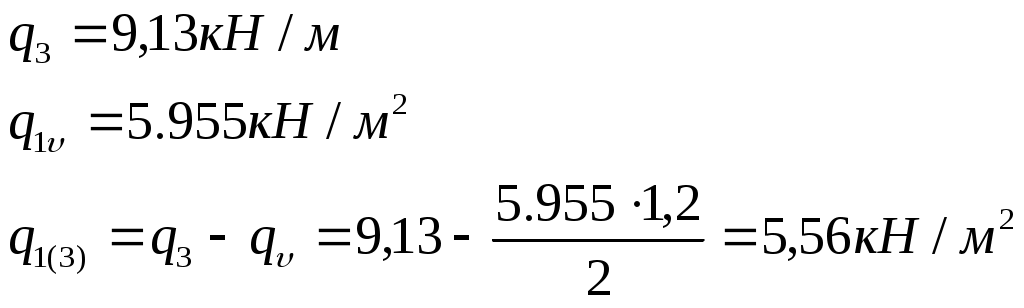



Определим, нужно ли устанавливать поперечную арматуру, Для этого необходимо проверить поперечную арматуру на выполнение следующих условий: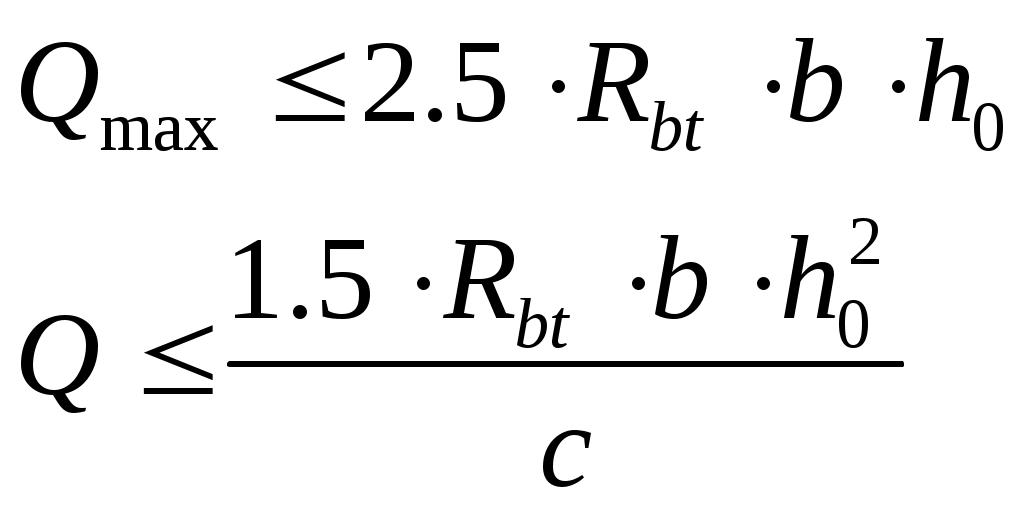



Q – перерезывающая сила на опоре.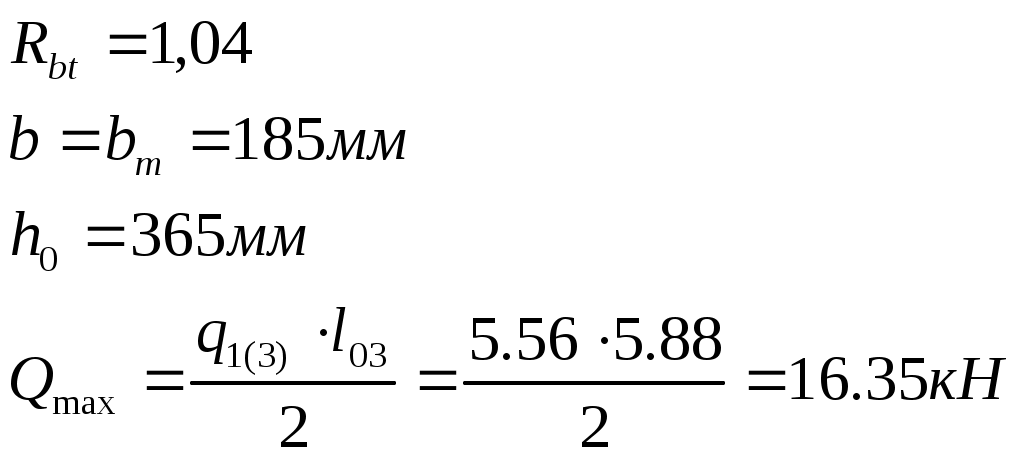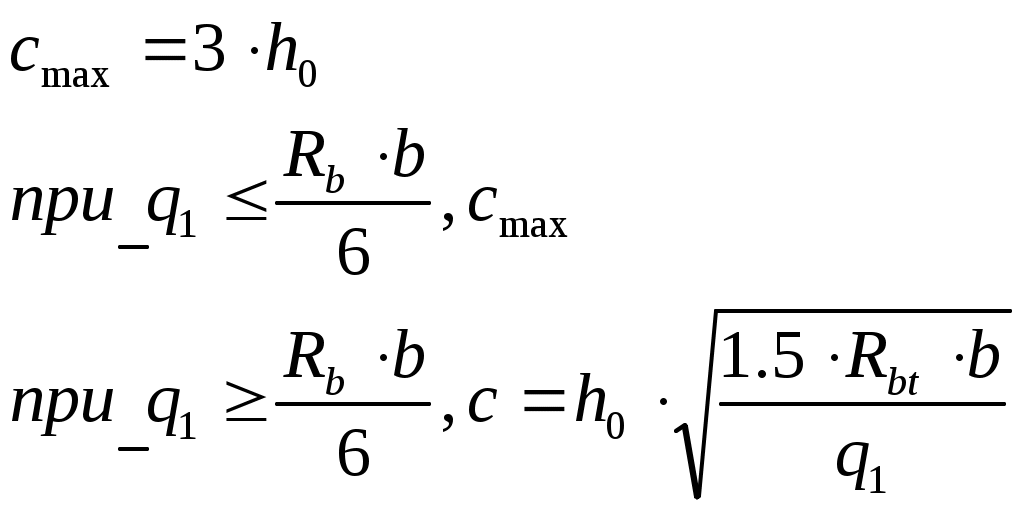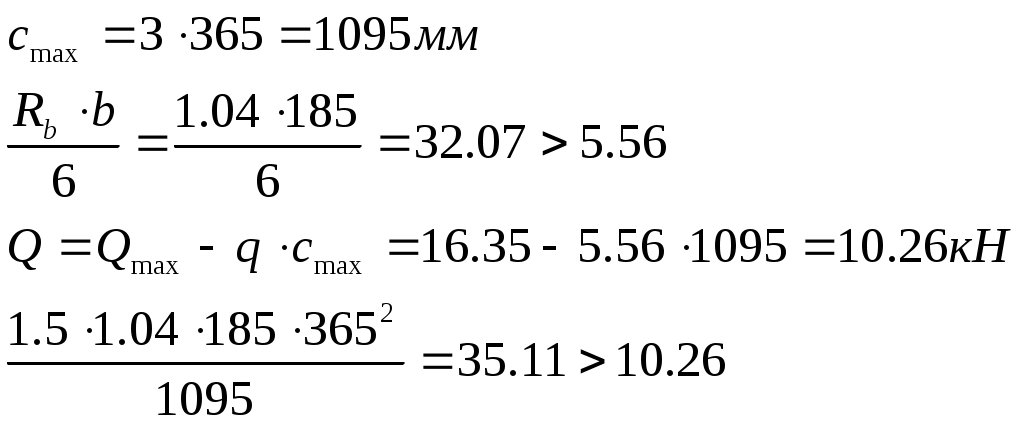








Условие выполняется, поперечной арматуры не требуется.

Устанавливаем её конструктивно:

Определим требуемую интенсивность хомутов приопорного участка. При действии на элемент только равномерно распределённой нагрузки Q. Требуемая интенсивность хомутов определяется в зависимости 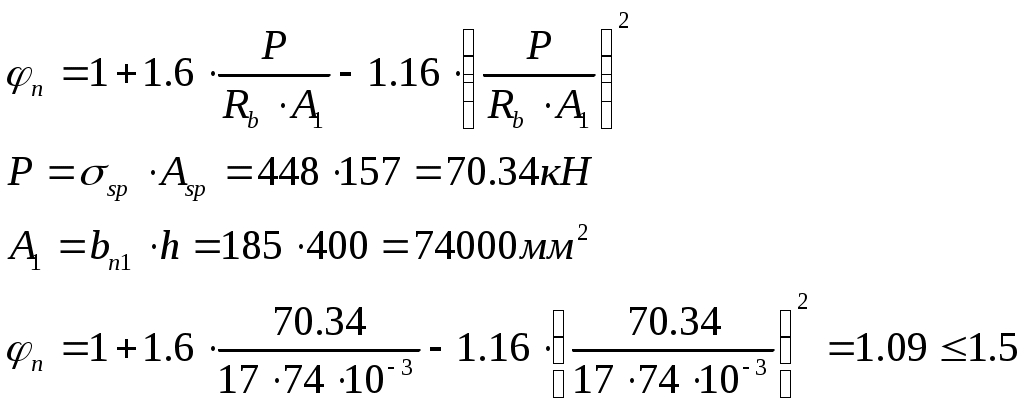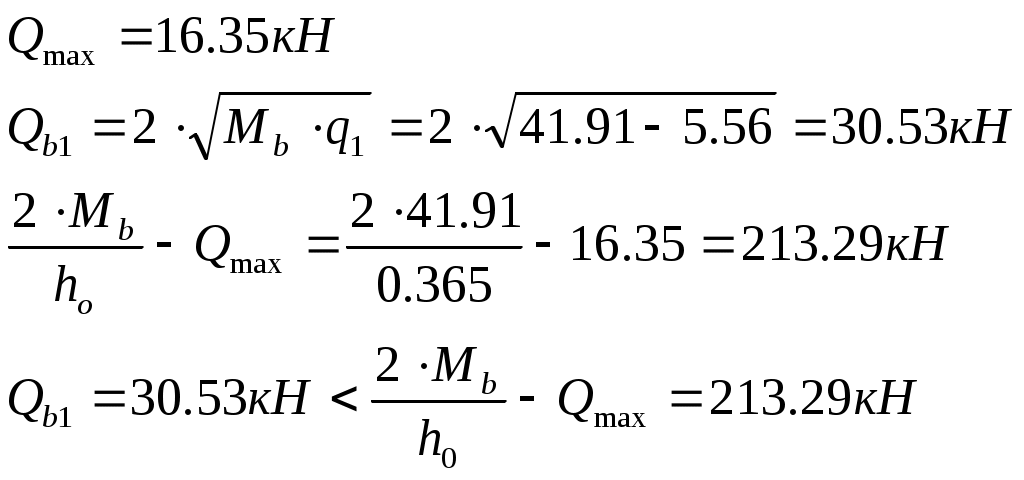, следующим образом:







Условие выполняется, тогда: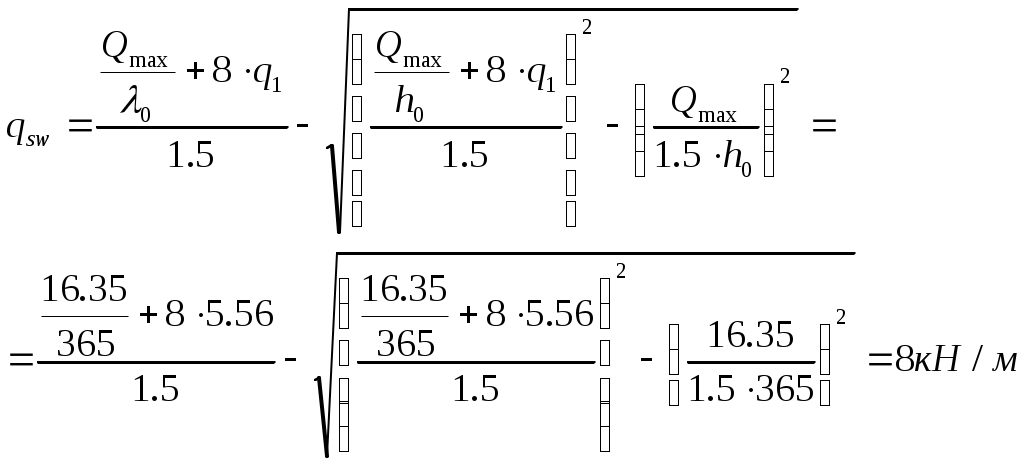



Принимаем :



У опоры: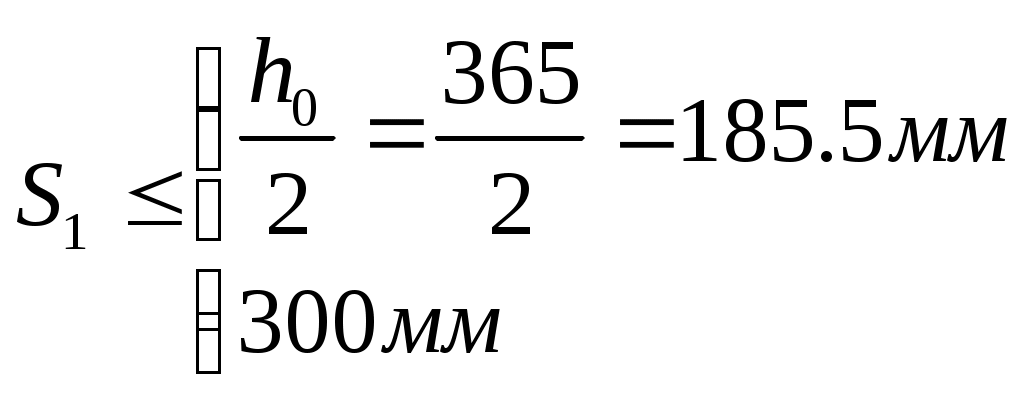



Принимаем .

В пролёте: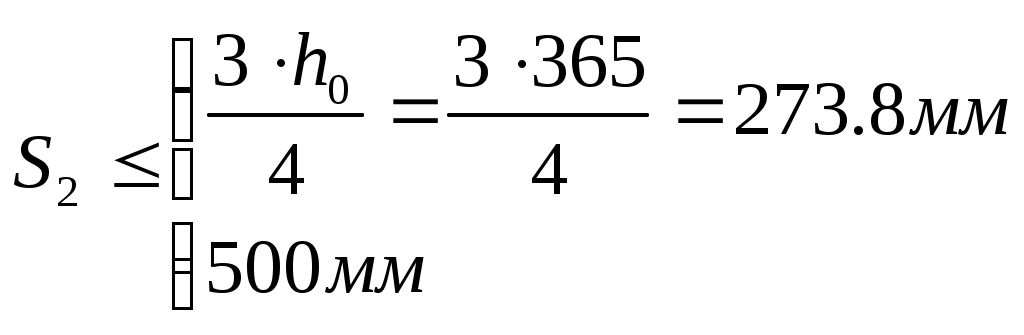



Принимаем .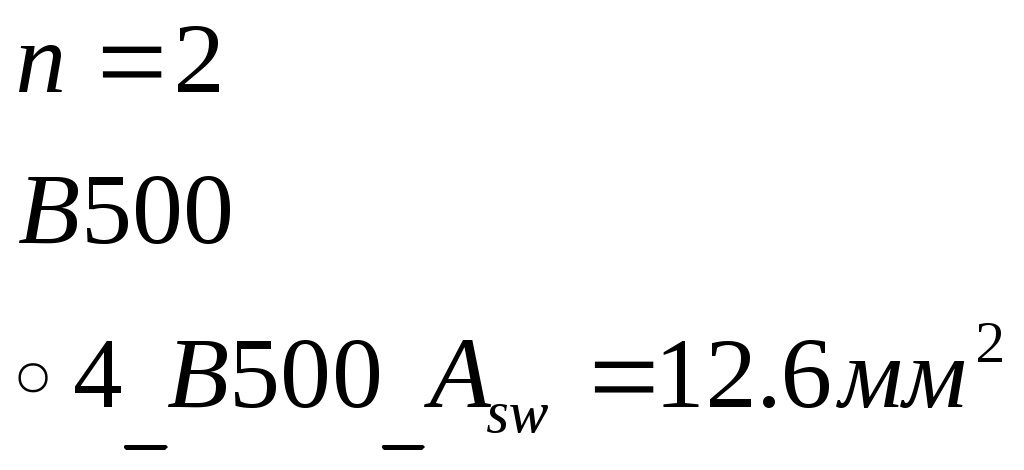



При действии на элементарно распределённой нагрузки, длина участка с интенсивностью хомутов 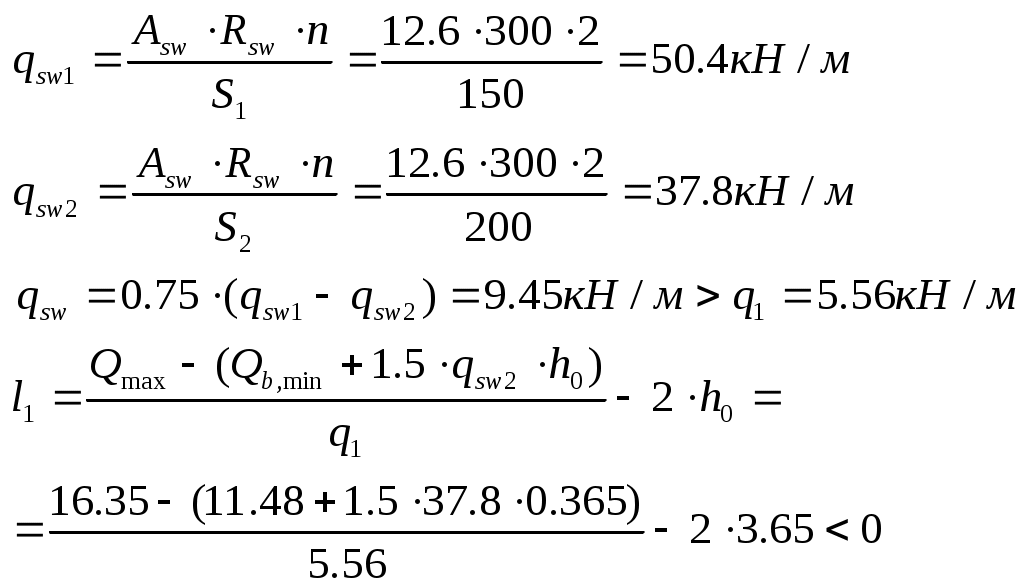примем не менее . Значение определим в зависимости , следующим образом:



Принимаем

2.5.2.2.Расчёт продольного ребра по наклонной сжатой полосе на действие поперечной силы.

Прочность сжатой полосы обеспечена, если :



Условие выполнено, прочность между наклонными сечениями обеспечена.

2 .6. Расчет элементов плиты по II-ой группе предельных состояний.

2.6.1. Определение геометрических характеристик приведенного сечения.

Рис. 2.6.1.1 Приведенное сечение.

Определим геометрические характеристики в приведённом сечении. Приведённое сечение включает в себя площадь сечения и бетона и площадь сечения всей продольной арматуры с коэффициентом привидения арматуры .

Площадь приведенного сечения определяется: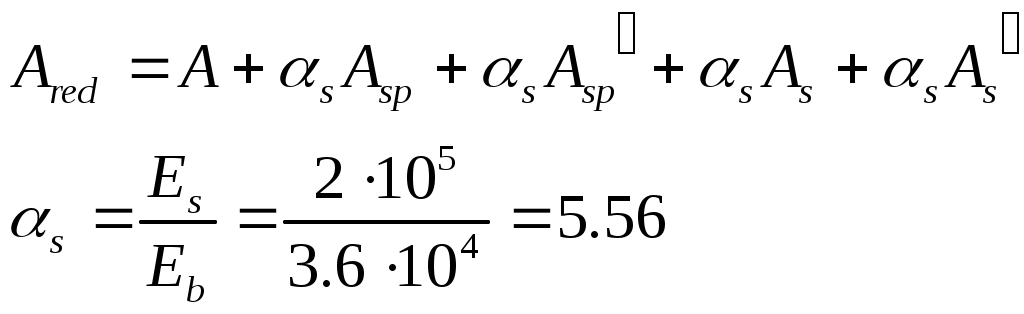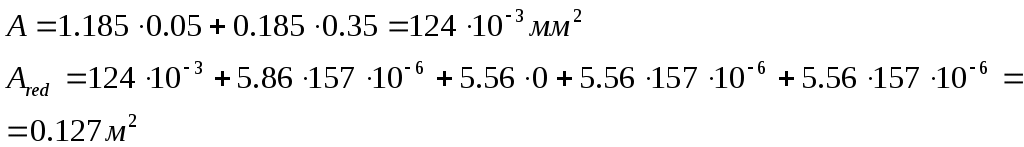





Статический момент приведенного сечения относительно оси «х»:



Расстояние от центра тяжести приведенного сечения до растянутой в стадии эксплуатации грани:




Момент инерции приведенного сечения: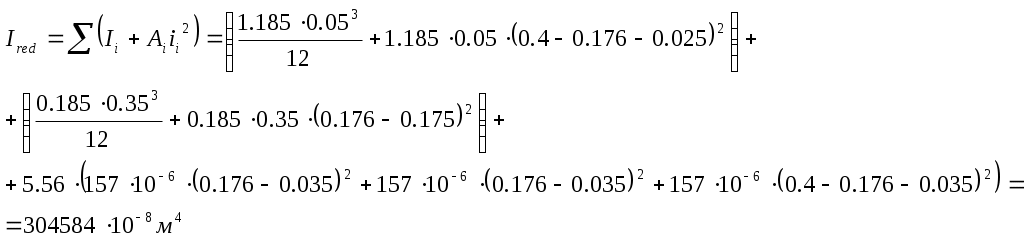



Момент сопротивления приведенного сечения по нижней грани:



Момент сопротивления приведенного сечения по верхней грани:


Расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести приведенного сечения:


Расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести приведенного сечения: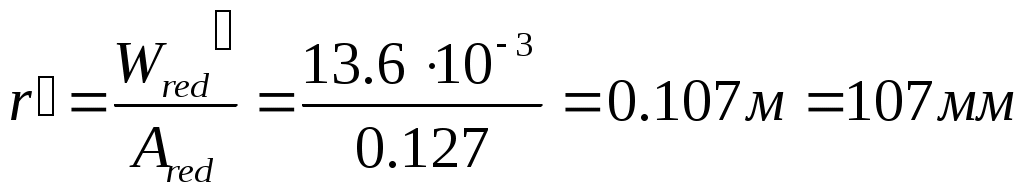



Упругопластический момент сопротивления по растянутой зоне:

, где - коэффициент принимаемый по СП 52-102-2004.

Упругопластический момент сопротивления по сжатой зоне:



где 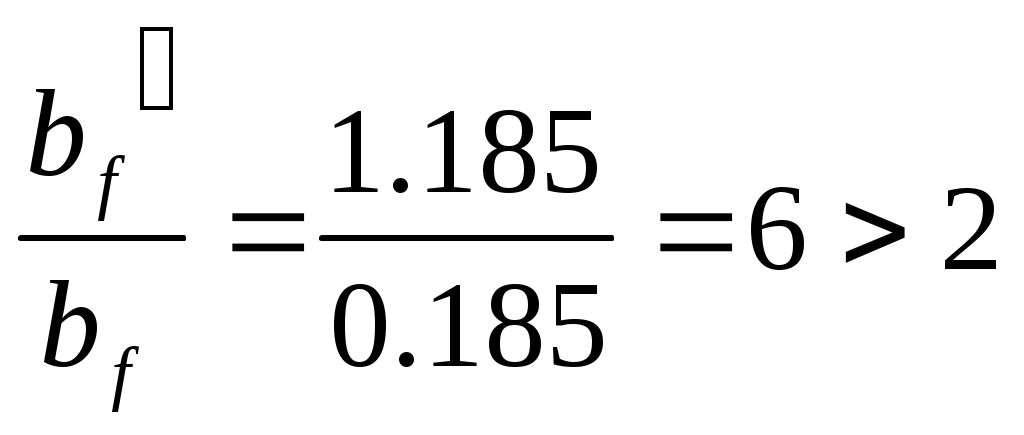; т.к.
2.6.2. Определение потерь предварительного напряжения арматуры продольного ребра.

При расчете предварительного напряжения конструкций, следует учитывать снижение предварительного напряжения в следствии потерь предварительного напряжения до передачи усилий натяжения на бетон (1-ые потери) и после передачи усилия натяжения на бетон (2-ые потери).

1-ые потери включают:

- потери от релаксации предварительного напряжения в арматуре;

- потери от температурного перепада при термической обработки конструкции;

- потери от деформации анкеров и деформации формы;

2-ые потери включают:

- потери от ползучести у усадки бетона.

Существуют 2 вида предварительного напряжения арматуры:

- механический;

- электротермический.

В нашем случае для расчета принимается электро-термический вариант предварительного напряжения арматуры.
1.Потери от релаксации в арматуре определяют по формуле:

;

2.Потери от температурного перепада , определяемого как разность температур натягиваемой арматуры в зоне нагрева и устройства, воспринимающего усилие натяжения. При отсутствии достоверных данных следует принимать :


3.Потери от деформации стальной формы (упоров) при неодновременном натяжении арматура на форму:

.



4.Потери от деформации анкеров, расположенных у натяжных устройств: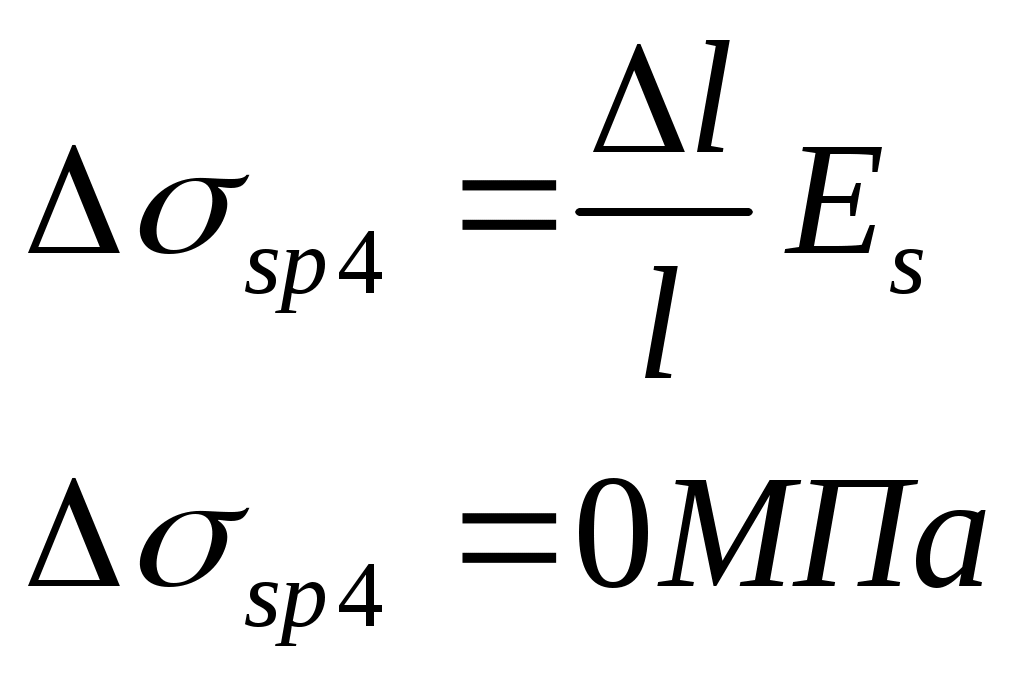



Сумма первых потерь :

5.Потери от усадки бетона :

, где - деформация усадки бетона. Для бетонов класса В35 и ниже (В30)

6.Потери напряжений в рассматриваемой напрягаемой арматуре от ползучести бетона: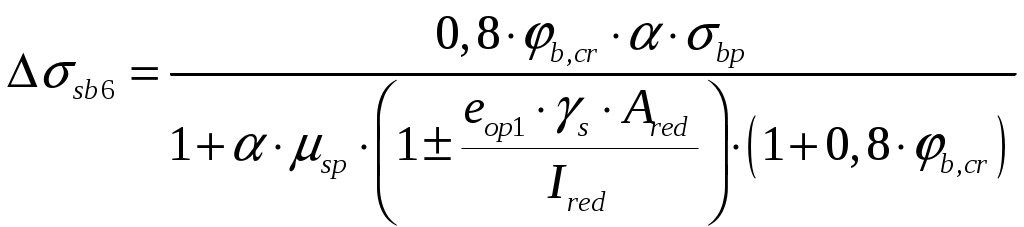



где - напряжение бетона на уровне центра тяжести рассматриваемой напрягаемой арматуры, определяется как для упругих материалов согласно формуле:



- усилие предварительного обжатия с учетом

1-ых потерь.

- сумма первых потерь.

- эксцентриситет усилия Р₍₁₎ относительно центра тяжести приведенного сечения.

Усилие предварительного обжатия бетона с учетом первых потерь:



Предварительное напряжение в бетоне при передаче предварительного усилия обжатия , определяемого с учетом первых потерь не должны превышать:

если напряжение уменьшается или не изменяется при действии новых нагрузок

если напряжение увеличивается при действии внешних нагрузок

Сжимающие напряжения учитываются со знаком «+», а растягивающие со знаком « - ».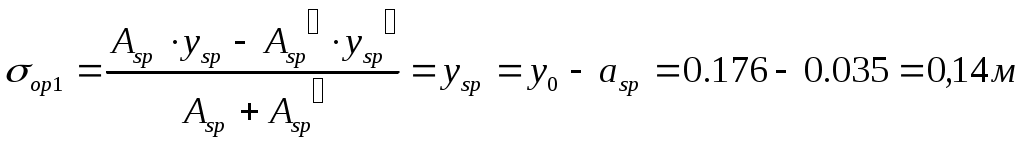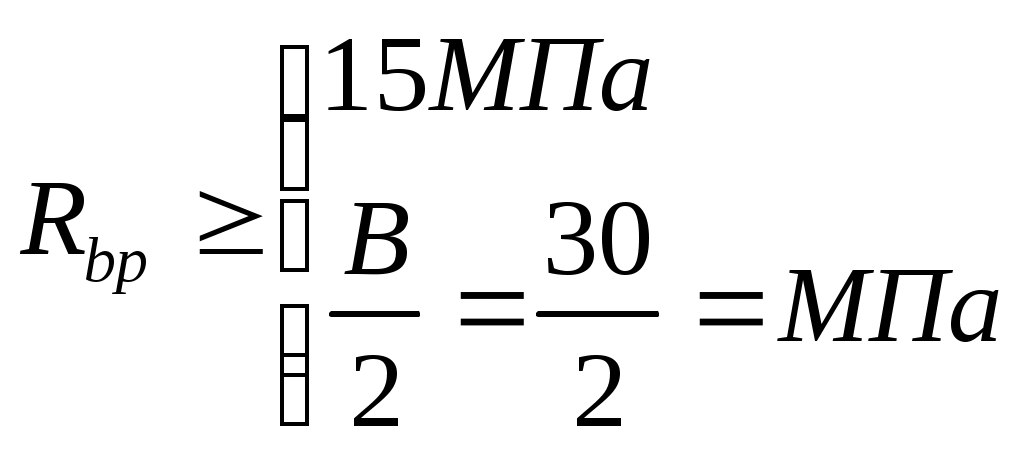





принимаем ;

После того как плиту вынимают из формы, она начинает воспринимать собственный вес, который является изгибающим моментом: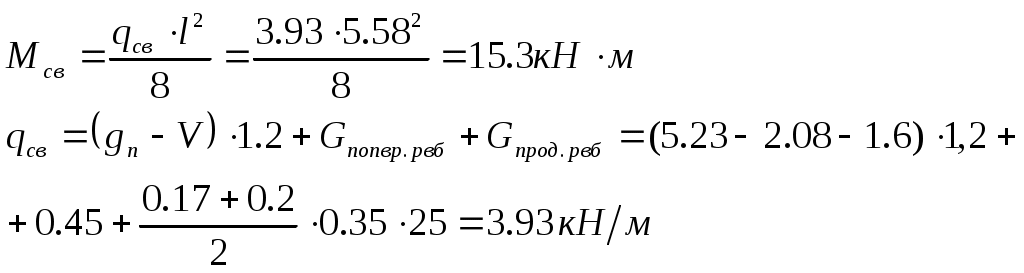



Напряжение обжатия в бетоне с учетом собственного веса плиты:







- коэффициент ползучести принимаемый по СП 52-102-2004 в зависимости от влажности.



Сумма 2-х потерь:

Суммарные потери:

Суммарные потери напряжения в арматуре следует принимать

более 100 МПа.

Итоговое напряжение в арматуре:



Усилие обжатия с учетом всех потерь напряжения определяется по формуле:



Напряжение в бетоне на уровне арматуры :



здесь будут действовать растягивающие усилия, поэтому:



т.е. сжимающие напряжение в ненапрягаемой арматуре мы принимаем равным 0.