Расчет на растяжение и сжатие. Расчет ступенчатого стержня на растяжение сжатие
 Скачать 43.78 Kb.
|
|
Министерство сельского хозяйства и образования РФ ФГБОУ ВО «Мичуринский государственный аграрный университет» Кафедра: Транспортно-технологических машин и основ конструирования Расчетно-графическая работа №1 по Сопротивлению материалов на тему: «Расчет ступенчатого стержня на растяжение сжатие» Вариант 15
Мичуринск 2021 г. Для расчета статически определимого стержня согласно заданию принимаем 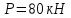 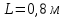 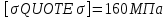 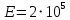 1 Построение эпюры продольных сил Разбиваем стержень на грузовые участки и нумеруем их римскими цифрами. Применяя метод сечений, определим продольные силы на каждом участке из условия равновесия отсеченных частей стержня. На первом участке 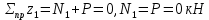 На втором участке 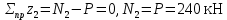 На третьем участке 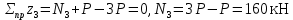 На четвертом участке 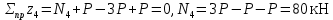 Из условия равновесия всего стержня находим реакцию опоры 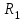 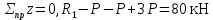 По полученным данным строим эпюру продольных сил. 2 Подбор поперечных сечений стержня Используя условия прочности 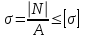 Находим площади поперечных сечений на всех основных участках: 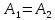 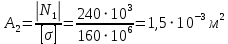 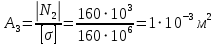 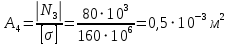 3 Построение эпюр нормальных напряжений Если на одном грузовом участке окажутся части стержня с разными поперечными сечениями, то нормальные напряжения нужно вычислять для каждой части стержня отдельно. Число участков для определения напряжения при этом увеличивается по сравнению с числом грузовых участков. Определим нормальные напряжения в рассмотренном выше стержне: 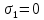 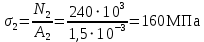 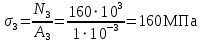 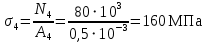 Строим эпюры нормальных напряжений по длине стержня. 4 Определение деформаций и перемещений Общее удлинение (укорочение) определим как алгебраическую сумму абсолютных деформаций каждого участка стержня: 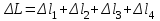 Используя закон Гука, получим: 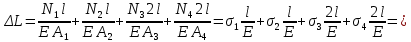 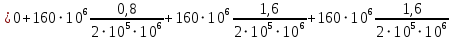 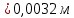 Определим перемещения граничных сечений по отношению к жестко закрепленному верхнему торцу стержня. Искомые перемещения численно равны абсолютному удлинению (укорочению) частей стержня, расположенных выше рассматриваемого сечения: 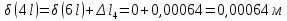 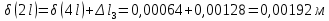 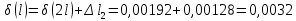 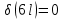 Поскольку продольные силы и площади поперечных сечений в пределах каждого участка стержня остаются постоянными, перемещения промежуточных сечений пропорциональны координатам 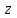 . Учитывая это, по полученным значениям перемещений строим эпюру 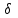 .5 Раскрытие статической неопределимости Степень статической неопределимости рассматриваемой системы 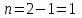 Запишем уравнение равновесия для стержня: 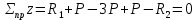 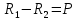 Поскольку опоры стержня абсолютно жесткие, то общая абсолютная деформация стержня равна нулю: 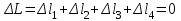 Это соотношение является условием совместности деформаций. Используя закон Гука, принимаем условия совместности деформаций в следующем виде: 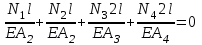 Применяя метод сечений, из условия равновесия отсеченных частей стержня найдем: 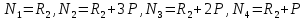 Используя полученные выражения, принимаем условия совместности деформаций: 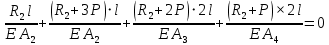 Сокращая на общие множители, подставляя значение площадей А1 , А2 ,А3 и А4, найденные ранее, приводя подобные члены, получим: 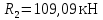 Статическая неопределимость стержня раскрыта. 6 Построение эпюр продольных сил и нормальных напряжений Зная, значение реакций R2, вычисляем продольные силы: 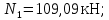 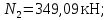 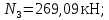 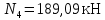 По полученным результатам строим эпюру продольных сил. Определяем нормальные напряжения в стержне: 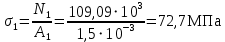 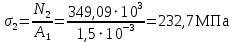 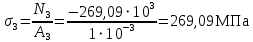 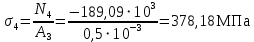 Построим эпюру нормальных напряжений. Выполняем кинематическую проверку, для чего подсчитываем абсолютную деформацию стержня: 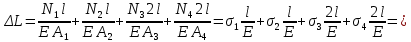 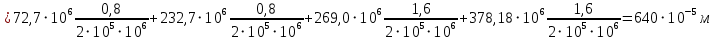Задача решена верно. Построим эпюру 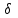для рассматриваемого стержня с двумя жестко закрепленными торцами. Начнем с верхнего торца. Его перемещение 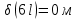 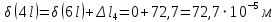 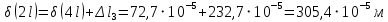 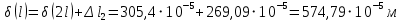  |