Расчёт сложной электрической цепи синусоидального тока. Расчёт сложной электрической цепи синусоидального тока
 Скачать 250.32 Kb. Скачать 250.32 Kb.
|
|
Кафедра электротехники ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к расчётной работе на тему: «Расчёт сложной электрической цепи синусоидального тока» Выполнил: Проверил: Вариант № 11 Самара 2018 Задание 1) Рассчитать все токи в цепи, изображенной на рисунке 1, по известным данным, приведенным в таблице 1 с помощью метода контурных токов, метода узловых потенциалов. Найти один из токов по методу эквивалентного источника. 2) Произвести проверку с помощью уравнений Кирхгофа.
Исходные величины Электрическая схема: 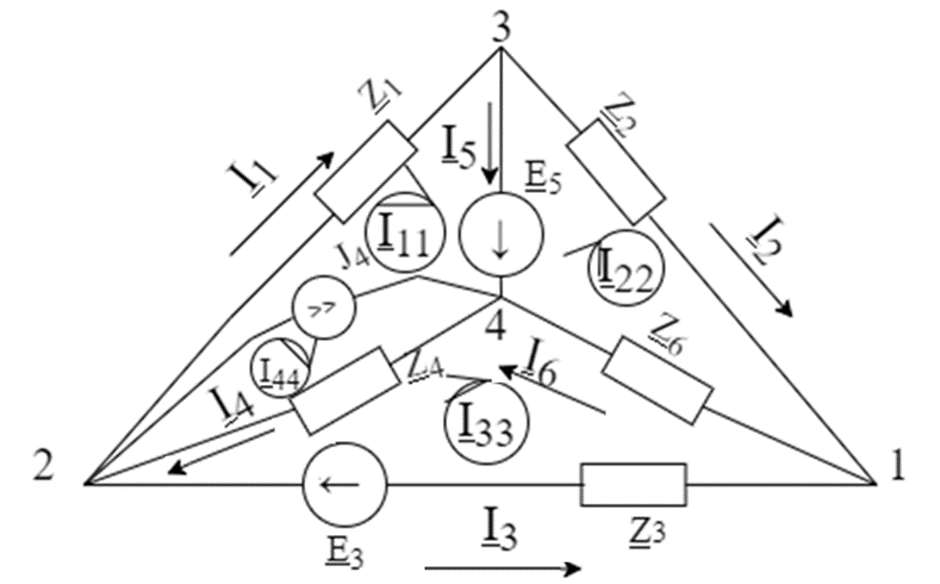 РЕФЕРАТ Пояснительная записка МЕТОД КОНТУРНЫХ ТОКОВ, МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ, МЕТОД ЭКВИВАЛЕНТНОГО ИСТОЧНИКА ЭДС, ЗАКОНЫ КИРХГОФА Объектом исследования служит сложная электрическая цепь синусоидального тока, состоящая из комплексных сопротивлений, источника ЭДС и источника тока. Цель работы: Изучить методы расчёта сложной электрической цепи В процессе работы использованы методы контурных токов, узловых потенциалов, эквивалентного источника ЭДС. В результате работы были найдены токи во всех ветвях. СОДЕРЖАНИЕ Введение…………………………………………………………………5 Метод контурных токов…………………………………………………6-8 Метод узловых потенциалов……………………………………………9-10 Метод эквивалентного источника ЭДС ……………………………….11-13 Проверка уравнениями Кирхгофа……………………………………...14 Проверка методом баланса мощностей ……………………………….15 Мгновенные значения токов ветвей………………………...…………16 Векторная диаграмма………………………………………...…………17 Мгновенные значения тока и ЭДС одной ветви………………………18 Заключение………………………………………………………………19 Список литературы……………………………………………………...20 ВВЕДЕНИЕ В данной работе представлены 3 способа нахождения токов в ветвях сложной электрической цепи:
Затем была произведена проверка с помощью законов Кирхгофа и условия баланса мощностей Метод контурных токов Для дальнейших расчётов, преобразуем исходные значения ЭДС и силы тока в комплексные значения. e3=1,41*sin(ωt)→ E3= 1,41*ej*0=1,41, B e5=2,82*sin(ωt-90⁰)→E5=2,82*e-j*90⁰=-2,82j, B j4=0,141*cos(ωt) → J4=0,141*ej*90⁰=0,141j, A Найдём действующие комплексные значения E3= 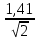 = 1, B = 1, BE5= 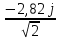 = -2j, B = -2j, BJ4= 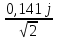 = 0,1j, A = 0,1j, A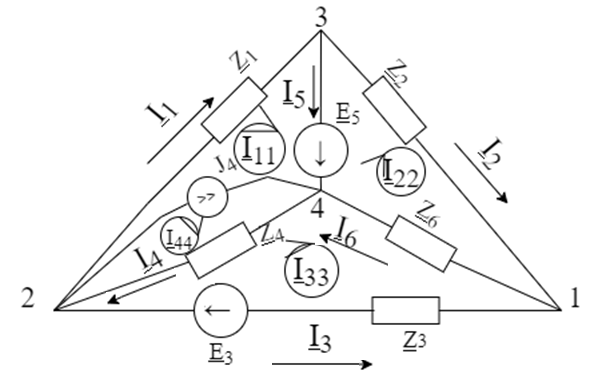 Определим количество независимых контуров, а соответственно и число уравнений: n= m – k + 1, где
N = 7 – 4 + 1= 4 Запишем систему уравнений в общем виде 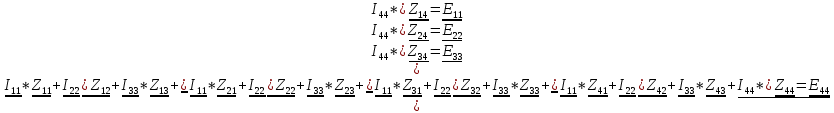 (1) (1)Рассчитаем контурные сопротивления Zij и Zii Z11 = Z1 + Z4 = 5 – j5 Z22 = Z2 + Z6 = 3 + j4 + j10 = 3 + j14 Z33 = Z3 + Z4 + Z6 = 10 + j10 – j5 = 10 + j5 Z12 = Z21 = 0 Z13 = Z31 = -Z4 Z14 = Z41 = Z4 Z24 = Z42 = 0 Z23 = Z32 = -Z6 Z34 = Z43 = - Z4 Рассчитаем контурные ЭДС E11 = E5 = -2j E22 = -E5 = 2j E33 = E3 = 1 E44 = 0 Запишем систему, подставив значения ЭДС, сопротивлений и, учитывая, что I44=J4=0,1j. 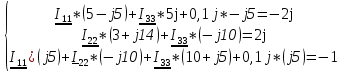 Решив данную систему, получаем: I11 = 0,171 – 0,227j I22 = 0,129 + 0,059j I33 = -0,0009 + 0,044j Запишем выражения для нахождения токов ветвей I1 = I11 I2 = I22 I3 = -I33 I4 = I11 – I33 + J4 I5 = I11 – I22 I6 = -I33 + I22 Посчитаем искомые токи ветвей I1 = 0,171 – 0,227j, A I2 = 0,129 + 0,059j, A I3 = -0,0009 + 0,044j, A I4 = 0,172 - 0,171j, A I5 = 0,042 – 0,286j, A I6 = -0,13 + 0,015j, A Метод узловых потенциалов  Примем потенциал в узле 3 φ3=0, тогда потенциал в узле 4 φ4= Е5=2j, B Запишем систему уравнений в общем виде: 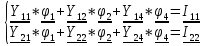 Найдём узловые комплексные проводимости узлов Y11 = 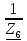 + + 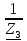 + + 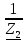 = = 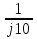 + + 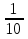 + + 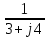 = 0,22 – 0,26j = 0,22 – 0,26jY22 = 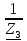 + + 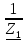 + + 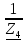 = = 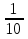 + + 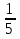 + + 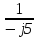 = 0,3 +0,2j = 0,3 +0,2jY12 = Y21 = 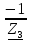 = = 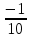 = -0,1 = -0,1 Y14 = Y41= 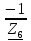 = = 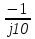 = 0,1j = 0,1jY24 = Y42= 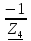 = = 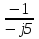 = -0,2j = -0,2jНайдём узловые токи I11 =  + + 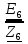 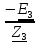 = =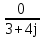 + +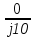 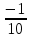 = -0,1 = -0,1I22 = 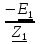 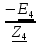 + + 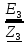 – J4 = 0,1 – 0,1j – J4 = 0,1 – 0,1j Подставим в систему значения проводимостей и токов 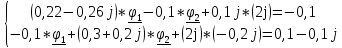 Решим систему относительно неизвестных потенциалов φ1 и φ2 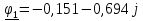 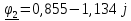 Запишем закон Ома в общем случае для каждой ветви и рассчитаем токи ветвей 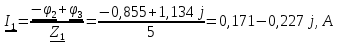 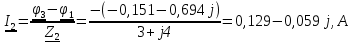 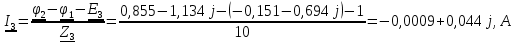 I4 = 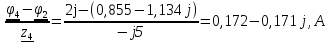 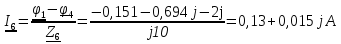 Ток в ветви с идеальным источником ЭДС найдём по 1 закону Кирхгофа I5 = I1 – I2 = 0,042 – 0,286j, A Метод эквивалентного источника ЭДС 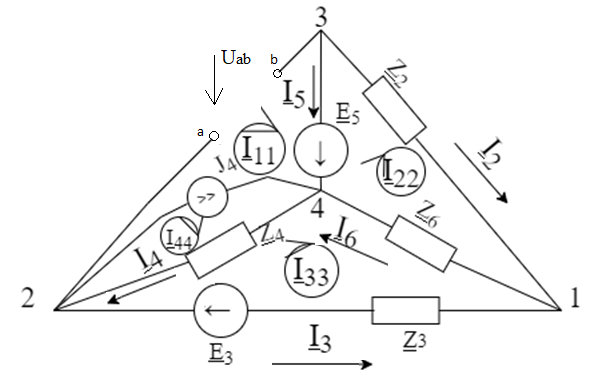 Разомкнём ветвь, где протекает ток I1, а остальную часть цепи заменим эквивалентным источником ЭДС Еэкв с внутренним сопротивлением Zэкв. Для нахождения тока I1, необходим рассчитать напряжение на обрыве a, для чего необходимо рассчитать напряжение на элементе с сопротивлением Z4, а для этого необходимо рассчитать ток в этой цепи. Рассчитаем ток в новой цепи, используя метод контурных токов Запишем систему уравнений в общем виде 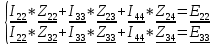 Рассчитаем контурные сопротивления Zij и Zii Z22 = Z2 + Z6 = 3 + 14j Z23 = Z32 = -Z6 = -10j Z24 = Z42 = 0 Z33 = Z3 + Z4 + Z6 = 10 + 5j Z34 = Z43 = -Z4 = 5j Рассчитаем контурные ЭДС Е22 = -Е5 = 2j Е33 = Е3 = 1 Запишем систему, подставив значения контурных ЭДС и сопротивлений, а также учитывая, что I44 = J4 = 0,1j 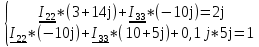 Решив данную систему, получаем: I22 = 0,174 + 0,132j I33 = 0,084 + 0,132j Рассчитаем ток I4 для нахождения напряжения на элементе с сопротивлением Z4: I4 = I33 – J4 = 0,084 + 0,132j – 0,1j = 0,084 + 0,032j, A Тогда U4 = I4 * Z4 = 0,162 – 0,42j, В Рассчитаем значение ЭДС эквивалентного источника Eэкв Еэкв = Uab = E5 + U4 = 0,162 – 2,414j, В Рассчитаем входное сопротивление цепи между зажимами разомкнутой ветви, считая оставшуюся часть цепи пассивной (источники ЭДС E3 и E5 закорочены, ветвь с источником тока J4 разомкнута) Схема для расчёта Zэкв: 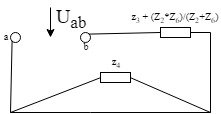 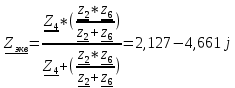 Тогда искомый ток 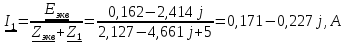 Проверка решения законами Кирхгофа I закон Кирхгофа Узел 1 I1 – I2 – I5 = 0 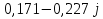 – ( – (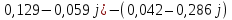 = 0 = 00 = 0 Узел 2 I2 + I3 – I6 = 0 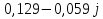 + + 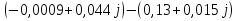 = 0 = 00 = 0 Узел 3 I4 – I1 – I3 – J4 = 0 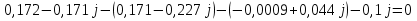 0 = 0 Узел 4 I5 + I6 – I4 = 0 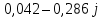 + + 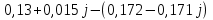 = 0 = 00 = 0 Ⅱ закон Кирхгофа 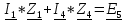 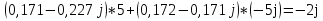 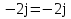 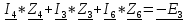 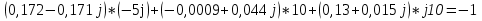 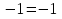 Проверка решения методом баланса мощностей 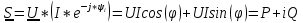 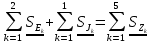 Принимая начальную фазу тока и напряжения за 0, рассчитаем комплексную мощность для источников ЭДС 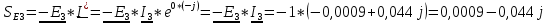 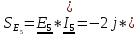 0,042 – 0,286j) = -0.572 - 0.0084j 0,042 – 0,286j) = -0.572 - 0.0084jКомплексная мощность источника тока: 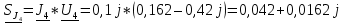 Комплексные мощности на сопротивлениях: 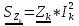 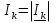 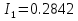 ; ; 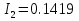 ; ; 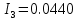 ; ; 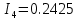 ; ; 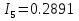 ; ; 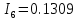 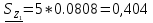 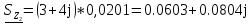 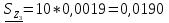 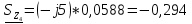  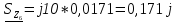 Условие баланса: 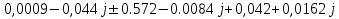 = =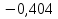 + +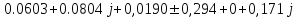 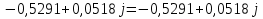 Мгновенные значения токов ветвей 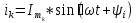 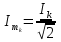 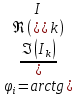 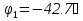 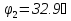 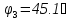 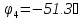 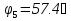 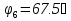 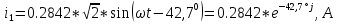 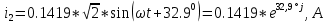 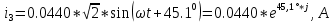 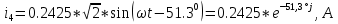 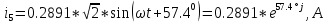 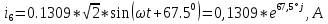 Запишем значения в полярной форме ρ = 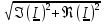 ρ1 = 0.2842 ρ4 = 0.2425 ρ2 = 0.1419 ρ5 = 0.2891 ρ3 = 0.0440 ρ6 = 0.1309 Векторная диаграмма 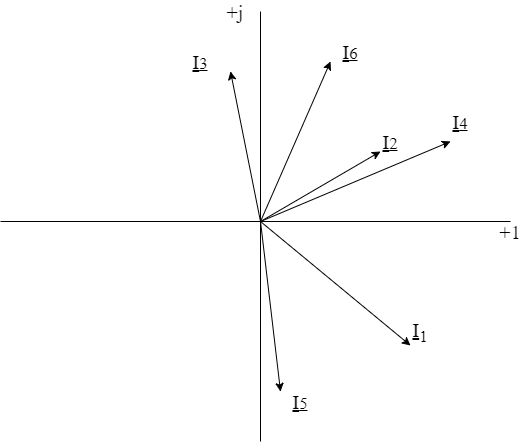 Мгновенные значения тока и ЭДС одной ветви Построим на графике мгновенные значения ЭДС и тока 5 ветви: 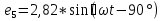 ; ;  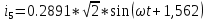 ωt 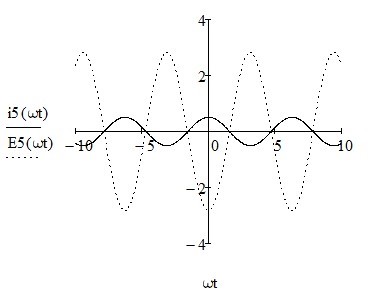 Заключение В данной работе был проведён расчёт сложной электрической цепи синусоидального тока тремя методами:
В результате, полученные разными методами значения токов оказались одинаковыми. Проведённые проверки законами Кирхгофа и методом баланса мощностей подтвердили правильность решения. Список литературы
|
