Расчетно-Графическая работа. Расчет стержней на прочность и жесткость при растяжениисжатии, кручении и изгибе
 Скачать 131.45 Kb. Скачать 131.45 Kb.
|
|
Минобрнауки России Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный технологический институт (технический университет)» УГНС «Химическая и биотехнология» Специальность 18.03.01 «Химическая технология» Профиль «Химическая технология органических веществ» Факультет Химической и биотехнологии Кафедра Механики Учебная дисциплина Сопротивление материалов Курс 2 Группа 296 РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2 Тема РАСЧЕТ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ РАСТЯЖЕНИИ-СЖАТИИ, КРУЧЕНИИ И ИЗГИБЕ Студент Преподаватель Луцко А.Н. Оценка за РГР _________________________ _______________________ (подпись преподавателя, дата) Санкт-Петербург 2021 Оглавление Введение 1. Задача №1 Расчет напряжений и деформаций при растяжении (сжатии) 1.1. Определение размеров поперечного сечения 1.2. Определение размеров сечения квадратной формы ступенчатого стержня. 1.3. Расчет экономии материала. 1.4. Расчет абсолютного удлинения. 2. Задача №2 Расчет на прочность и жесткость при кручении. 2.1. Определение круглого поперечного сечения из условия прочности. 2.2. Расчет распределения касательных напряжений по поперечному сечению. 2.3. Определение размеров вала с кольцевым сечением. 2.4. Расчет распределения напряжений по кольцевому поперечному сечению. 2.5. Расчет экономии. 2.6. Расчет вала круглого сечения на жесткость. 2.7. Проверка жесткости. 3.Задача №4 Расчет на прочность и жесткость при изгибе 3.1.Определение размеров прямоугольного поперечного сечения 3.2. Сравнение по массе балок прямоугольного и двутаврового поперечных сечений и выбордвутавра 3.3. Определение нормальных напряжений по высоте опасного сечения балкипрямоугольного и двутавровогосечений 3.4. Определение касательных напряжений по высоте опасного сечения балкипрямоугольного и двутавровогосечений 3.5. Проверка на прочность по касательным напряжениям балок прямоугольного идвутавровогосечений Введение Дано: 1. Расчетные схемы стержней, подвергаемых растяжению-сжатию, кручению, изгибу; 2. Эпюры внутренних усилий, построенные в расчетно-графической работе №1; 3. Допускаемые напряжения при растяжении (сжатии) – [𝜎]=170 МПа, при кручении – [𝜏]=85 МПа, при изгибе – [𝜎]=170 МПа, [𝜏]=85 МПа; 4. Модуль продольной упругости 𝐸=2∙1011 Па, сдвига 𝐺=8∙1010 Па; 5. Допускаемый относительный угол закручивания [∆𝜑𝑙]=1,2∙10−3 рад/м, допускаемый прогиб [𝑦]=𝑙/300 – для однопролетной балки и [𝑦]=𝑙/100 – для консольной балки. Требуется: 1. Для стержня, подвергнутого растяжению-сжатию, определить размеры квадратного поперечного сечения при условии, что сечение постоянно по длине; определить размеры поперечных сечений на каждом грузовом участке; вычислить экономию материала при изготовлении стержня переменного сечения по длине в сравнении со стержнем постоянного сечения; построить эпюру распределения напряжений по одному из сечений; определить деформацию каждого участка стержня и построить эпюру перемещений. 2. Для подвергнутого кручению вала определить диаметры сплошного сечения – 𝑑 и кольцевого – 𝐷H и 𝐷BH при 𝛼=DBH/DH=0,8, сравнить их по весу и вычислить экономию материала при изготовлении стержня кольцевого сечения; построить эпюры распределения напряжений в опасном сечении сплошного и полого валов; определить деформацию каждого участка вала сплошного сечения, построить эпюру деформаций и проверить условие жесткости. 3. Для балки определить размеры прямоугольного поперечного сечения (при отношении 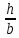 =2), подобрать по сортаменту прокатной стали (ГОСТ 8239-72) номер стандартного профиля (№ двутавра), сравнить веса стрежней этих двух форм сечения и выбрать рациональное; построить эпюры распределения напряжений 𝜎 в сечениях с максимальным изгибающим моментом 𝑀𝑚𝑎𝑥 и касательных напряжений 𝜏 в сечениях с максимальной поперечной силой 𝑄𝑚𝑎𝑥; проверить прочность балки прямоугольного сечения и двутавровой балки по касательным напряжениям; определить деформации балки, построить эпюры углов поворота сечения 𝑦′ и эпюру прогибов 𝑦 и проверить балку на жесткость. =2), подобрать по сортаменту прокатной стали (ГОСТ 8239-72) номер стандартного профиля (№ двутавра), сравнить веса стрежней этих двух форм сечения и выбрать рациональное; построить эпюры распределения напряжений 𝜎 в сечениях с максимальным изгибающим моментом 𝑀𝑚𝑎𝑥 и касательных напряжений 𝜏 в сечениях с максимальной поперечной силой 𝑄𝑚𝑎𝑥; проверить прочность балки прямоугольного сечения и двутавровой балки по касательным напряжениям; определить деформации балки, построить эпюры углов поворота сечения 𝑦′ и эпюру прогибов 𝑦 и проверить балку на жесткость.1. Задача №1 Расчет напряжений и деформаций при растяжении (сжатии) 1.1. Определение размеров поперечного сечения. 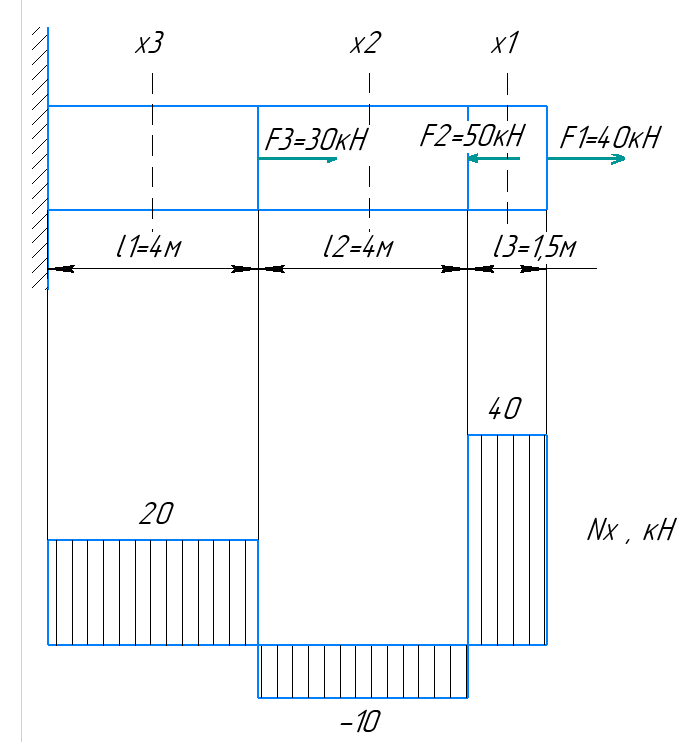 Растяжение или сжатие стержня вызывается внешними нагрузками, действующими вдоль его оси; внутренним усилием при этом будет продольная (осевая) сила. Эпюра продольных усилий позволяет определить координаты опасного сечения стержня, где 𝑁𝑥=|𝑁𝑚𝑎𝑥|=40кН на участке 0≤x≤1,5м 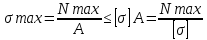 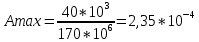 м2 м2Amax=amax2 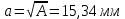 Примем аmax=16мм, Аmax=256мм 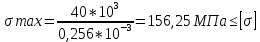 1.2. Определение размеров сечения квадратной формы ступенчатого стержня. A3= 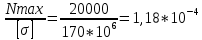 м2 м2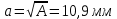 принимаем a1=11мм принимаем a1=11мм𝞂max=165,3Мпа, условие прочности выполняется. A2= 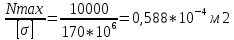 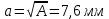 , принимаем a2=8мм , принимаем a2=8мм𝞂max=156Мпа, условие прочности выполняется. 1.3. Расчет экономии материала. 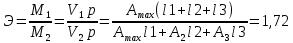 1.4. Расчет абсолютного удлинения. 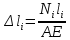 Δl1=1,17мм Δl2=-0,78 мм Δl3=1,56 мм Δl1=1,17мм Δl2=-0,78 мм Δl3=1,56 мм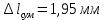 <(lсум=9500)/300 <(lсум=9500)/3002. Задача №2 Расчет на прочность и жесткость при кручении. 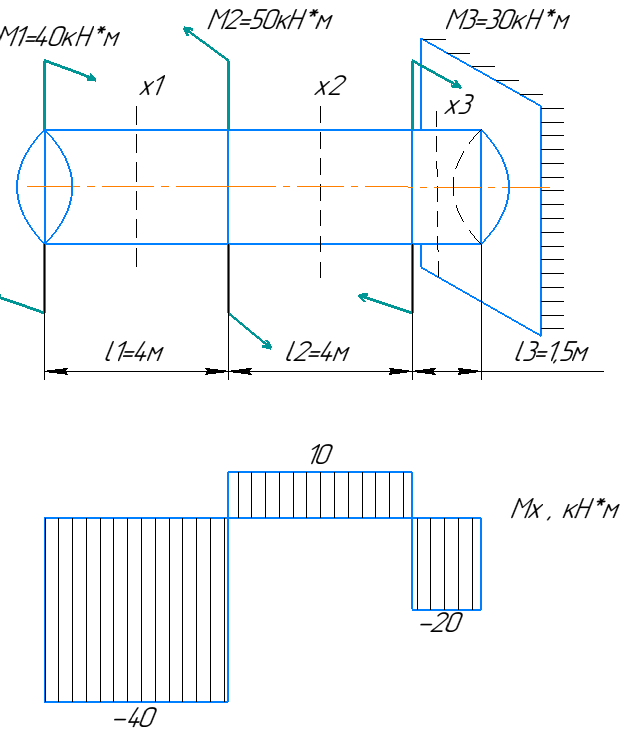 2.1. Определение круглого поперечного сечения из условия прочности. 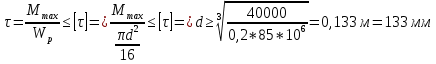 Принимаем d=133мм. 2.2. Расчет распределения касательных напряжений по поперечному сечению 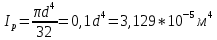 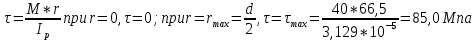 85,0Мпа=85Мпа, условие прочности выполняется. 2.3. Определение размеров вала с кольцевым сечением 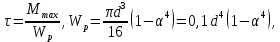 α=0,9 α=0,9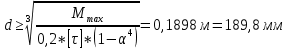 Принимаем dвнешн=190мм 𝑑внутр=0,9×190=171мм 2.4. Расчет распределения напряжений по кольцевому поперечному сечению. 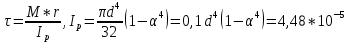 при r = 0÷d/2, τ = 0; при r =d/2 = 95мм, 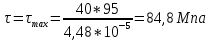 Условие прочности выполняется. 2.5. Расчет экономии. 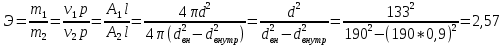 2.6. Расчет вала круглого сечения на жесткость. 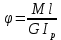 I участок:l1=4м, Mx1=-40кН*м, I участок:l1=4м, Mx1=-40кН*м, 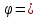 -0,046рад; -0,046рад;II участок: I2=4м, Mx2=10кН*м, 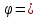 0,0112 рад; 0,0112 рад; III участок: I3=1,5м, Mx3=-20кН*м, 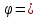 -0,00837 рад; -0,00837 рад; 2.7. Проверка жесткости. 𝜑𝚺≤[𝜑], 𝜑𝚺≤0,06рад, 𝜑𝚺=-0,0417рад ≤0,06рад Условие жесткости выполняется.  3. Расчет на прочность и жесткость балки при изгибе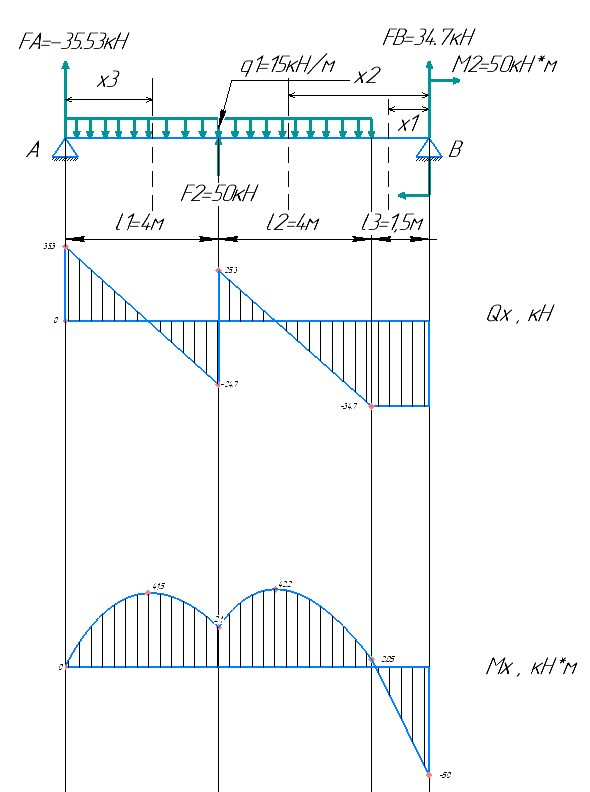   Расчетная схема, эпюры напряжений и моментов для балки, подверженной кручению. Определение размеров поперечного сечения балки при изгибе. 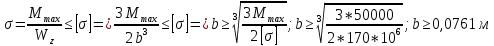 Принимаем b = 77мм, h=154мм Расчет распределения нормальных напряжений по высоте прямоугольного сечения, используя формулу Новье 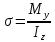 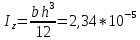 При y=o, σ =0; при y=ymax=h/2=77мм, σ= σmax = 164,52Мпа При y=o, σ =0; при y=ymax=h/2=77мм, σ= σmax = 164,52Мпаσmax< [σ], условие прочности выполняется. Определение размеров двутаврового сечения по условию прочности. 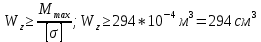 . Wzстанд =371см3, №27 . Wzстанд =371см3, №27 3.4Расчет распределения нормальных напряжений по высоте двутавра, используя формулу Новье 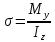 . .При y=0, σ = 0; при y=ymax, σ= σmax=134,7МПа < [σ], условие прочности выполняется. 3.5 Расчет экономии. 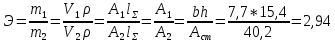 3.6Расчет балки прямоугольного сечения по касательным напряжениям по формуле Журавского 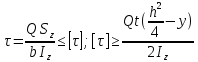 Для точек 1 и 1’: y=h/2, τ1= τ1’=0 Для точки 2 y=0, τ2= τmax = 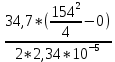 =4,39Мпа =4,39Мпа3.7 Расчет распределения касательных напряжений по высоте двутавра Для точек 1 и 1’ τ1= τ1’=0 Для точек 2 и 2’ τ2= τ2’ = 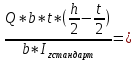 0.898МПа 0.898МПа Для точек 3 и 3’ τ3= τ3’= 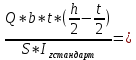 18.7МПа 18.7МПаДля точек 4 и 4’ τ4= τ4’= 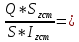 24.6 Мпа 24.6 Мпа3.8Расчет балок на прочность Iучасток 0 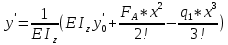 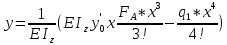 IIучасток 4<x2<8м 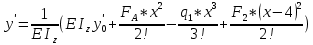 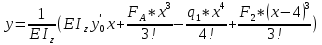 IIIучасток 8<x3<9,5м 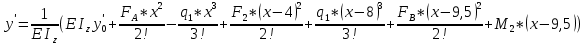 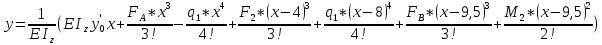 В точке A, то есть при x=9,5, y=0 Определим начальный параметр y’0 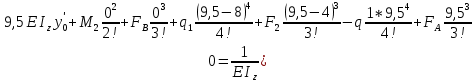 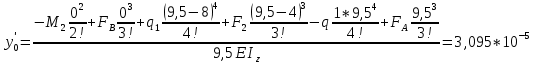 Проверка:2*1011*2,34*10-5*9,5* 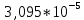 +0+0+1386-5090,66+5077,09=0 +0+0+1386-5090,66+5077,09=0ЗаключениеТаким образом в ходе выполнения данной расчётно-графической работы были определены размеры различных типовых конструкционных элементов при различных условиях, выполнены соответствующие расчёты, оформлены чертежи эпюр к каждой задаче. Для стержня подверженному растяжению-сжатию определены следующие размеры: Для стержня с постоянным сечением по длине: a=16мм Для ступенчатого стержня: a1=14мм, а2=8мм, Коэффициент экономии материала = 1,72 Абсолютное удлинение = 6,87мм, условие жесткости выполняется. Длястержня подверженному кручению определены следующие размеры: Для стержня круглого сечения: d=133мм Для стержня кольцевого сечения: d=190мм Коэффициент экономии материала = 2,57 Суммарный угол закручивания 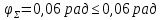 , условие жесткости выполняется. , условие жесткости выполняется.Для балки подверженной изгибу определены следующие размеры: Для балки прямоугольного сечения: b=77мм, h=154мм Для двутавровой балки: по ГОСТ 8239-89 №27 Коэффициент экономии материала = 2,94 Список использованной литературыОпределение внутренних силовых факторов в поперечных сечениях стержней: Методические указания к выполнению расчётно-графической работы по курсу «Сопротивление материалов». /к.техн.н, доцент Бартенев, Д.А;д.техн.н., проф. Марцулевич, Н.А.; ст.преп. Сташевская, О.В. – СПб.: Изд-во СПбГУЭФ, 2004. – 60с. |
