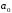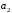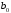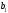РГЗ ПО ЦОС (2) (2). Расчетно графическая работа по цифровая обработка сигнала
 Скачать 443.16 Kb.
|
  МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И ФИЗИКИ Кафедра РП и РПУ Расчетно графическая работа по цифровая обработка сигнала Вариант: 44
Новосибирск – 2021 г. Задание №1. По разностному уравнению 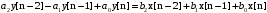 Требуется: 1. Записать передаточную функцию цепи в виде частного двух полиномов. 2. Найти корни числителя и знаменателя. 3. Построить нуль-полюсную диаграмму, обозначить область сходимости z-преобразования импульсной характеристики. 4. Определить, какая цепь (каузальная, антикаузальная, некаузальная) является устойчивой. 5. Составить структурную схему устойчивой цепи в прямой форме. 6. Рассчитать АЧХ и ФЧХ цепи, построить графики. 7. Построить сигнальный граф цепи в прямой и канонической форме. 8. Построить графы для каскадной и параллельной форм реализации цепи. 9. Записать передаточные функции, соответствующие каскадной и параллельной формам реализации. 10. Определить аналитически импульсную характеристику цепи. 11. Построить график импульсной характеристики .
Выразим y[n] с нормированием по a0 : 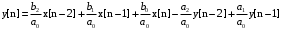 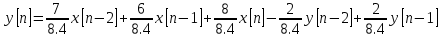 В итоге получим:  Для построения нуль-полюсной диаграммы и определения области сходимости записываем передаточную функцию цепи H(z) в виде частного двух полиномов: 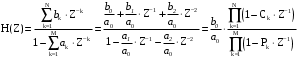 ;Где N – число нулей переда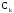точной функции (  ), M – число полюсов передаточной функции (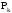 ).Рассчитаем корни числителя и знаменателя.  Корни числителя – это нули передаточной функции: 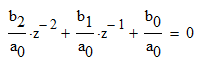    Корни знаменателя — это полюса передаточной функции:    Строим нуль-полюсную диаграмму, содержащую нули и полюса. 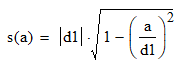 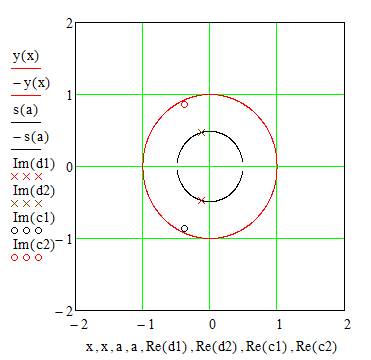  Рисунок 1.1 – Нуль-полюсная диаграмма По нуль-полюсной диаграмме видно, что цепь устойчива, так как область сходимости включает единичную окружность. Так как 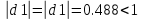 то для того, чтобы цепь была устойчивой область сходимости должна быть внешность круга, следовательно последовательность правосторонняя. По полученным данным составим схему Выразим y[n] с нормированием по a0 : 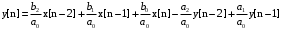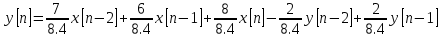В итоге получим:  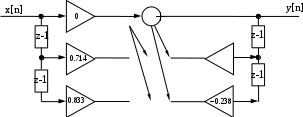Рисунок 1.2 – Схема цепи в прямой форме Для построения АЧХ и ФЧХ требуется преобразование передаточной функции заменой z на e-jω: 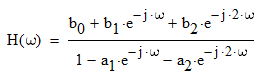  Построим графики АЧХ и ФЧХ в диапазоне [-π;π] 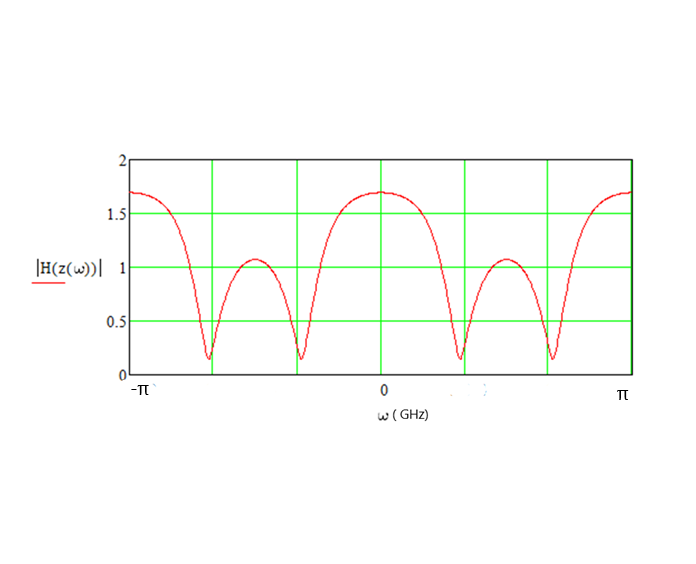 πРисунок 1.3 – АЧХ фильтра 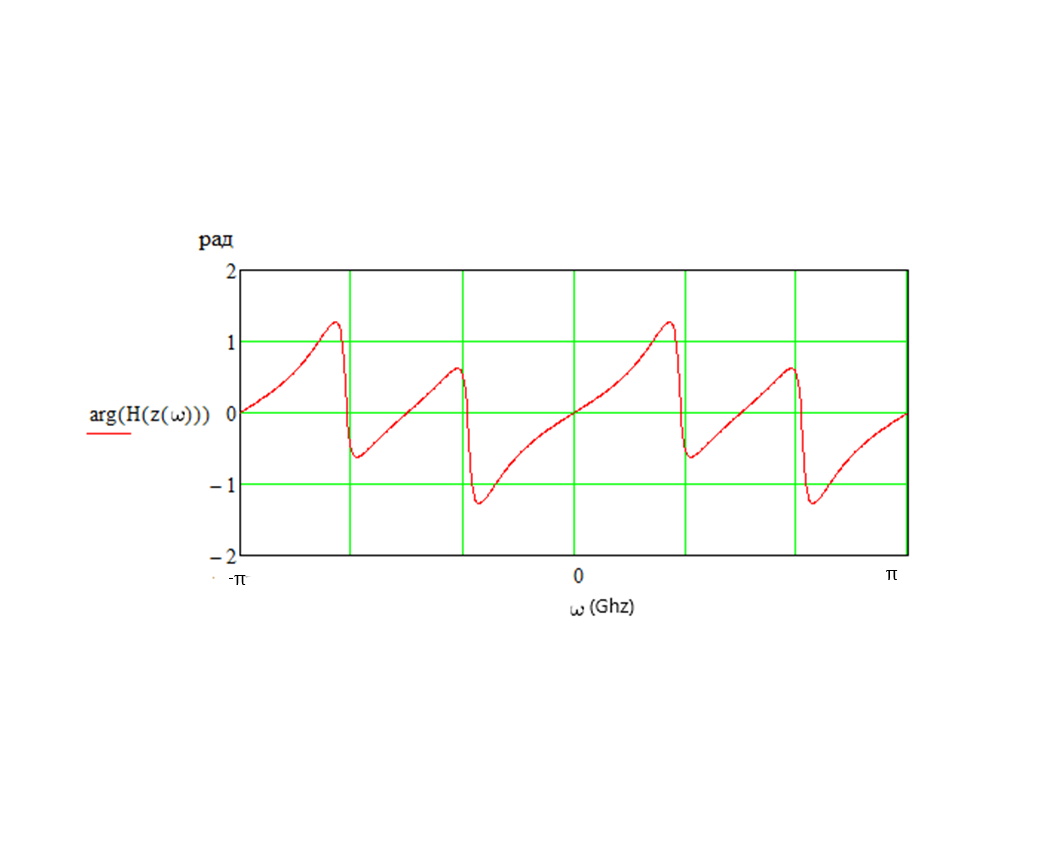 Рисунок 1.4 – ФЧХ фильтра Построим сигнальный граф в прямой форме. 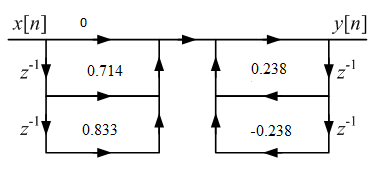 Рисунок 1.5 – Сигнальный граф в прямой форме Построим графы для каскадной и параллельной форм реализации цепи. Так как степени числителя и знаменателя равны, то сигнальный граф необходимо дополнить трансверсальной цепью первого порядка:  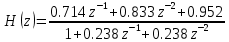Разложим правильную дробь на сумму двух: 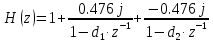 Для построения сигнального графа в каскадной форме необходимо передаточную функцию представить в виде произведения простых сомножителей: 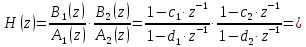 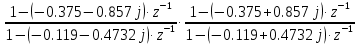 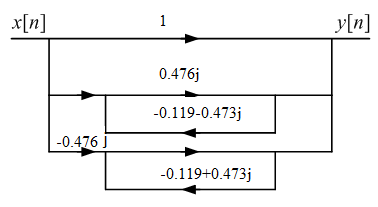 Рисунок 1.6 – Сигнальный граф цепи в параллельной форме  Рисунок 1.7 – Сигнальный граф цепи в каскадной форме Для определения импульсной характеристики применим к передаточное функции обратное z-преобразование 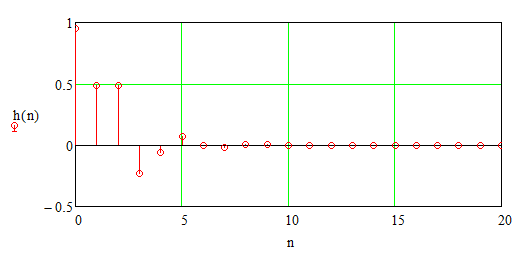  Рисунок 1.8 – Импульсная характеристика каузальной цепи Задание 2По заданному набору нулей требуется: 1. Записать передаточную функцию цепи. 2. Рассчитать АЧХ и ФЧХ, построить графики. 3. Записать разностное уравнение цепи. 4. Определить импульсную характеристику, построить график. 5. Изобразить структурную схему в прямой форме. 6. Построить сигнальный граф цепи в прямой и каскадной форме. 7. Представить цепь каскадным соединением минимально-фазовой и всепропускающей цепей. 8. Определить АЧХ и ФЧХ этих цепей, построить их графики. 9. Записать разностные уравнения МФЦ и ВПЦ, определить их импульсные характеристики, построить графики. Исходные данные для расчета:
Записываем передаточную функцию цепи в виде сомножителей:π 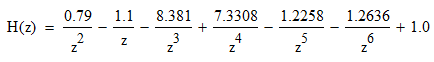  Для построения АЧХ и ФЧХ запишем комплексную передаточную характеристику H(ω), сделав замену z на e-jω: 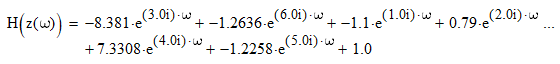 Построим АЧХ и ФЧХ в диапазоне [-π;π]  Рисунок 2.1 – АЧХ цепи 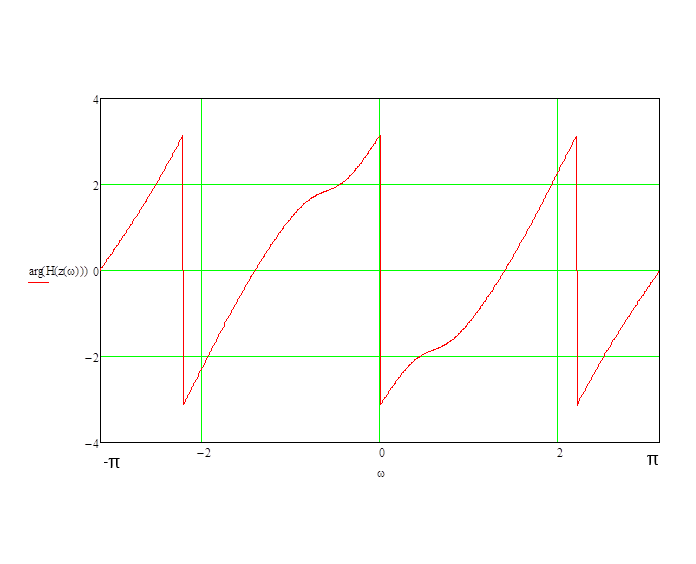 Рисунок 2.2 – ФЧХ цепи Запишем разностное уравнение цепи: 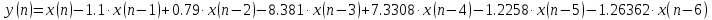 Так как цепь нерекурсивная, то она обладает конечной импульсной характеристикой. В этом случае импульсная характеристика равная коэффициентам при х: 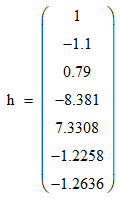 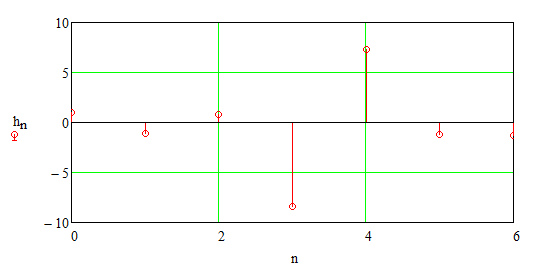 Рисунок 2.3 – Импульсная характеристика цепи 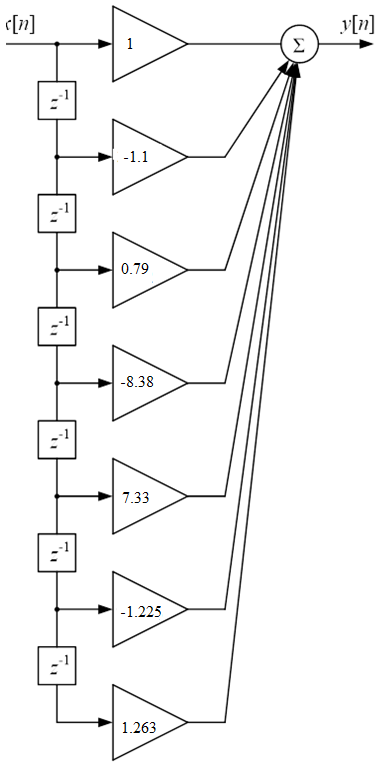 Рисунок 2.4 – Структурная схема цепи в прямой форме. Построим сигнальный граф цепи в прямой и каскадной форме, для нерекурсивной цепи они совпадают. 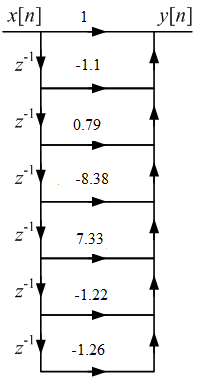 Рисунок 2.5 – Сигнальный граф в прямой форме Представим цепь каскадным соединением минимально-фазовой и всепропускающей цепей. Для всепропускающей цепи должно выполняться связь между нулями и полюсами: 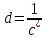 Для минимально-фазовой цепи должно выполняться условие, что все нули лежат внутри единичной окружности. Под это условие подходят c1, c2 и c3. Для остальных нулей рассчитаем парные значения полюсов: 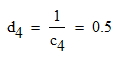 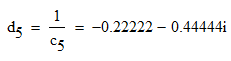 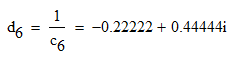 Тогда передаточная функция минимально-фазовой цепи:  Передаточная функция всепропускающей цепи: 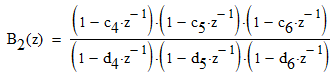 При этом видно, что выполняется условие: 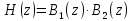 Для определения АЧХ и ФЧХ цепей выполним замену z на e-jω в выражениях для B1(z) и B2(z). 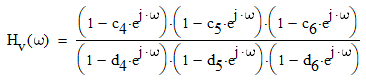  Построим АЧХ и ФЧХ в диапазоне частот [–π; π]. 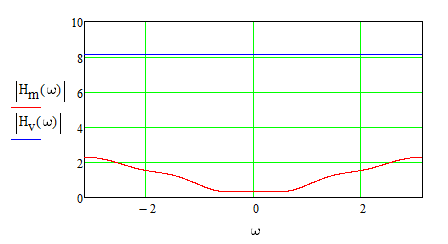 Рисунок 2.6 – АЧХ минимально-фазовой и всепропускающей цепей  Рисунок 2.7 – ФЧХ минимально-фазовой и всепропускающей цепей Чтобы записать разностные уравнения МФЦ и ВПЦ, преобразуем выражения для B1(z) и B2(z). 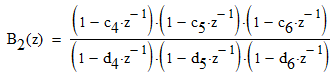 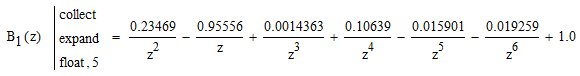 Разностное уравнение МФЦ: 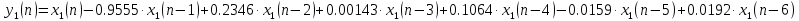 Импульсная характеристика для МФЦ: 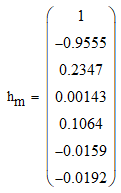  Рисунок 2.8 – Импульсная характеристика для МФЦ Рассчитаем импульсную характеристику для ВПЦ. 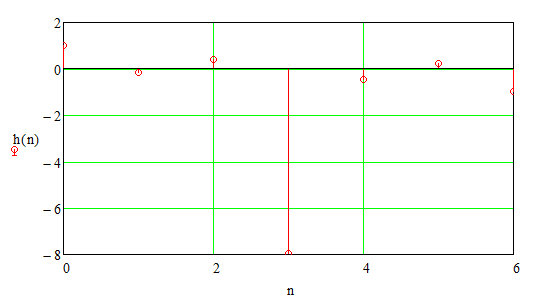  Рисунок 2.9 – Импульсная характеристика для ВПЦ Импульсная характеристика ВПЦ затухает, цепь устойчива. Список литературы Васюков В.Н. Цифровая обработка сигналов и сигнальные процессоры в системах подвижной радиосвязи. – Новосибирск: Изд-во НГТУ, 2005. – 392 с. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов: Пер. с англ. – М.: Техносфера, 2012. – 1048 с. Лайонс Р. Цифровая обработка сигналов. М.: ООО «Бином-Пресс», 2006. – 656 с.
|
