Расчетно-графическое Задание N1_2020. Расчетнографические задания по общей физике. 1
 Скачать 4.92 Mb. Скачать 4.92 Mb.
|
|
17. Действие электрического и магнитного полей на движущиеся заряды Пример 17.1. Найти траекторию движения электрона в однородном магнитном поле, если Математическая модель где 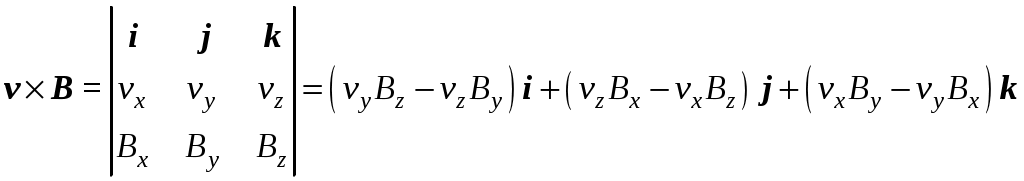 . (2) . (2)Решение Подставляя начальные значения в (2) получаем уравнение движения для электрона В декартовых координатах уравнение движения (3) может быть представлено в виде системы уравнений 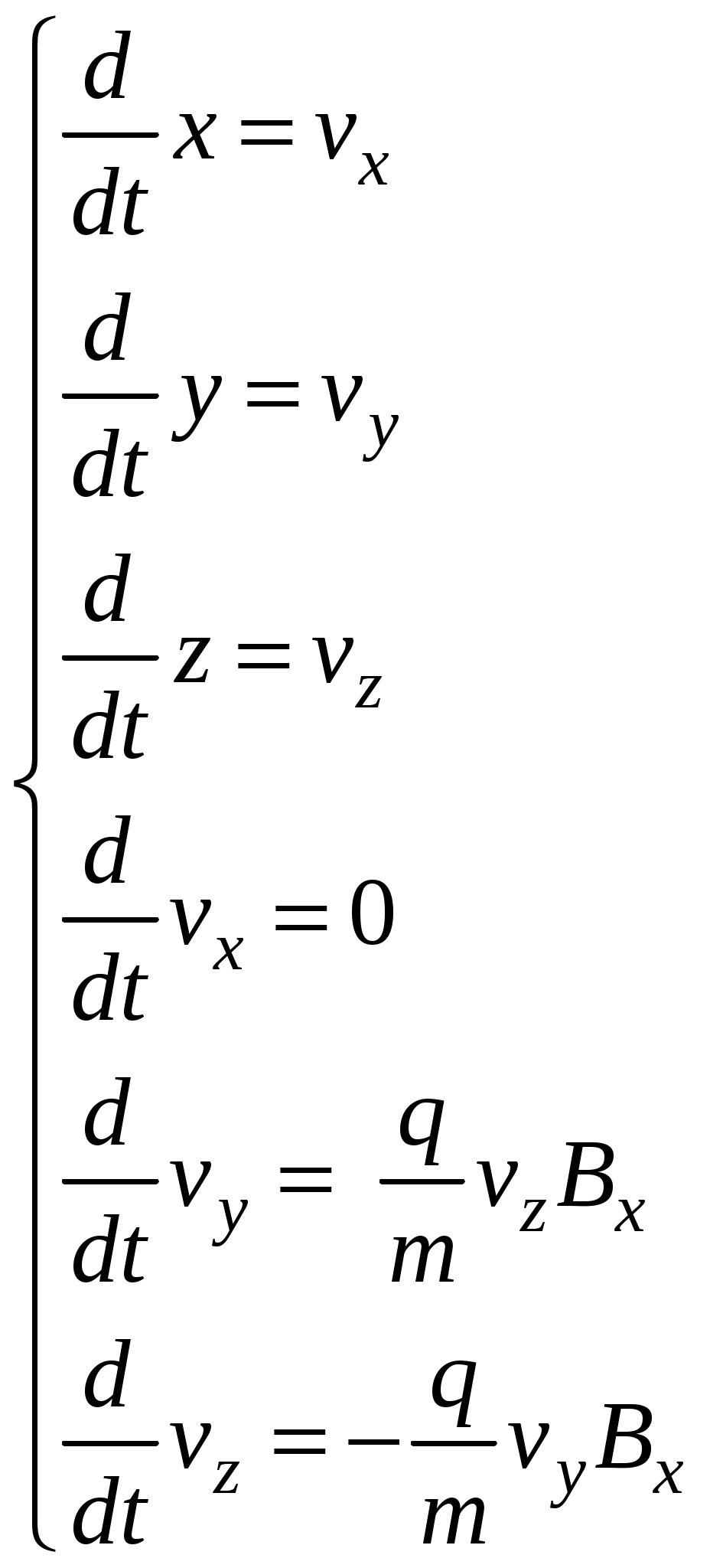 (4) (4)Эта задача допускает аналитическое решение, электрон движется по винтовой линии радиуса 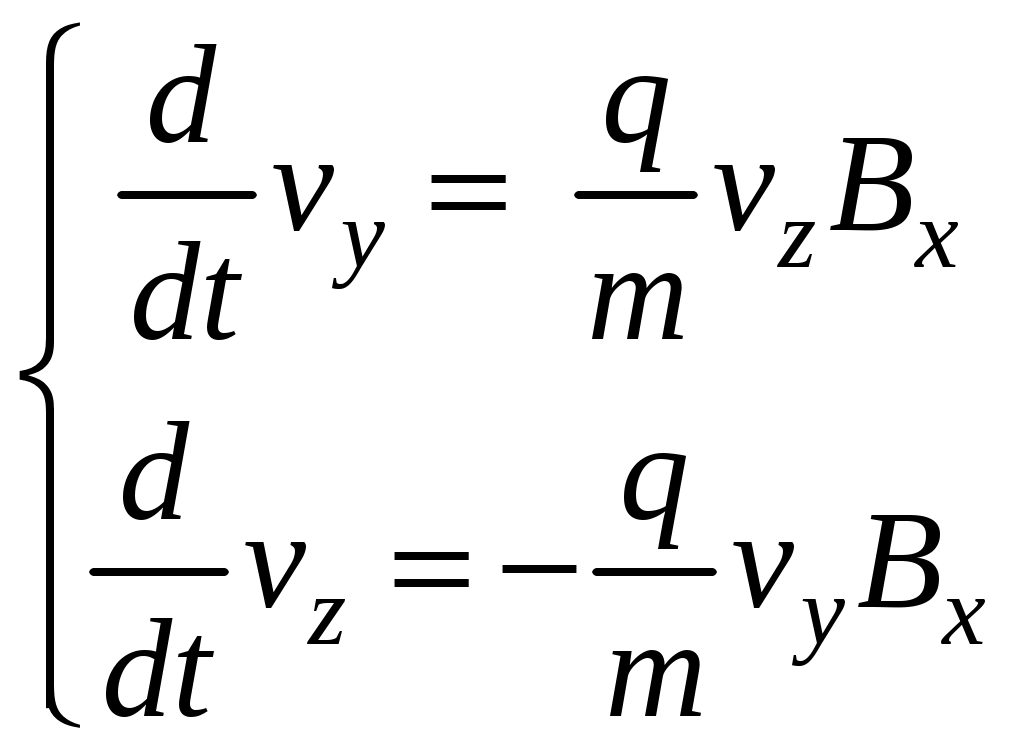 (5) (5)Переходя к переменной 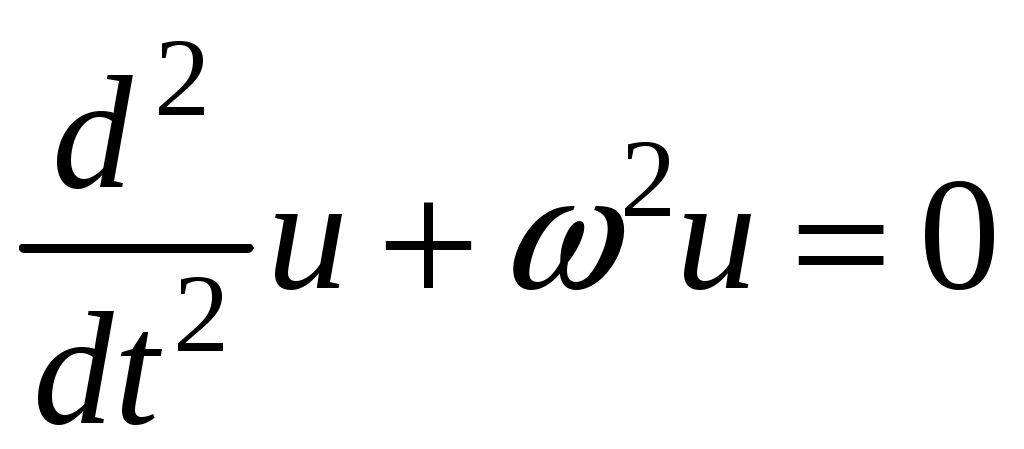 (6) (6)где соответственно, 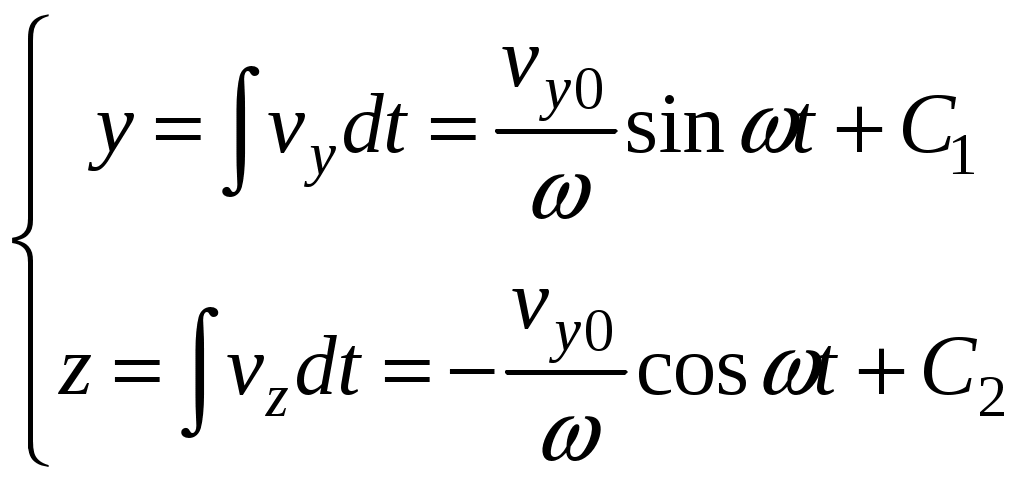 (8) (8)Применяя начальные условия к (8), получаем Таким образом, ось винтовой линии параллельна оси Для графического представления траектории движения иногда проще рассчитать и построить сложную пространственную кривую, чем делать график при помощи чертежных приспособлений. Для этого в составе всех универсальных математических пакетов имеется графический инструментарий. Здесь приведен рабочий документ пакета Maple, в котором приведен код расчета траектории электрона > > > > > 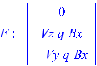 > > > > 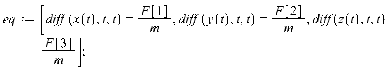 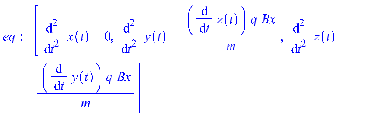 > 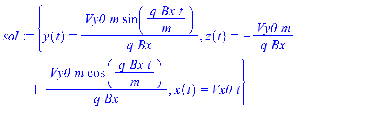 > > > 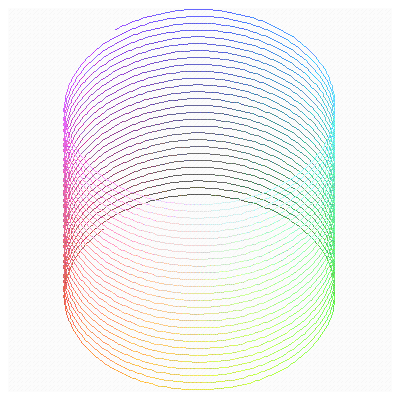 > Ответ: *** 17.1. Электрон, обладающий энергией 1000 эВ, влетает в однородное электрическое поле E= 800 В/см, перпендикулярно силовым линиям поля. Каковы должны направление и величина магнитного поля B, чтобы электрон не испытывал отклонений? Построить траекторию движения электрона. 1 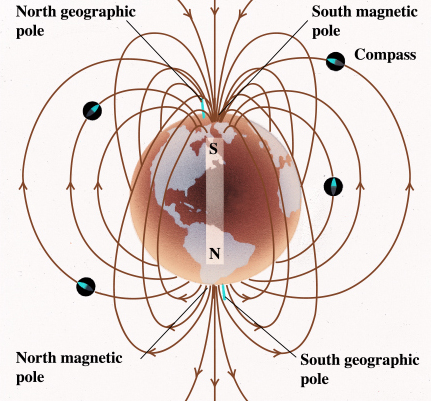 7.2. Электрон, ускоренный напряжением 200 В, движется в магнитном поле Земли со скоростью, которая перпендикулярна линиям магнитной индукции B. Радиус окружности движения электрона 0,68 м. Найти индукцию магнитного поля Земли. Построить траекторию движения электрона. 7.2. Электрон, ускоренный напряжением 200 В, движется в магнитном поле Земли со скоростью, которая перпендикулярна линиям магнитной индукции B. Радиус окружности движения электрона 0,68 м. Найти индукцию магнитного поля Земли. Построить траекторию движения электрона.17.3. Протон, ускоренный разностью потенциалов 250 кВ, пролетает поперечное однородное магнитное поле с индукцией 0.1 Тл. Толщина области 5 см. Построить траекторию протона и найти угол отклонения от первоначального направления движения. 1 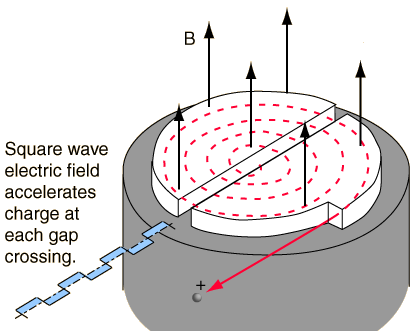 7.4. Точечный заряд 10 мКл влетает со скоростью 5 м/с в однородное магнитное поле. Вектор скорости заряда и вектор магнитной индукции поля взаимно перпендикулярны. Найдите величину и направление силы, действующей на заряд. Индукция магнитного поля 2 Тл. Построить траекторию движения заряда. 7.4. Точечный заряд 10 мКл влетает со скоростью 5 м/с в однородное магнитное поле. Вектор скорости заряда и вектор магнитной индукции поля взаимно перпендикулярны. Найдите величину и направление силы, действующей на заряд. Индукция магнитного поля 2 Тл. Построить траекторию движения заряда.17.5. Между дуантами циклотрона приложено напряжение 40 кВ. Индукция магнитного поля, заставляющего двигаться частицы двигаться по окружности равна 0,8 Тл. Определить разность радиусов траекторий протона после 4-го и 9-го прохождения щели. Построить траекторию движения заряда. 17.6. Циклотрон предназначен для ускорения протонов до энергии 8 10-13 Дж. Определить наибольший радиус орбиты, по которой движется протон, если индукция магнитного поля равна 1 Тл. Построить траекторию движения протона. 17.7. Протоны ускоряются в циклотроне так, что максимальный радиус орбиты R =2 м, Частота генератора циклотрона 1  7.8. Между дуантами циклотрона приложено напряжение 30 кВ. Индукция магнитного поля, заставляющего двигаться частицы двигаться по окружности равна 0,8 Тл. Определить разность радиусов траекторий протона после 5-го и 10-го прохождения щели. Построить траекторию движения заряда. 7.8. Между дуантами циклотрона приложено напряжение 30 кВ. Индукция магнитного поля, заставляющего двигаться частицы двигаться по окружности равна 0,8 Тл. Определить разность радиусов траекторий протона после 5-го и 10-го прохождения щели. Построить траекторию движения заряда.17.9. Электрон влетает в пространство, где на него действуют два взаимно перпендикулярных магнитных поля с магнитными индукциями 1,73 мТл и 2,30 мТл. Начальная скорость электрона 17.10. Электрон влетел в однородное электрическое поле, напряженность которого изменяется по гармоническому закону амплитудой 100 В/см и частотой 1 МГц. Начальная скорость частицы направлена перпендикулярно направлению силовых линий поля. Определить уравнение траектории частицы и длину пути, если электрон обладал начальной кинетической энергией 10 эВ и толщина области поля составляет 10 см. Построить траекторию движения электрона. 18. Колебания Пример 18.1. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты где Решение Построим график потенциальной энергии, для уточнения вида кривой найдем точки экстремума 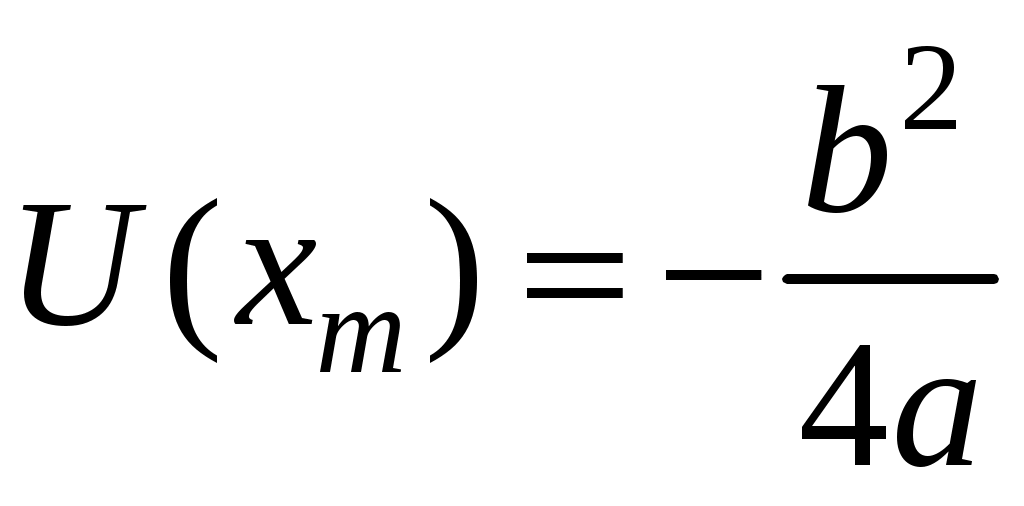 . .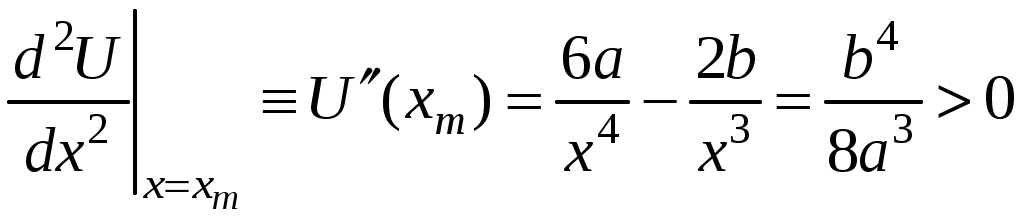 Таким образом, вычисленная точка определяет минимум потенциальной энергии, построим график Разложим 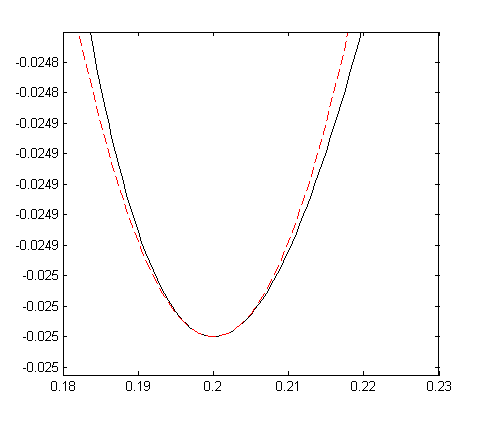 Рис.18.1. Потенциальная энергия частицы: Найдем уравнение движения маятника, для этого запишем уравнение Ньютона 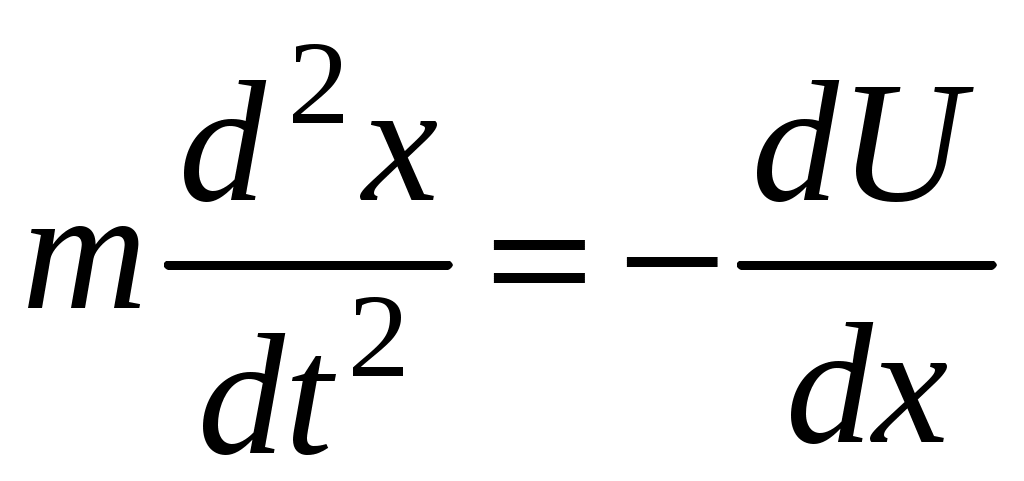 или или 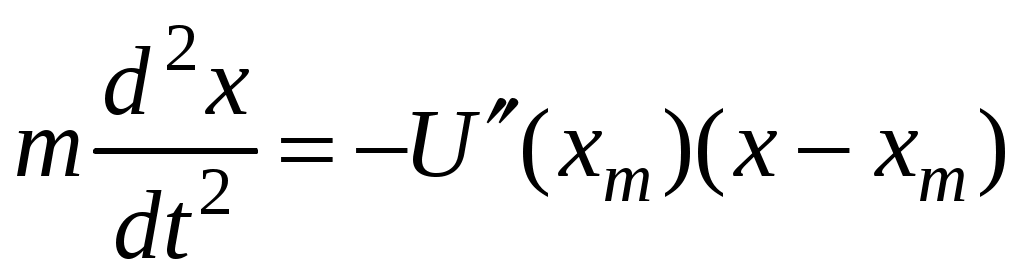 Перейдем к переменной 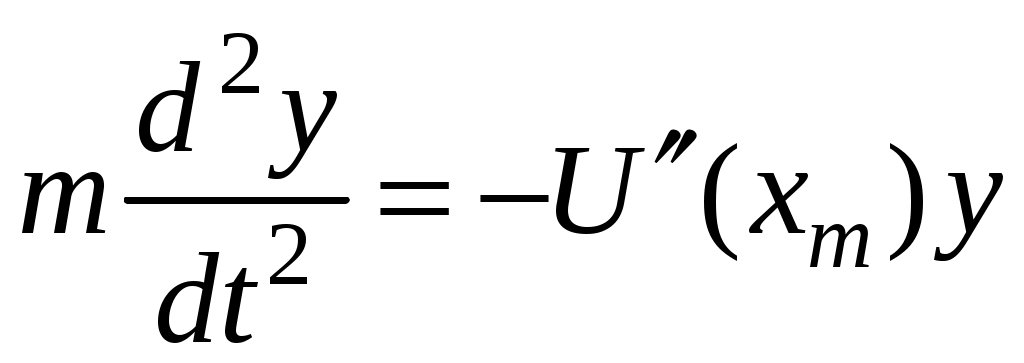 или или 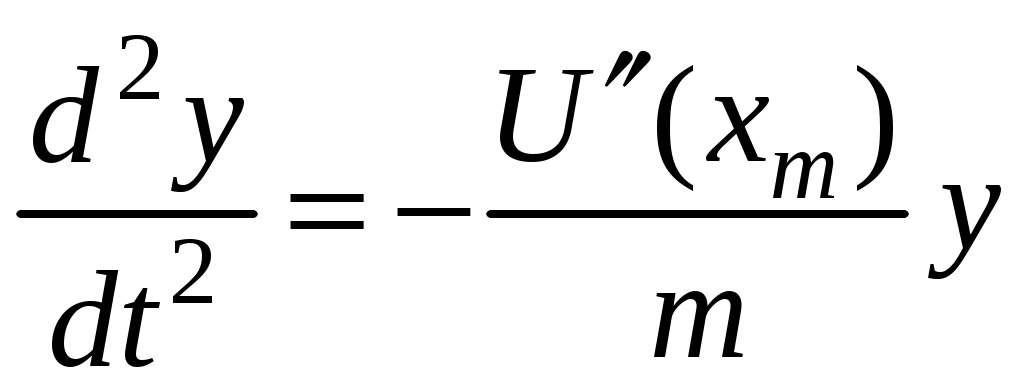 Тогда частота малых колебаний равна 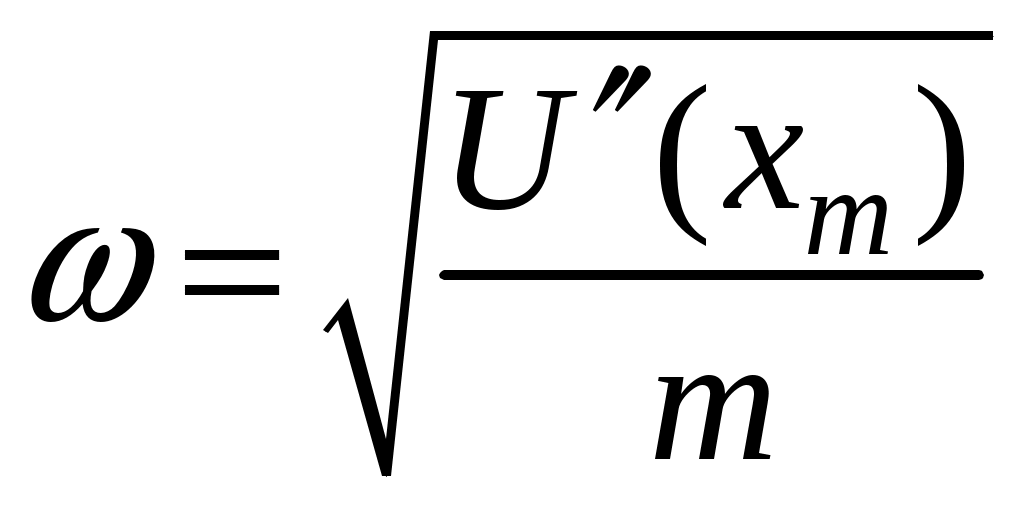 или или 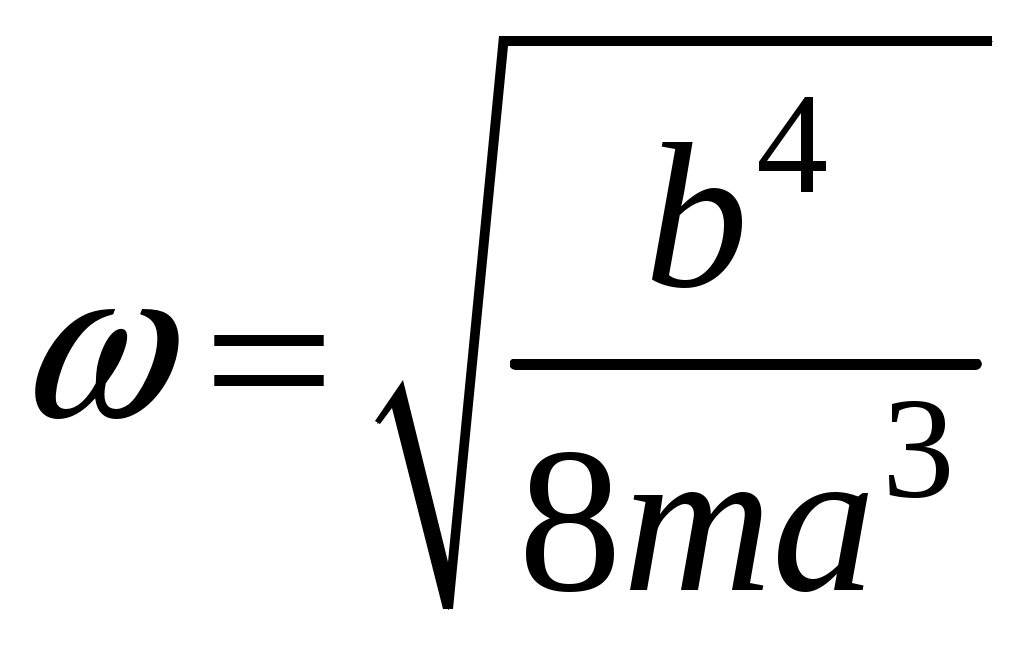 , , а период малых колебаний равен Чтобы построить график зависимости Тогда колебания тела описываются такой системой уравнений 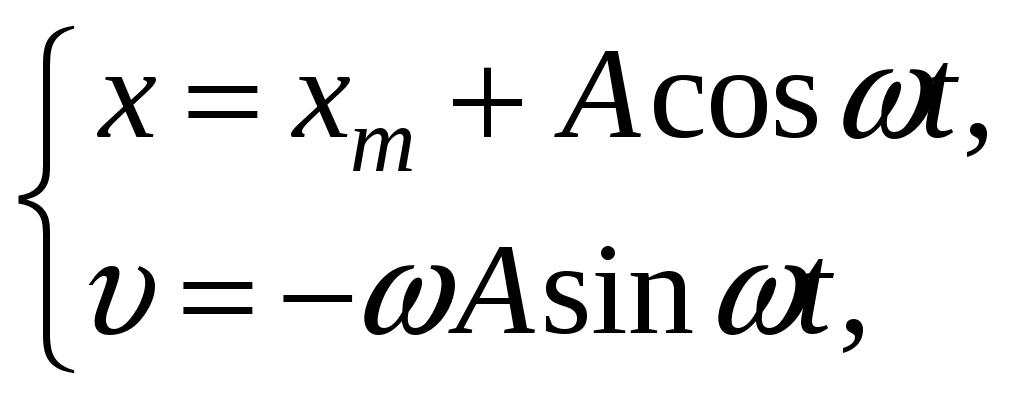 где Составим программу (Python). # Фазовая траектория частицы import math as mt import matplotlib.pyplot as plt a=0.001; b=0.01; m=0.2; x1=0.21; xm=2.*a/b; A=x1-xm; w=mt.sqrt(b**4/(8.*m*a**3)); T=2.*mt.pi/w; tmin=0.0; tmax=2.*T; NT=500; dt=(tmax-tmin)/NT; ti=[]; X=[]; V=[]; ti.append(tmin); X.append(x1); V.append(0.); for i in range(NT): t1=tmin+i*dt;ti.append(t1); X.append(xm+A*mt.cos(w*t1)); V.append(A*w*mt.sin(w*t1)); plt.plot(X,V,'k-') plt.grid(True) plt.xlabel('$x$',fontsize=16) plt.ylabel('$v$',fontsize=16) plt.show() По результатам расчета построим фазовый портрет движения тела 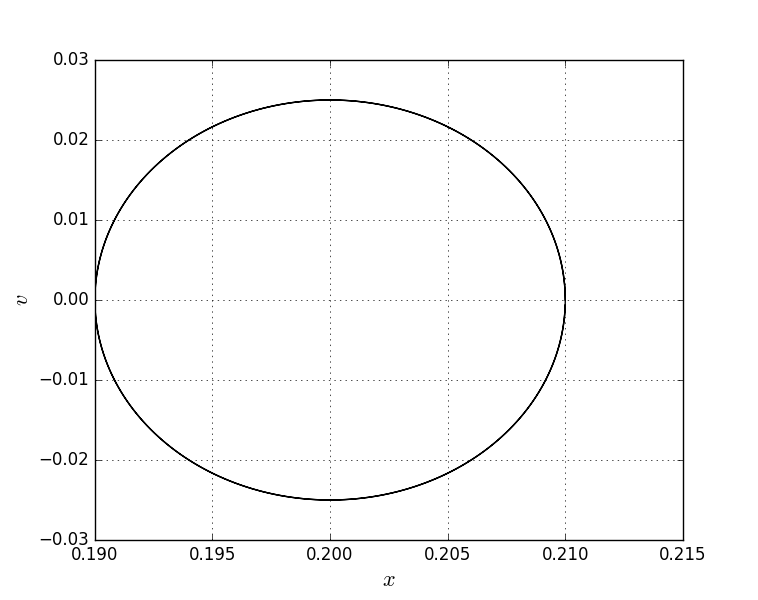 Рис.18.2. Фазовый портрет движения частицы. В начальный момент времени тело находится в крайнем правом положении, затем начинает смещаться влево по часовой стрелке по эллиптической траектории, как показано на рис.6.2, делая полный оборот за 2.51 с. Ответ: *** 18.1. Тело совершает колебания по закону 18.2. Тело совершает колебания по закону 18.3. Однородный диск массы 3 кг и радиуса 20 см скреплен в центре диска с тонким стержнем так, что стержень перпендикулярен плоскости диска. Другой конец стержня закреплен жестко и неподвижно. Коэффициент кручения стержня (отношение приложенного вращающего момента к углу закручивания) равен 6.00 Н·м/рад. Определить: а) частоту малых крутильных колебаний; б) амплитуду и начальную фазу колебаний, если в начальный момент времени угол 18.4. Материальная точка совершает колебания по закону синуса с амплитудой 10 см, частотой 2 Гц и начальной фазой 30 градусов. Полная энергия колеблющейся точки 0.077 Дж. Через какой промежуток времени от начала движения кинетическая энергия станет равной потенциальной? Построить график зависимости 18.5. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 18.6. Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0 с частотой 4.00 с-1. В некоторый момент времени координата частицы равна 25 см и ее скорость 100 см/с. Найти координату и скорость частицы через 2.4 с после этого момента времени. Построить график зависимости 18.7. Определите амплитуду гармонических колебаний материальной точки, если полная энергия колеблющейся точки 0.04 Дж, а максимальная сила, действующая на точку, равна 2 Н. Привести поясняющий рисунок и указать основные параметры 18.8. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты 18.9. На доске лежит груз массой 10 кг. Доска совершает гармонические колебания по закону косинуса в вертикальном направлении с периодом 0.5 с и амплитудой 2 см. Определите величину давления 18.10. Найти период малых поперечных колебаний шарика массы 40 г, укрепленного на середине натянутой струны длины 1 м. Силу натяжения струны считать постоянной и равной 10 Н. Массой струны и силами тяжести пренебречь. Построить график зависимости 18.11. Уравнение изменения силы тока в колебательном контуре дано в виде 18.12. Колебательный контур имеет индуктивность 0.23 Гн, емкость конденсатора 7 мкФ. Сопротивление контура 40 Ом. Конденсатор заряжен 0.56 мКл. Найдите: а) период колебаний, б) логарифмический декремент затухания колебаний λ. Напишите уравнение зависимости разности потенциалов на обкладках конденсатора от времени. Построить векторную диаграмму напряжений и привести графики 18.13. Заряженный конденсатор емкостью 0.35 мкФ подключили к катушке индуктивностью 0.25 мГн. Через какое время после подключения катушки энергия электрического поля станет равной энергии магнитного поля катушки? Построить графики энергий. Активным сопротивлением контура пренебречь. 18.14. В колебательном контуре, состоящем из конденсатора и катушки индуктивностью 2.5 мГн, происходят электромагнитные колебания, при которых максимальная сила тока 10 мА. Определить емкость конденсатора, если максимальная разность потенциалов на его обкладках достигает 50 В, а активным сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики 18.15. Определить частоту собственных колебаний колебательного контура, который состоит из конденсатора емкостью 2 мкФ и катушки длиной 10 см и радиусом 1 см, содержащим 500 витков. Учесть, что происходят электромагнитные колебания, при которых максимальная сила тока в контуре 10 мА. Сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики 18.16. Колебательный контур имеет индуктивность 1.6 мГн, емкость конденсатора 0.04 мкФ и максимальную разность потенциалов на обкладках конденсатора 200 В. Чему равна максимальная сила тока в контуре? Активное сопротивление контура мало. Построить векторную диаграмму напряжений и привести графики |
