Расчетно-графическое Задание N1_2020. Расчетнографические задания по общей физике. 1
 Скачать 4.92 Mb.
|
|
19.Затухающие колебания Пример 19.1. Горизонтальное колебательное движение бруска при наличии сухого трения. Пружинный маятник представляет собой брусок массой  , лежащий на горизонтальной плоскости, соединенный горизонтальной пружиной с вертикальной стенкой. Брусок в начальный момент времени сместили из положения равновесия  на  , так что пружина растянулась, затем отпустили с нулевой скоростью. Сколько колебаний совершит брусок до момента остановки, если коэффициент сухого трения скольжения равен  ?Для численных расчетов принять  кг,  Н/м,  ,  м.Математическая модель 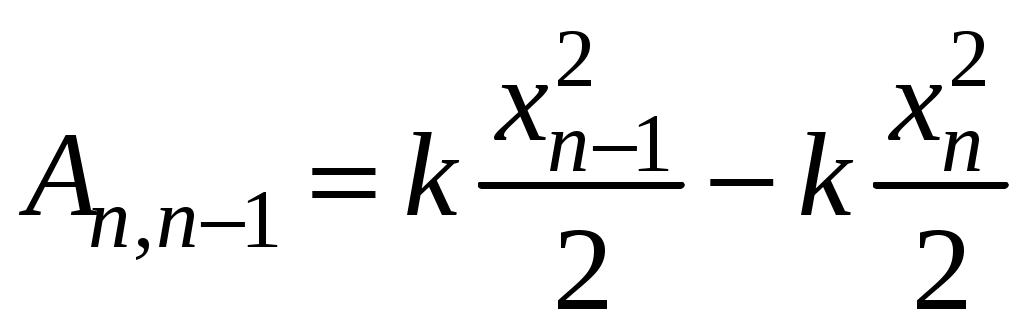 (19.1) (19.2) (19.3)Знак минус в (19.2) связан с тем, что сила трения направлена против смещения бруска,  координаты точек остановки на полупериоде. Решение Процесс движения бруска показан на рис.1 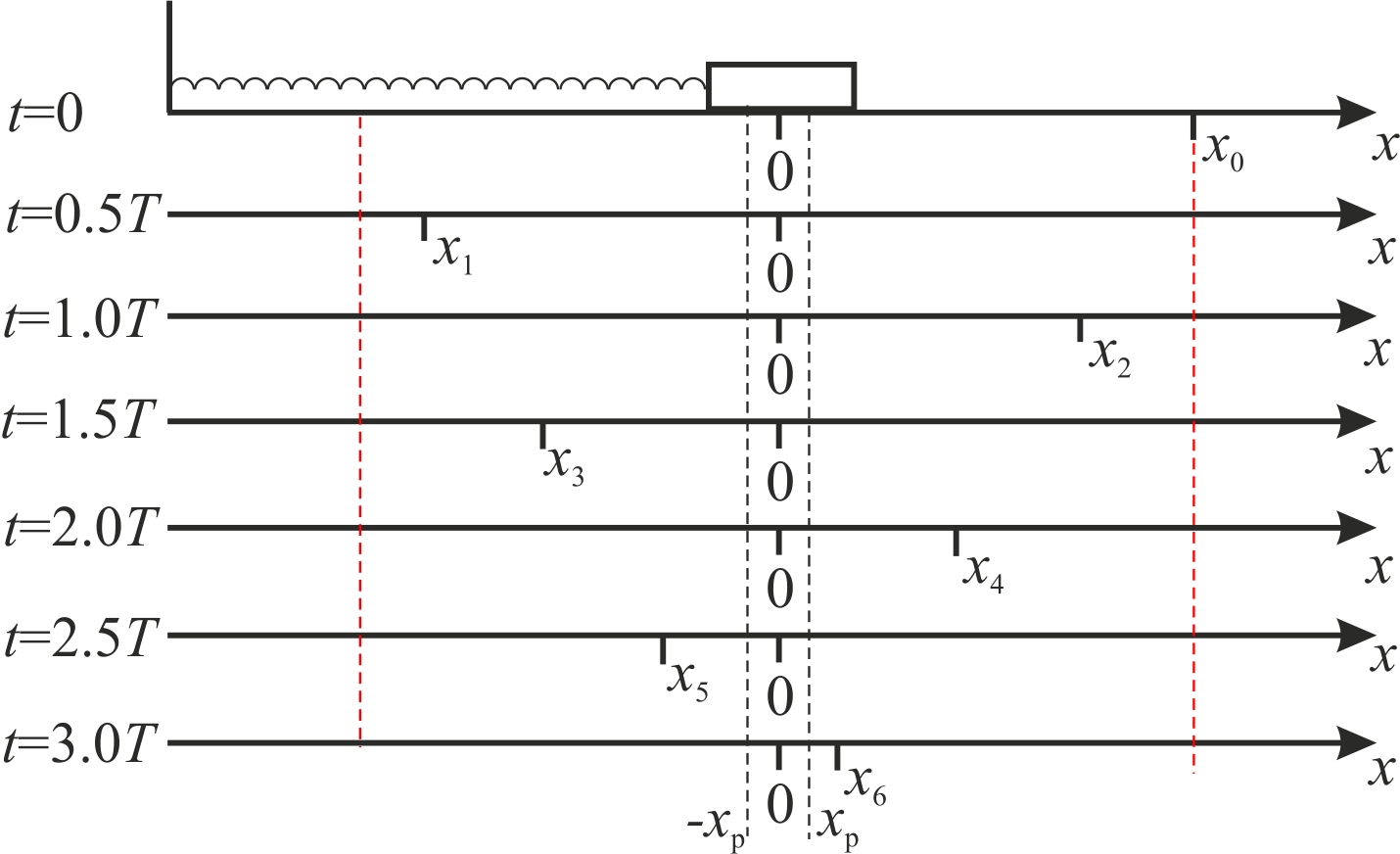 Рис.19.1. Координатно-временная развертка крайних положений бруска Решение Из (19.2) и (19.3) следует 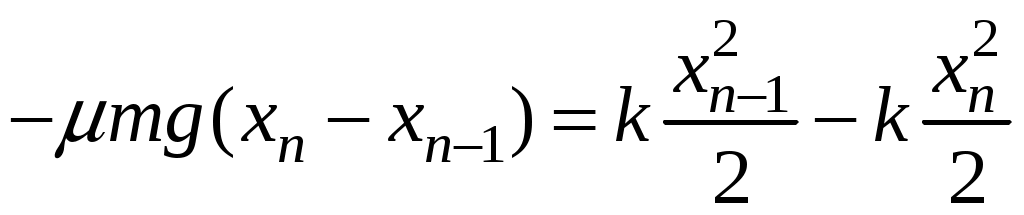 (19.4)Определим область застоя  , в которой сила упругости в точности компенсируется силой трения покоя , (19.5)Из (19.4) координаты крайних точек остановки равны  . (19..6)Колебания продолжаются до тех пор, пока 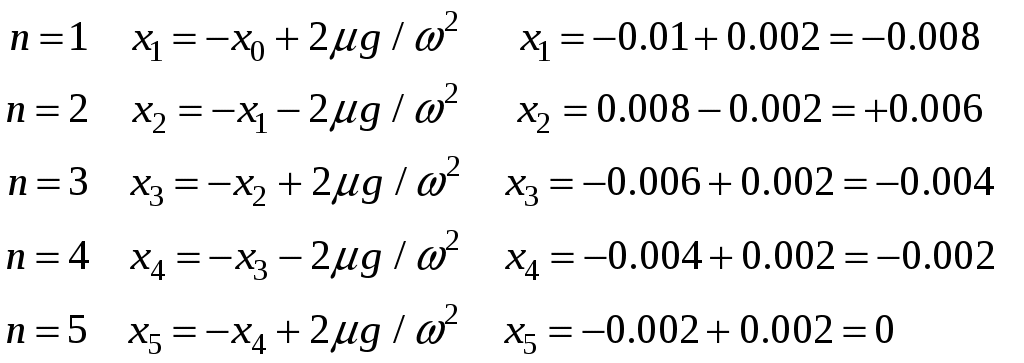 не попадет в область застоя, а именно для данных численных параметров получаем: Время движения равно  с.Для проверки проделаем численный расчет движения бруска на основе модели (19.1), проектируем на горизонтальную ось, получаем уравнение движения Движение справа — налево  (19.7)Движение слева — налево  (19.8)На рис.19.2 представлен результат численного расчета данной модели (текст программы приведен в Приложении) 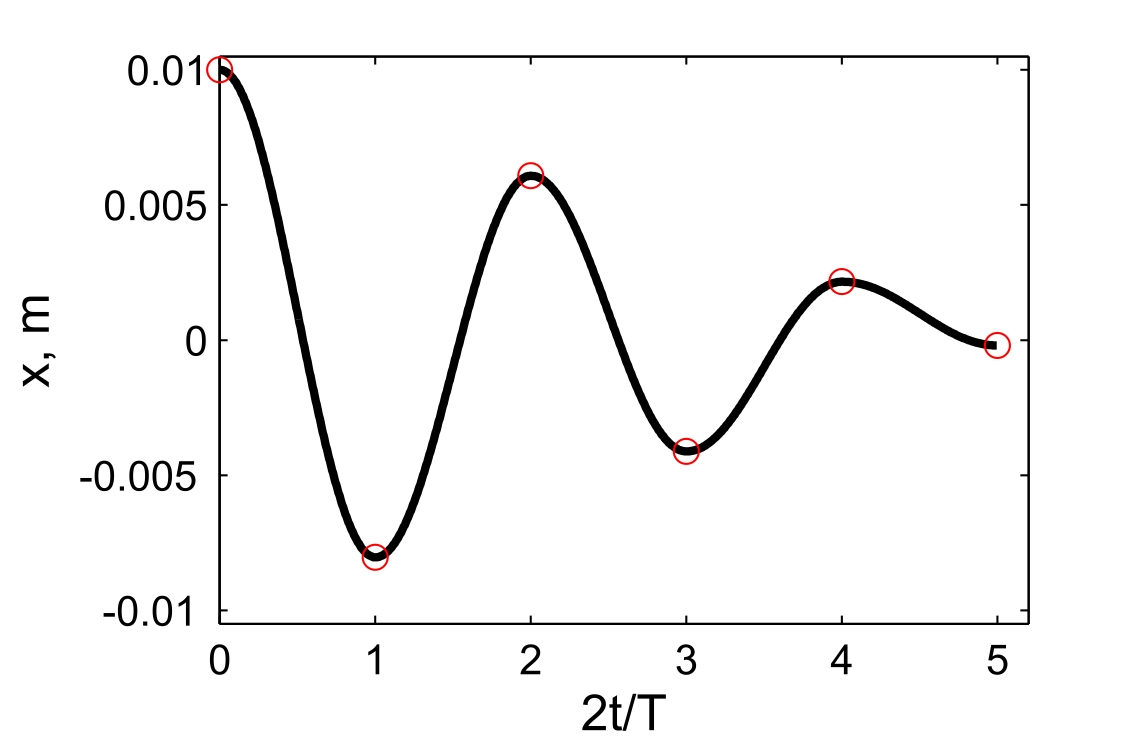 Рис. 19.2. График колебаний бруска, рассчитанный по модели (19.7), (19.8). Кружки отмечают крайние положения бруска, рассчитанные по формуле (19.6)Несмотря на совпадения крайних положений бруска с положениями бруска, рассчитанными по модели (7.7) и (7.8), мы получили правдоподобный результат, поскольку в решении мы не учли область застоя около положения равновесия. График скорректированного решения приведен на рис.19.3. 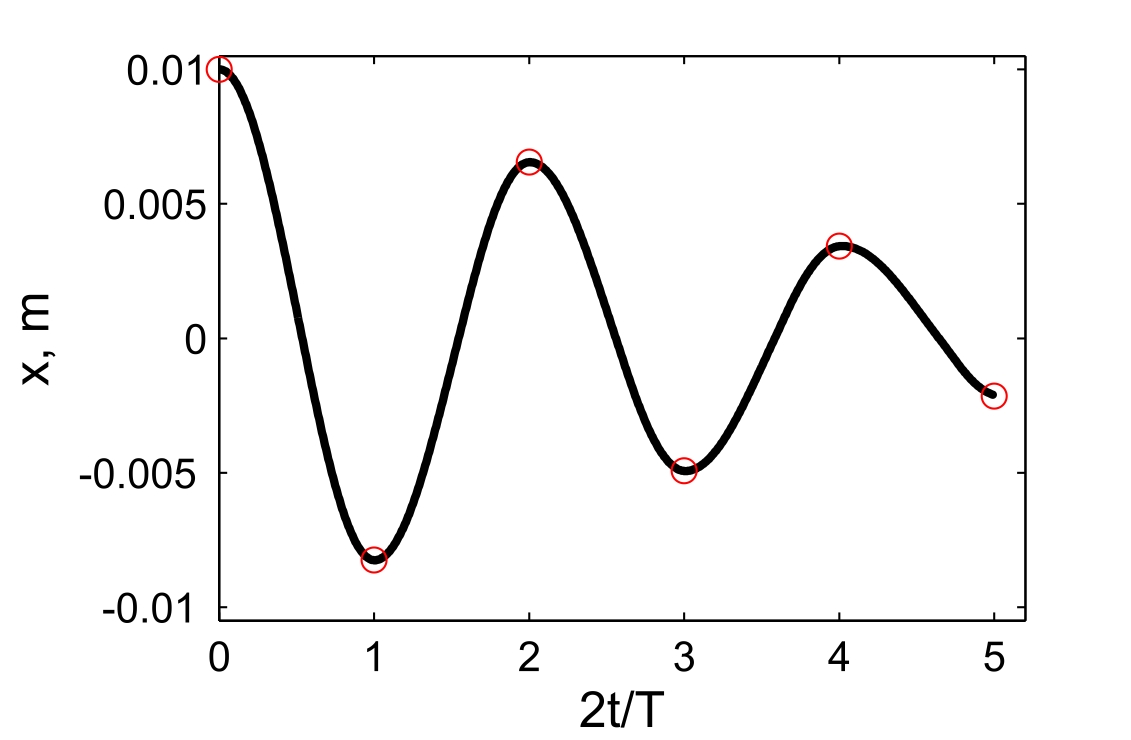 Рис. 19.3. График колебаний бруска, рассчитанный по модели (19.7), (19.8) с учетом области застоя. Кружки отмечают скорректированные крайние положения бруска.Таким образом, колебания бруска затухают слабее, поскольку в области застоя брусок движется равномерно. Получается парадокс, шероховатость горизонтальной плоскости везде одинакова, а в области застоя работу силы трения не учитываем. Ответ: Маятник совершил 2.25 колебания в течение 1.57 секунд. 19.1. Груз массой 0.5 кг подвешен к пружине, жесткость которой 32 Н/м, и совершает затухающие колебания. Определите период затухающих колебаний, если за время двух колебаний амплитуда уменьшилась в 3 раза. Построить график зависимости  .19.2. Маятник длиной l = 5 м совершает малые колебания, так что амплитуда их уменьшилась в два раза за 100 периодов. Найдите добротность Q колебаний, логарифмический декремент λ и коэффициент затухания  . Построить график зависимости .19.3. Затухающие колебания частицы были возбуждены путем ее смещения из положения равновесия на расстояние 1 см. Логарифмический декремент затухания 0.0100. При столь слабом затухании можно с большой точностью считать, что максимальные отклонения от положения равновесия достигаются в моменты времени равные  , где  . В этом приближении найти путь  , который пройдет частица до полной остановки. Построить график зависимости .19.4.Чему равен логарифмический декремент затухания колебаний и добротность системы, если амплитуда затухающих колебаний уменьшилась в 10 раз за 50 колебаний? Построить график зависимости  .19.5. К пружине подвесили грузик, и она растянулась на 1 см. С каким периодом будет колебаться грузик в вертикальном направлении? Логарифмический декремент затухания равен 4. Построить график зависимости .19.6. Частицу сместили из положения равновесия на расстояние 1 см и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмический декремент затухания равен 0.020? Построить график зависимости .19.7. Энергия затухающих колебаний маятника, происходящих в некоторой среде, за время 2 мин уменьшилась в 100 раз. Определите коэффициент сопротивления, если масса маятника 100 г. Построить график зависимости .19.8. На колеблющийся шарик массы m на пружинке жесткостью k действует сила трения  . Подсчитайте тепло, выделяющееся в среднем за один период колебаний, предполагая, что добротность колебаний велика. На сколько уменьшится амплитуда колебаний за один период колебаний маятника? Построить график зависимости .19.9. Найти добротность математического маятника длины 0.5 м, если за 5.2 минуты его полная энергия уменьшилась в  раза? Построить график зависимости .19.10. Измерены три последовательных амплитуды смещения затухающих колебаний пружинного маятника 8.6, -4.1, 4.3 мм. Каково среднее положение осциллятора и логарифмический декремент затухания колебаний λ? Привести поясняющий рисунок и указать основные параметры 19.11. Колебательный контур имеет индуктивность 0.005 Гн, емкость конденсатора 0.2 мкФ. При каком логарифмическом декременте и омическом сопротивлении цепи энергия уменьшится на порядок за три полных колебания? Учесть, что в начальный момент времени заряд на конденсаторе был равен 1 нКл. Построить векторную диаграмму напряжений и привести графики  и зависимость энергии в  и  от времени.19.12. Колебательный контур имеет индуктивность 0.1 Гн, емкость конденсатора 0.9 мкФ. Сколько времени проходит от момента, когда конденсатор полностью разряжен, до момента, когда его энергия вдвое превышает энергию катушки? Активное сопротивление контура рано нулю. Построить графическое решение задачи. 19.13. Колебательный контур имеет индуктивность 25 мГн, емкость конденсатора 10 мкФ. Определите сопротивление контура, если амплитуда тока уменьшилась в е раз за 16 колебаний? Учесть, что в начальный момент времени заряд на конденсаторе был равен 1 нКл. Построить векторную диаграмму напряжений и привести графики 19.14. Колебательный контур с собственной частотой  кГц имеет добротность Q = 100. Рассчитайте емкость и индуктивность контура, если сопротивление, включенное в контур R = 5 Ом. Учесть, что в начальный момент времени заряд на конденсаторе был равен 1 нКл. Построить векторную диаграмму напряжений и привести графики .20. Вынужденные колебания. Резонанс. Переменный ток 20.1. Найдите усредненные значения кинетической и потенциальной энергии гармонического осциллятора под действием внешней гармонической силы в режиме установившихся колебаний. Как они соотносятся между собой при различных значениях частоты вынуждающих колебаний? Привести поясняющий рисунок и указать основные параметры 20.2. При какой скорости поезда рессоры его вагонов будут особенно сильно колебаться под действием толчков колес о стыки рельс, если длина рельс 12.5 м, нагрузка на рессору 5.5 тонн и если рессора прогибается на 16 мм при нагрузке в 1 тонну? Построить амплитудно-частотную характеристику. 20.3. Человек массой 60 кг качается на качелях. Его движения описывается уравнением  м. На качели начала действовать сила, изменяющаяся по закону  Н. Построить график зависимости .20.4. Амплитуды смещений вынужденных гармонических колебаний при частотах 500 Гц и 600 Гц равны между собой. Найдите частоту, при которой амплитуда смещений максимальна. Привести поясняющий рисунок и указать основные параметры 20.5. Амплитуды скорости вынужденных гармонических колебаний при частотах вынуждающей силы 500 Гц и 600 Гц равны между собой. Принимая, что амплитуда вынуждающей силы в обоих случаях одна и та же, найдите частоту, соответствующую резонансу скорости. Привести поясняющий рисунок и указать основные параметры. 20.6. Оценить, через сколько времени установятся колебания в системе с добротностью  и собственной частотой  рад/с при резонансном воздействии на эту систему вынуждающей гармонической силы. Привести поясняющий рисунок и указать основные параметры.20.7. Найти добротность осциллятора, у которого отношение резонансной частоты к частоте затухающих колебаний равно 0.97. Привести поясняющий рисунок и указать основные параметры. 20.8. При изменении частоты  вынуждающей силы, действующей на маятник, меняется фаза  установившихся колебаний и запасенная энергия  . Пусть при малом сдвиге частоты  Гц от резонансной частоты фаза колебаний изменилась на  . Как изменится при этом энергия ? Каково время релаксации  в режиме свободных колебаний? Привести поясняющий рисунок и указать основные параметры20.9. Под действием момента сил  тело совершает вынужденные крутильные колебания по закону  . Найти работу сил трения, действующих на тело, за период колебания. Принять:  Н·м,  рад,  рад/с,  . Привести поясняющий рисунок и указать основные параметры20.10. Шарик массы 50 г подвешен на пружинке жесткостью 20 Н/м. Под действием вынуждающей вертикальной гармонической силы с частотой 25 рад/с шарик совершает установившиеся колебания. При этом смещение шарика отстает по фазе от вынуждающей силы на  . Найти добротность осциллятора. Привести поясняющий рисунок и указать основные параметры20.11. К источнику переменного напряжения последовательно подключили катушку индуктивности 0.16 Гн, конденсатор емкостью 64 мкФ и сопротивление 2 Ом. Определить силу тока в цепи, если напряжение равно 220 В, а частота 200 Гц. При какой частоте наступит резонанс напряжений и каковы будут при этом сила тока и напряжение на зажимах катушки и конденсатора? Построить векторную диаграмму напряжений. 20.12. Для определения индуктивности дросселя его сначала включают в цепь постоянного тока, а затем в цепь переменного тока частотой 50 Гц. Параллельно к дросселю подключен вольтметр. Определить индуктивность дросселя, если при прохождения через него постоянного тока  А показания вольтметра  В, а при переменном токе  А соответствующее напряжение  В. Привести поясняющий рисунок и указать основные параметры и построить векторную диаграмму напряжений.20.13. Катушка с индуктивностью 50 мГн и активным сопротивлением 10 Ом подключена к источнику синусоидального напряжения, эффективное (действующее) значение которого равно 120 В, а частота 50 Гц. Определить полное сопротивление катушки и сдвиг фазы между током и напряжением. Построить векторную диаграмму напряжений. 20.14. В цепи переменного тока частотой 50 Гц находится резистор, катушка с индуктивностью 3 Гн и конденсатор с емкостью 4.7 мкФ. Между напряжением и силой тока наблюдается сдвиг фазы  . Чему равно сопротивление резистора и какую емкость надо включить последовательно в цепь, чтобы устранить сдвиг фазы? Построить резонансные кривые (АЧХ и ФЧХ).20.15. К источнику переменного напряжения частотой 50 Гц и напряжениием 220 В последовательно подключили катушку индуктивности 0.25 Гн, конденсатор емкостью 0.47 мкФ и резистор сопротивлением 2 Ом. Определить  . Построить резонансные кривые (АЧХ и ФЧХ).20.16. К источнику переменного напряжения частотой 50 Гц и напряжениием 220 В последовательно подключили катушку индуктивности 0.5 Гн, конденсатор емкостью 0.47 мкФ и резистор сопротивлением 10 Ом. Определить . Построить резонансные кривые (АЧХ и ФЧХ).20.17. Колебательный контур содержит катушку индуктивностью 6 мкГн и конденсатор емкостью 1.2 нФ. Для поддержания в колебательном контуре незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе 2 В необходимо подводить среднюю мощность 0.2 мВт. Считая затухание малым, определите добротность контура. Построить резонансные кривые (АЧХ и ФЧХ). 20.18. Колебательный контур содержит катушку индуктивностью 5 мкГн и конденсатор емкостью 0.47 мкФ. Для поддержания в колебательном контуре незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе 10 В необходимо подводить среднюю мощность 5 мВт. Считая затухание малым, определите добротность контура. Построить резонансные кривые (АЧХ и ФЧХ). 20.19. В цепь переменного тока с частотой 50 Гц последовательно включены резистор сопротивлением 100 Ом и конденсатор емкостью 22 мкФ. Определите, какая доля напряжения, приложенного к цепи, приходится на падение конденсатора и на резисторе. Построить векторную диаграмму напряжений. 20.20. К колебательному контуру, содержащему последовательно соединенные конденсатор и катушку с активным сопротивлением, подключено внешнее переменное напряжение, частоту которого можно менять, не меняя его амплитуды. При частотах 80 и 120 Гц амплитуды силы тока в цепи оказались одинаковыми. Определите резонансную частоту тока. Построить резонансные кривые (АЧХ и ФЧХ). ПРИЛОЖЕНИЕ А1.Теплопроводность воздуха при атмосферном давлении Таблица А.1
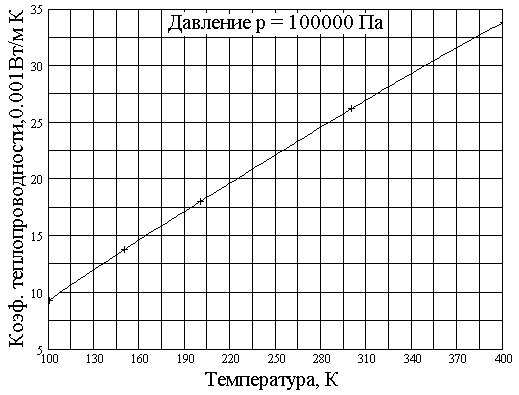 Рис.А.1. Зависимость коэффициента теплопроводности воздуха от температуры А2. Интерполяционные формулы Лагранжа 1.Линейная интерполяция на интервале [x1, x2] (заданы 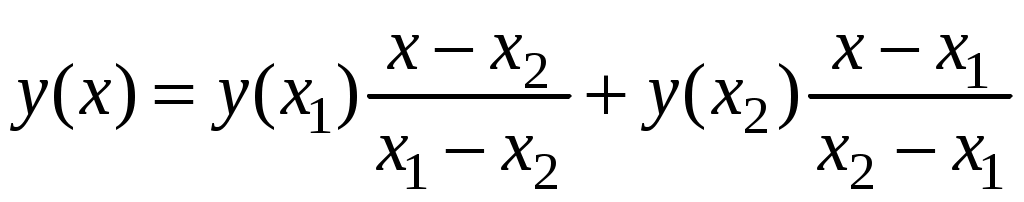 и  ) (А.1)2.Квадратичная интерполяция на интервале [x1, x3] (заданы 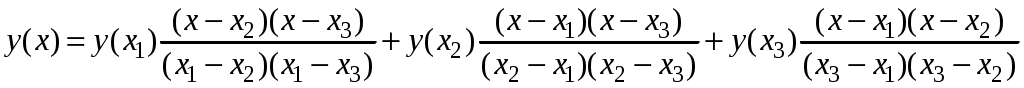 и  ) (А.2)A3. Решение системы линейных алгебраических уравнений. Метод Гаусса (BASIC) CLS DIM a(10, 10), b(10) INPUT "n="; n FOR i = 1 TO n FOR j = 1 TO n PRINT "a("; i; ","; j; ")="; INPUT a(i, j) NEXT j PRINT "b("; i; ")="; INPUT b(i) NEXT i PRINT "matrix" FOR i = 1 TO n FOR j = 1 TO n PRINT a(i, j); " "; NEXT j PRINT b(i) NEXT i FOR i = 1 TO n - 1 FOR j = i + 1 TO n a(j, i) = -a(j, i) / a(i, i) FOR k = i + 1 TO n a(j, k) = a(j, k) + a(j, i) * a(i, k) NEXT k b(j) = b(j) + a(j, i) * b(i) NEXT j NEXT i x(n) = b(n) / a(n, n) FOR i = n - 1 TO 1 STEP -1 h = b(i) FOR j = i + 1 TO n h = h - x(j) * a(i, j) NEXT j x(i) = h / a(i, i) NEXT i FOR i = 1 TO n PRINT "x("; i; ")="; x(i) NEXT i END Литература 1. Савельев И.В. Курс общей физики. - М.: Наука, Т 1,2. 2. Сивухин Д.В. Курс общей физики. - М.: Наука, Т 1,2,3. 3. Практикум по решению физических задач с применением компьютера. Молекулярная физика и термодинамика / Штыгашев А.А. Новосибирск: НГТУ, 2016. -64 с. 4. Штыгашев А.А. Решение задач на компьютере. Электричество и магнетизм. Новосибирск: НГТУ, 2017. -145 с. 5. Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MatLab 7 СПб.: БХВ-Петербург, 2005. 1104 с. 6. Штыгашев АА Применение ПЭВМ в решении задач по физике (механика) Новосибирск: НГПУ, 1999. -112 с. 7. Штыгашев А. А., Пейсахович Ю.Г. Задачи по физике. Механика. Молекулярная физика и термодинамика. Электричество : учеб. пособие - Новосибирск : Изд-во НГТУ, 2017. - 160 с. 8. Физические величины: Справочник / Под ред. И.С.Григорьева, Е.З.Мейлихова. – М.: Энергоатомиздат, 1991. – 1232 с 1 Программу писать не обязательно, но приветствуется, за что ставятся дополнительные баллы. |
,
Вт/(м К)