заебца. ргз электроника. Расчетнографическое задание 1 по дисциплине Электроника
 Скачать 102.42 Kb. Скачать 102.42 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА АВТОМАТИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И ПРОИЗВОДСТВ РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №1 по дисциплине «Электроника» Вариант №76 Выполнил : Зыков Е.А. Группа 7419 Дата сдачи:_________________________ Подпись:_________________ Проверил: Черемисина С.А., доцент. Подпись:___________________________ Благовещенск, 2021 Содержание: Задача 1……………………………………………………………….……3 Задача 2……………………………………………………………….……4 Задача 3……………………………………………………………….……5 Задача 4……………………………………………………………….……6 Задача 5……………………………………………………………….……6 Задача 6……………………………………………………………….……8 Задача 7……………………………………………………………….……9 Задача 8……………………………………………………………….…....9 Задача 9……………………………………………………………….…..11 Задача 10..…………………………………………………………….….11 Вариант 76
Задача 1. Переводим значение температуры в градусы Кельвина 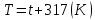 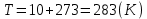 Ширина запрещённой зоны при заданной температуре для Si 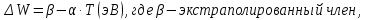 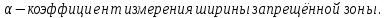 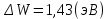 Эффективная масса электрона 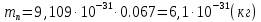 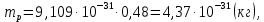 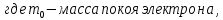 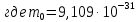 Среднее геометрическое значение эффективных плотностей энергетических состояний в зоне проводимости и валентной зоне N: 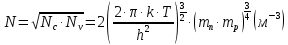 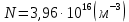 Равновесные концентрации электронов и дырок 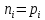 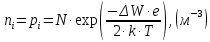 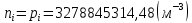 Задача 2. Концентрация основных носителей (электронов) в электронном полупроводнике 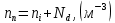 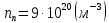 Концентрация неосновных носителей (дырок) в электронном полупроводнике 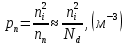 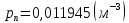 Концентрация основных носителей (дырок) в дырочном полупроводнике 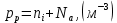 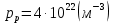 Концентрация неосновных носителей (электронов) в дырочном полупроводнике 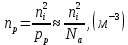 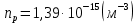 Задача 3. Уровень Ферми в собственном полупроводнике находится приблизительно в середине запрещенной зоны и, при условии 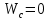 , определяется выражением , определяется выражением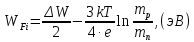 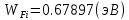 Уровень Ферми в примесном полупроводнике p-типа определяется выражением 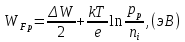 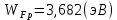 Уровень Ферми в примесном полупроводнике n-типа определяется выражением: 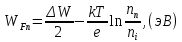 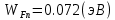 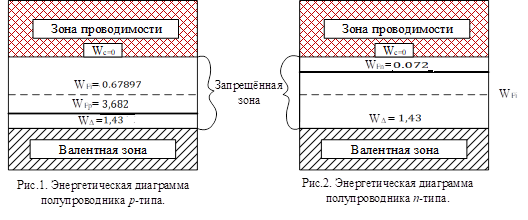 Рисунок 1 – Энергетическая диаграмма полупроводника Задача 4. Высоту потенциального барьера (контактную разность потенциалов) в идеальном электронно-дырочном переходе в состоянии равновесия, т.е. при отсутствии внешнего напряжения можно определить: 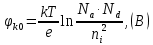 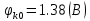 Задача 5. Ширина идеального электронно-дырочного перехода в состоянии равновесия δ0 определяется выражением 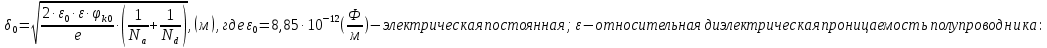   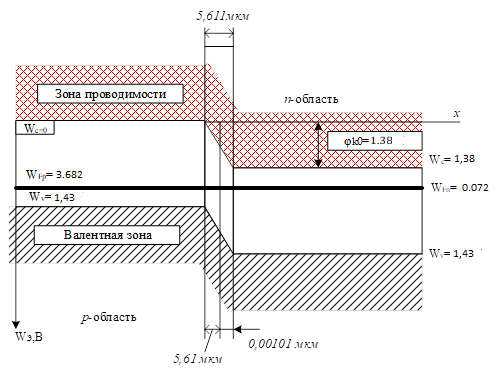 Рисунок 2 - Энергетическая полупроводниковая p-n-перехода в состоянии равновесия Размеры обедненных слоев p- и n- областей (δp0, δn0) в состоянии равновесия зависят от концентрации донорных и акцепторных примесей: 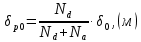 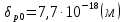 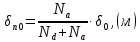 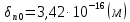 Проверка 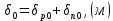 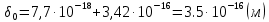 Задача 6. Определение параметров переходов при подаче внешнего напряжения. При подаче внешнего обратного напряжения высота потенциального барьера в идеальном p-n-переходе увеличивается 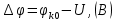 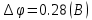 Уровень Ферми в пределах p-nперехода смещается на величину поданного фиксированного внешнего напряжения U. При подаче внешнего обратного напряжения ширина электронно-дырочного перехода увеличивается:  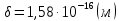 Размеры обедненных слоев p- иn- областей: 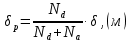 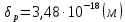 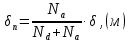 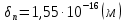 Проверка: 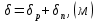 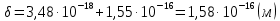 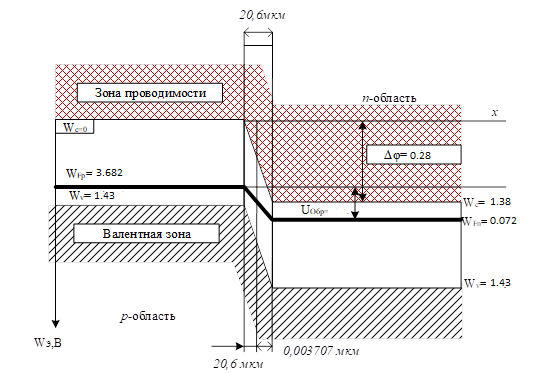 Рисунок 3 - Энергетическая диаграмма р-n – перехода при подачи внешнего обратного напряжения Задача 7. Определение паразитных емкостей перехода. Суммарная ёмкость p-n-перехода С складывается из барьерной емкости Сб и диффузионной емкости Сд. Диффузионная ёмкость оказывает влияние при прямом включении. Так как, в заданном варианте- включение обратное, то рассчитываем только барьерную емкость перехода 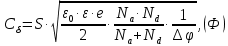 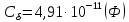 Задача 8. Определение удельных сопротивлений и проводимостей p- и n- областей, образующих электрический переход. Подвижности носителей заряда μn и μp зависят от температуры T и концентрации примесей 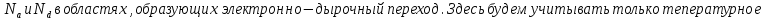 изменение подвижности заряда. Для Германия (Ge) 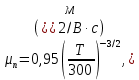 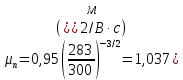 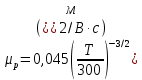 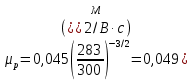 С учетом того, что концентрации основных носителей много больше концентрации неосновных, проводимости полупроводников можно рассчитать по приближенным формулам: для электронного полупроводника 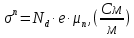 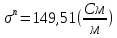 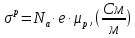 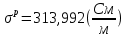 Удельные объёмные сопротивления p- и n- областей 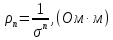 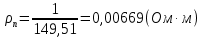 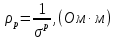 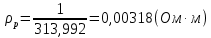 Задача 9. Определение обратного тока в переходе. Коэффициенты диффузии зависят от температуры и подвижности носителей заряда: 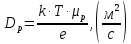 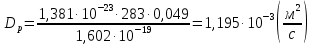 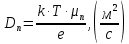 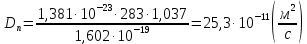 Обратный ток (ток насыщения или ток экстракции идеального p-nперехода): 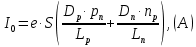 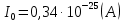 Задача 10. Определение силы тока и статического сопротивления при заданном внешнем напряжении. Сила тока в переходе I и приложенное к переходу внешнее напряжение U связаны уравнением ВАХ электрического перехода: 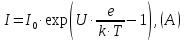 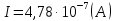 Статическое сопротивление p-n- перехода 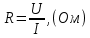 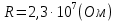 |

 20
20 22
22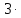 10-7
10-7