Штыгашев РГЗ Физика. РГЗ1. Расчетнографическое задание 1
 Скачать 284.58 Kb. Скачать 284.58 Kb.
|
|
Министерство образования и науки РФ Федеральное агентство по образованию НГТУ Кафедра общей физики Расчетно-графическое задание №1 Вариант 25
Факультет: Преподаватель: Штыгашев А.А. Группа Студент: Новосибирск 2023 Задача №1. Постановка задачи: Камень бросили с крутого берега вверх под углом 30 градусов к горизонту со скоростью 12 м/с. Какая дальность полета камня и с какой высоты был брошен камень, если время полета 3 с. Сопротивлением воздуха пренебречь. Построить график скорости от времени и график траектории движения камня. Дано: 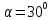 м м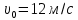 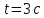 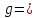 9,8 9,8  Найти   Рисунок 1. Движение камня Решение: Математическая модель: Вдоль оси х тело движется равномерно со скоростью  . Вдоль оси оу (по вертикали) имеем движение тела, брошенного вертикально вверх с начальной скоростью . Вдоль оси оу (по вертикали) имеем движение тела, брошенного вертикально вверх с начальной скоростью  . . Для проекций скорости в любой момент времени, движения можно записать следующие уравнения 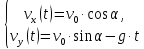 Модуль вектора скорости определится как: 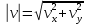 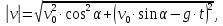 Зависимость от времени координаты тела у: 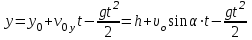 В момент падения на Землю 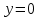 : :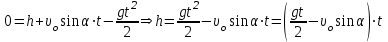 Дальность полета тела: 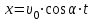 Подставим числа:  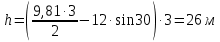  График скорости от времени движения камня.  Рисунок 2. Скорость движения от времени Ответ:  Задача №2. Постановка задачи: Тело пустили снизу вверх по наклонной плоскости, составляющей угол  с горизонтом. Найти коэффициент трения скольжения, если время подъема оказалось в с горизонтом. Найти коэффициент трения скольжения, если время подъема оказалось в 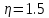 раза меньше времени спуска. раза меньше времени спуска.Дано: m1=m2  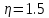 Найти:  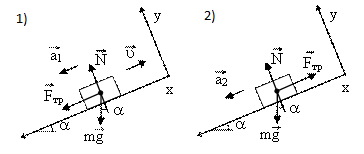 Рисунок 3. Схема движения тела Решение: При движении тела вверх по наклонной плоскости (рис. 3.1) на него действуют три силы: сила тяжести  , сила нормальной реакции N и сила трения , сила нормальной реакции N и сила трения  . Основной закон динамики запишется в виде: . Основной закон динамики запишется в виде: 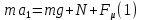 В проекциях на оси координат это уравнение имеет вид:  Из второго уравнения следует 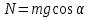  . Подставив выражение для . Подставив выражение для  в первое уравнение, получим: в первое уравнение, получим: 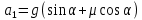 При движении тела вниз по наклонной плоскости (рис. 3.2) на него действуют те же силы, но сила трения направлена в сторону, противоположенную движению. Второй закон Ньютона для тела запишется в виде:  в проекции на оси координат:  В этом случае  . Длина пути S при подъеме и спуске тела одинаковая: . Длина пути S при подъеме и спуске тела одинаковая: Из формулы (3) следует: 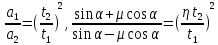  Окончательно: 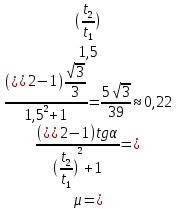 Ответ:  Задача №3. Постановка задачи: Два свинцовых шара массами 2 кг и 3 кг подвешены на нитях длиной 1 м так, что касаются друг друга. Меньший шар отклонили на угол 45 градусов и отпустили. Считая удар центральным и неупругим, определите высоту, на которую поднимутся шары после удара. Найдите энергию, израсходованную на деформацию шаров. Постройте график зависимости высоты подъема шаров от начального угла. Дано:  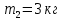  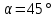 Найти: 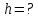   Рисунок 4. Постановочный рисунок к задаче №3. Решение: По закону сохранения энергии:  откуда: 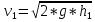   По закону сохранения импульса:  откуда:  Применим закон сохранения энергии для системы в момент когда оба шара поднимутся на максимальную высоту h: 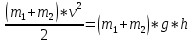 отсюда: 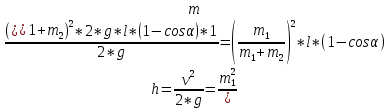 Подставляя исходные данные, получаем:  Энергия, израсходованная на деформацию шаров равна разности максимальной кинетической энергии малого шара и максимальной кинетической энергии обоих шаров после удара:  Подставив исходные данные, получаем: 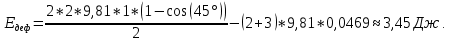 Псевдокод: begin; m1=2; // Масса малого шара, кг m2=3; // Масса большого шара, кг l=1; // Длина нити подвеса, м alpha=45; // Угол отклонения малого шара, град g=9.81; // Ускорение свободного падения, м/с^2 alphar=alpha*pi/180; // Перевод угла отклонения в радианы h=((m1/(m1+m2)).^2)*l*(1-cos(alphar))*100; // вычисляем высоту, на которую поднимутся шары после удара [см] Edef=m1*g*l*(1-cos(alphar))-(m1+m2)*g*h/100; // вычисляем энергию, израсходованную на деформацию шаров [Дж] end; Построим график зависимости высоты подъема шаров от начального угла:  Рисунок 5. Зависимость высоты подъема шаров от начального угла Ответ: 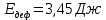  Задача №4. Постановка задачи: К ободу однородного валика радиусом 0,25 м приложена постоянная касательная сила 100 Н. При вращении на диск действует сила трения, момент которой равен 8,0 Нм. Определить массу диска, если известно, что он вращается с постоянным угловым ускорением  . Построить график кинетической энергии от времени в первые 10 с. . Построить график кинетической энергии от времени в первые 10 с.Дано: r = 0.25 м F=100 Н  =8 Нм =8 Нм рад/с2 рад/с2t=10 с Найти:   Рисунок 6. Постановочный рисунок к задаче №4 Решение: Модуль результирующего момента сил, действующего на диск:  где: 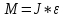 - момент сил вращательного движения диска. Момент инерции диска выражается по формуле: 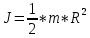 Отсюда масса диска: 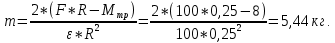 Кинетическая энергия вращающегося тела выражается по формуле:  Псевдокод: begin; R=0.25; // Радиус валика, м F=100; // Касательная сила, приложенная к валику, Н Mf=8; // Момент трения, действующий на диск, Н*м eps=100; // Угловое ускорение вращающегося диска, рад/с^2 m=2*(F*R-Mf)/(eps*R.^2); // Определяем массу вращающегося диска, кг t=0:1:10; Ek=(m*R.^2)/4*(eps*t).^2; end; 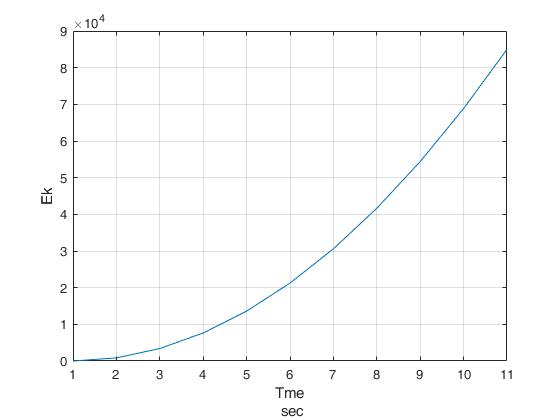 Рисунок 7. График зависимости кинетической энергии от времени Ответ: 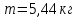 Задача №5. Постановка задачи: После запуска модели ракеты, модель выбрасывает ежесекундно газ массой 90 г со скоростью  м/с относительно корпуса. Начальная масса ракеты м/с относительно корпуса. Начальная масса ракеты  г. Какова наибольшая скорость ракеты, если масса ее топлива равна 200 г. Сопротивлением воздуха пренебречь. Построить графики временных зависимостей скорости и массы ракеты. г. Какова наибольшая скорость ракеты, если масса ее топлива равна 200 г. Сопротивлением воздуха пренебречь. Построить графики временных зависимостей скорости и массы ракеты.Дано:   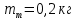 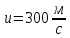 Найти:  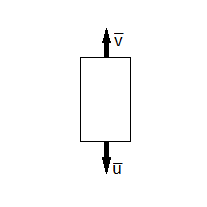 Рисунок 8. Постановочный рисунок к задаче №5 Решение: Определим конечную скорость ракеты по формуле Циолковского: 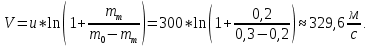 Массу и скорость ракеты определим по следующим временным зависимостям: 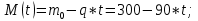  Псевдокод: begin; mv=90; // скорость выброса газа, г/с; u=300; // скорость выброса газа, м/с; m0=300; // начальная масса ракеты, г mf=200; // масса топлива, г V=u*log(1+mf/(m0-mf)); // Построим графики временных зависимостей скорости и массы ракеты t=0:0.1:(mf/mv); M=m0-mv*t; di=size(M); M0=ones(1,di(2))*m0; Vt=u*log(M0./M); plot(t,[M' Vt']); end; 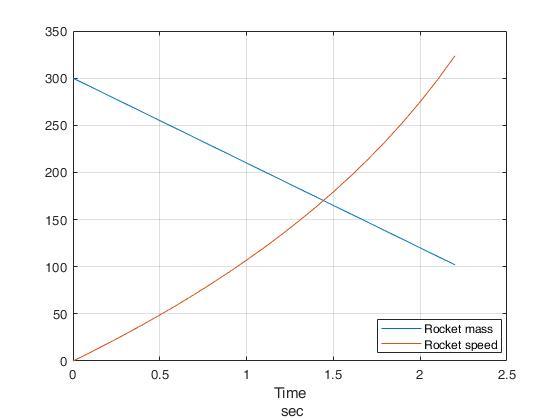 Рисунок 9. Зависимости скорости и массы ракеты от времени. Ответ:  |
