Шпаргалка по линейной алгебре. Рассказать о векторах на плоскости и в пространстве. Дать определение модуля вектора, нулевого вектора, коллинеарных векторов. Определить сложение и вычитание векторов. Дать определение произведения вектора на число

• Название: Рассказать о векторах на плоскости и в пространстве. Дать определение модуля вектора, нулевого вектора, коллинеарных векторов. Определить сложение и вычитание векторов. Дать определение произведения вектора на число
• Анкор: Шпаргалка по линейной алгебре.doc
• Дата: 13.05.2018
• Размер: 0.81 Mb.
• Имя файла: Шпаргалка по линейной алгебре.doc
• Тип: Документы; #19187
• Категория: Математика
• страница: 3 из 5

14) Прямую можно как линию пересечения 2-х непараллельных плоскостей 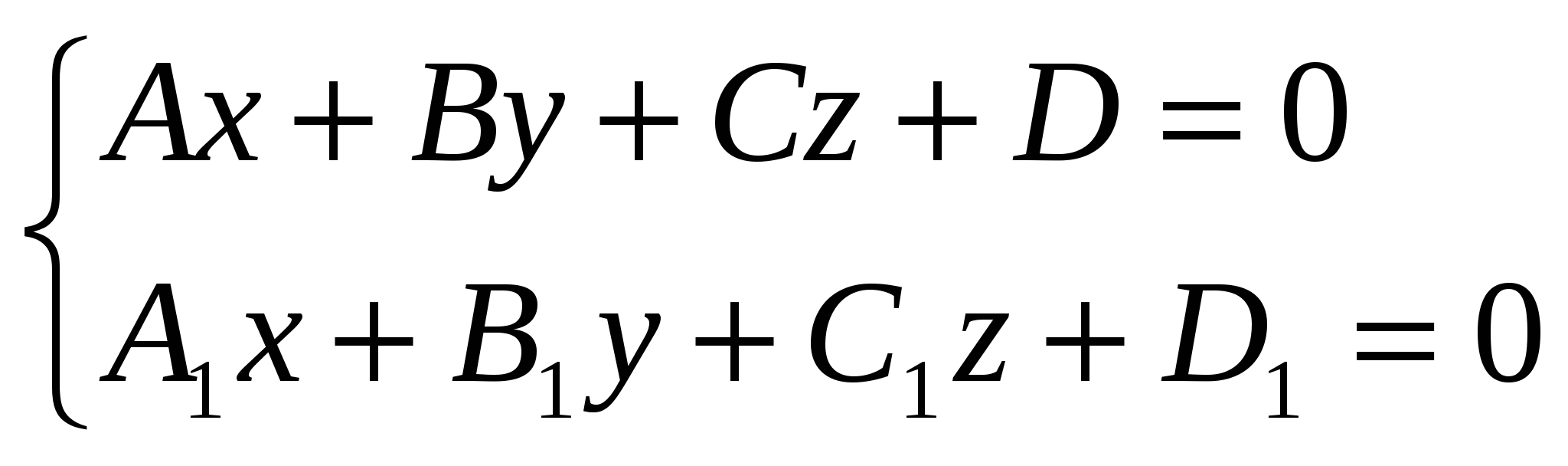система опред. пря-ую как геометр место точек пространства. Для канонического ур-ия: коорд. т. М получаем из системы придав к примеру х=0. Т.к прямая ито направляющий вектор принимаем за векторное произв. *

15)Пусть прямые заданы ур-ми и под углом понимают угол между направляющими =(;;) и =(;;) поэтому cos=.Если прямые то cos=0 т.е ++=0.Если прямые то т.е /=/=/

16)Наидем точку пересечения прямой 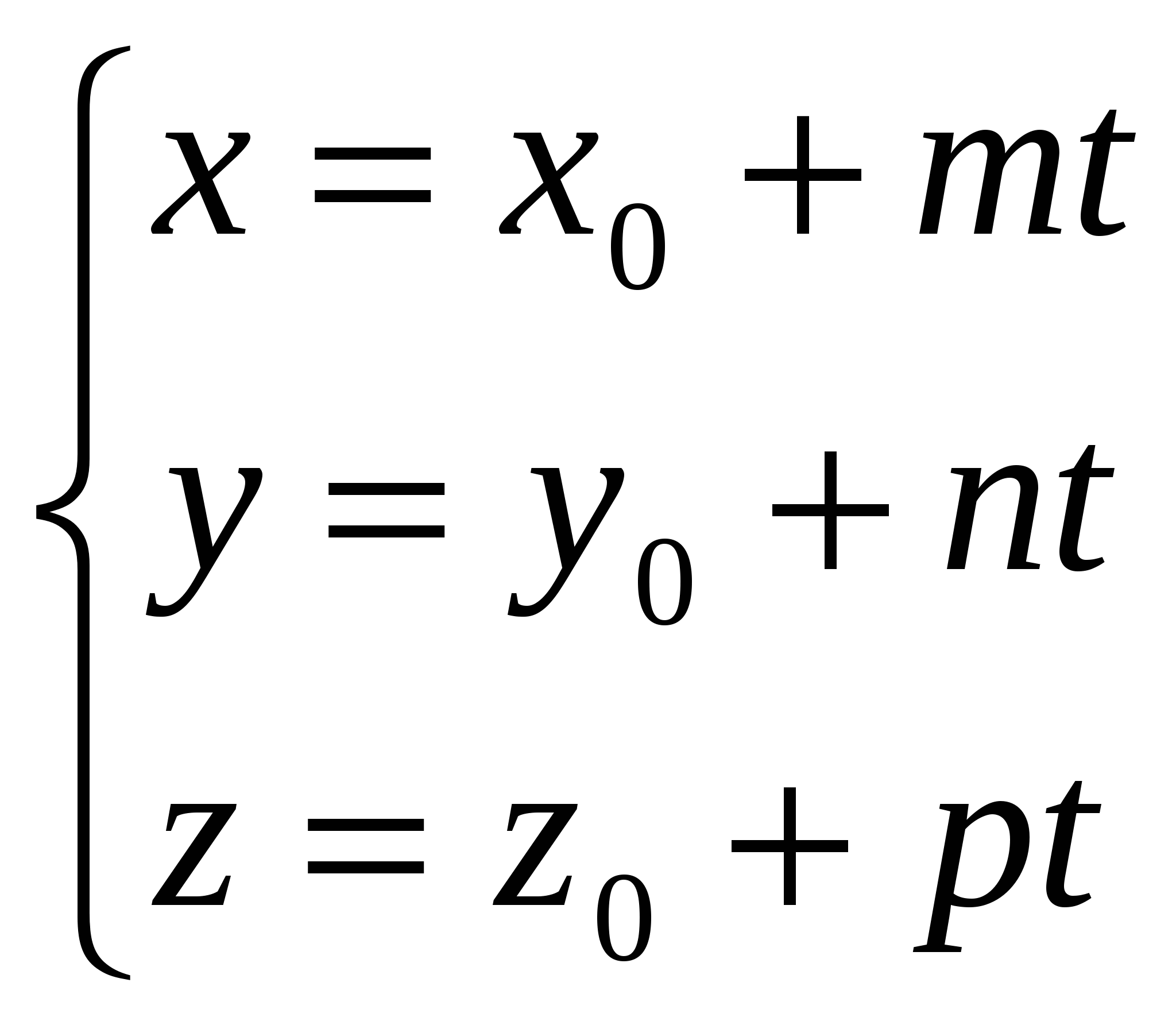с плоскостью Ax + By + Cz+D=0 для этого запишем ур-ие прямой в параметрическом виде подставляем эти выражения в ур-ия плоскости и получаем знач. t подставляем наиденое знач. параметрич. ур-ие и находим точку.

Угол назыв. любой из 2-х смежных углов. Образованный прямой и ее проекцией на плоскость sin=/

Если Lто т.е *=0 или Аm+Bn+Cp=0

Если Lто т.е А/m=B/n=C/p

17)Наидем ур-ие пл-сти проходящей через 3 точки ,,не лежащие на одной прямой. Возьмем произвольную точку М и составим векторы , ,Эти векторы компланарны. Используем условие компланарности 3-х векторов **=0

18) d=

19)Пусть L проходит через 2 точки (;)и(;).Ур-ие прямой проходящей через точку имеет вид: у-=k(x-).Т.к L проходит через т. то коорд. этой т. должны удов. ур-ию : -=k(-) отсюда k=-/-подставляем знач. k имеем у-/-= x-/- - ур-ие прямой L проходящей через 2 точки.

Вектор прямой есть направляющии вектор. (х-;у-) =

х-/m= у-/n каноническое ур-ие.

20)Пр: Ax + By + C = 0; В0 то х +у+=0у=kх+b где b= - k= - это ур-ие с угловым коэфф. угол наклона прямой к оси Ох. (;) и (;); =k+b и =k+b тогда -=k(-)k=-/-=tg. k есть tgпрямой к оси Ох

у=kх+bх=0 то у=b b-величина отрезка отсекаемого от оси Оу считая от начала координат.

Если прямые заданы ур-ми с угловым коэффициентом, то усл.состоит в равенстве их угловых коэффициентов: k1 = k2.

Для случая, когда прямые заданы уравнениями в общем виде /=/

Если прямые заданы ур-ми с угловым коэффициентом, то усл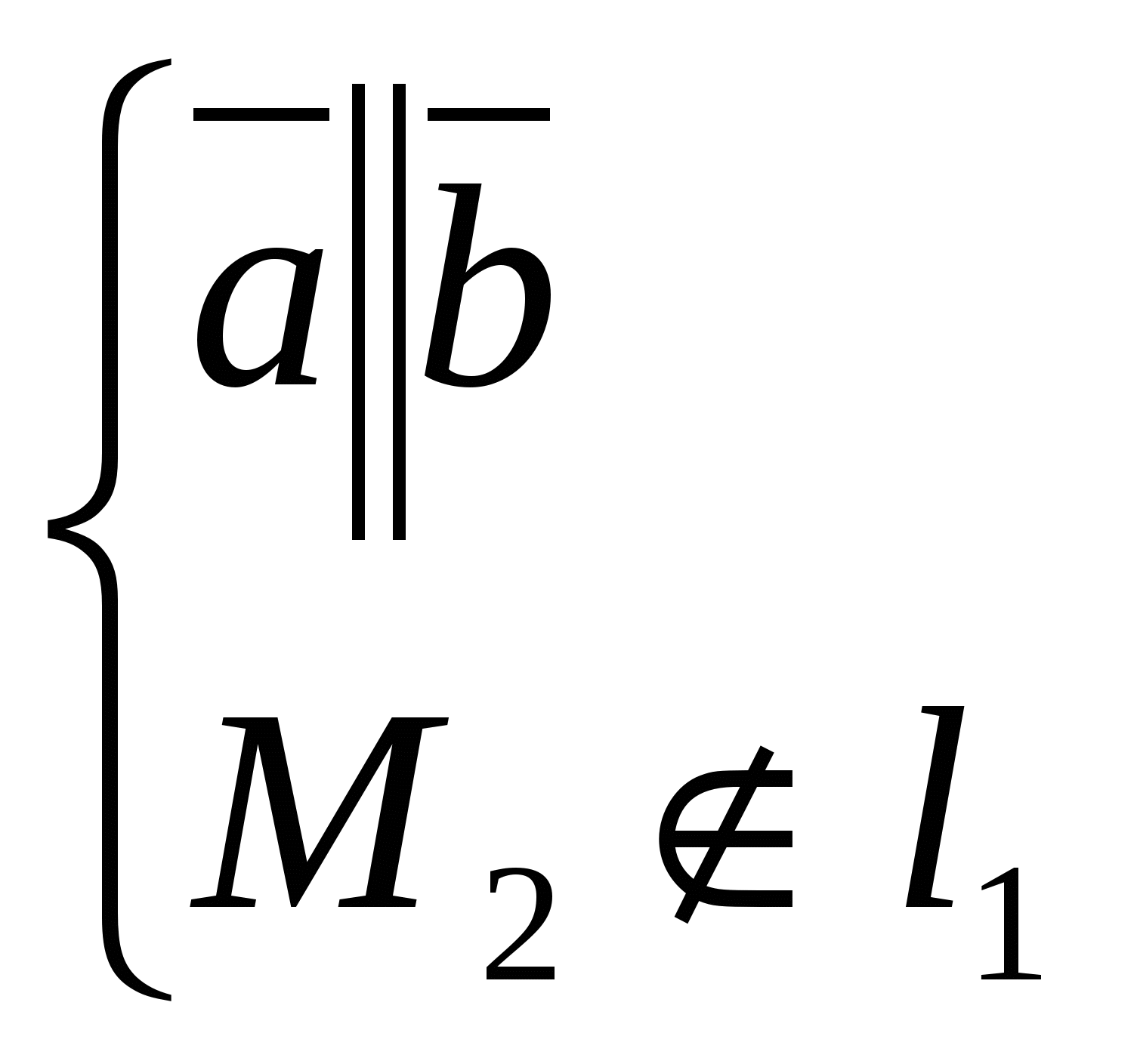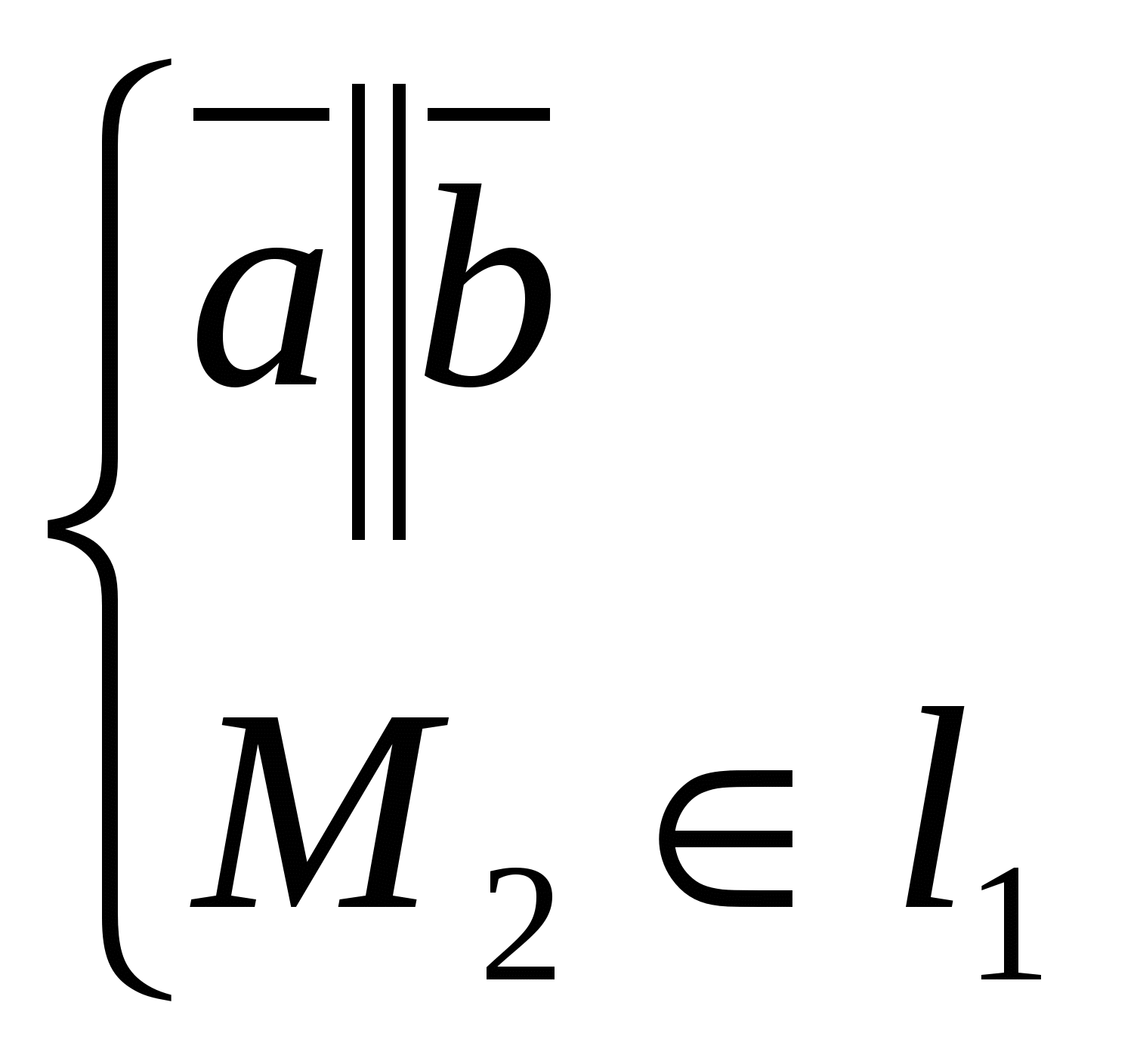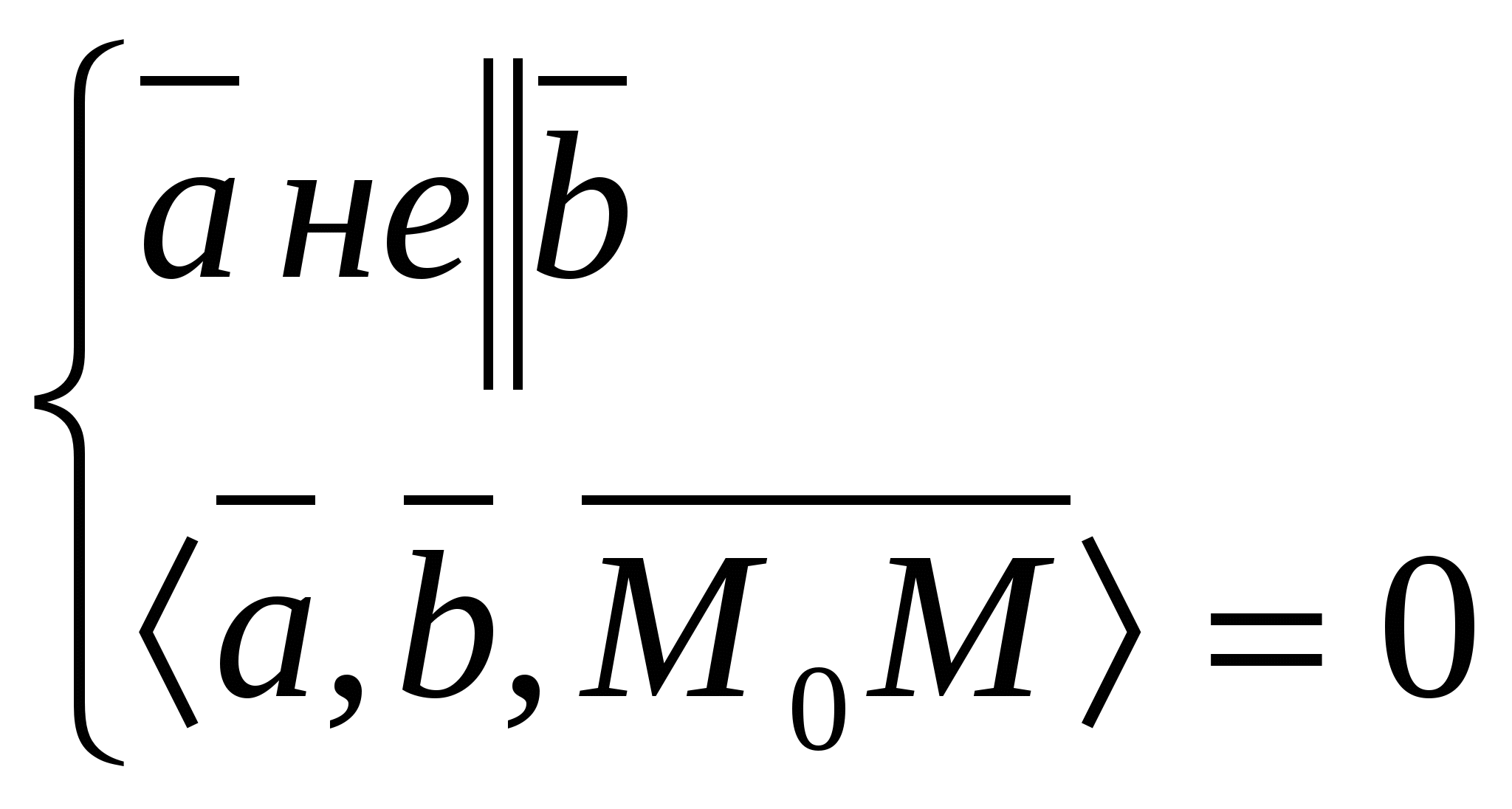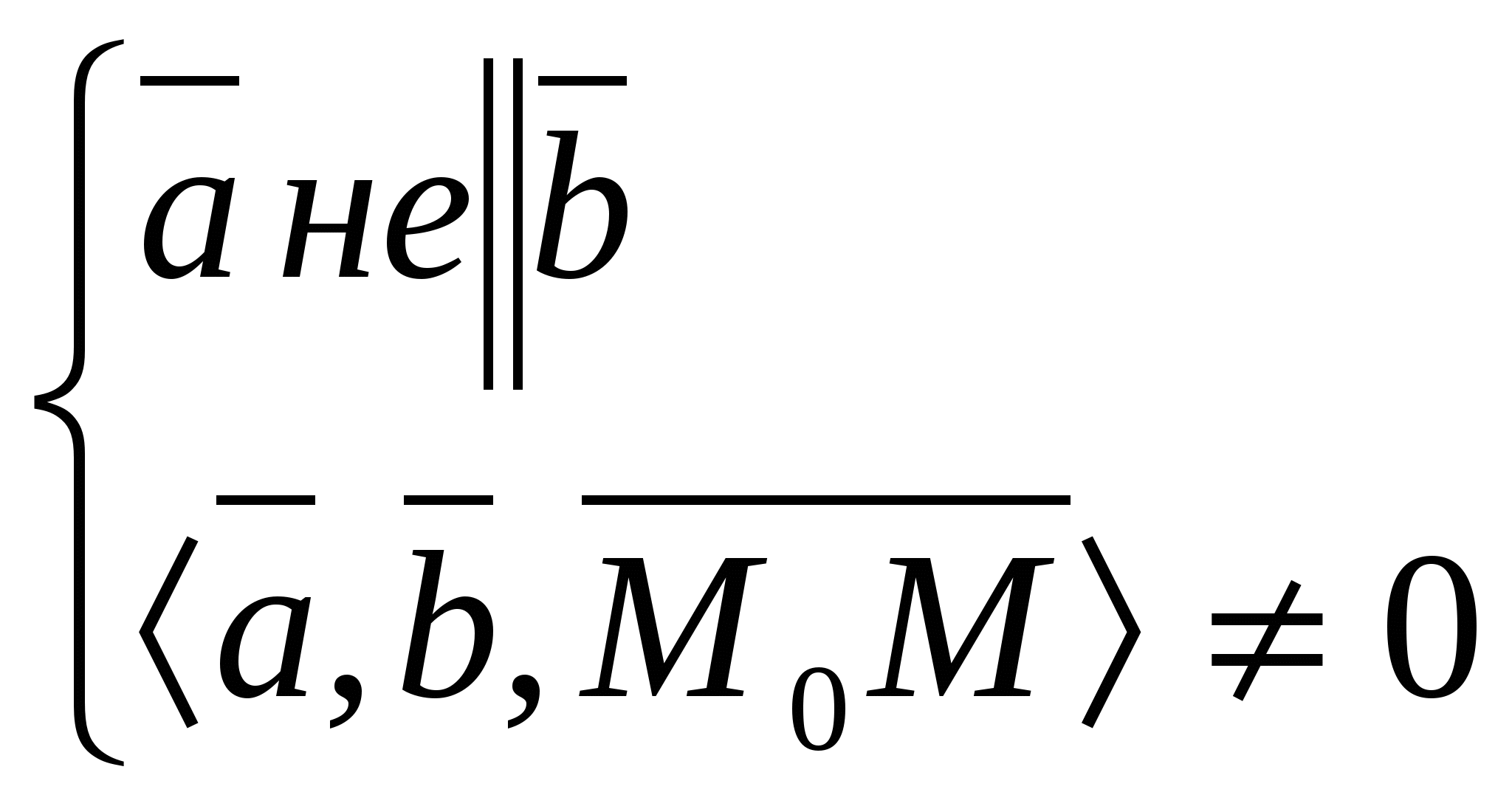.состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е. k= - 1/

21) = пересекает скрещивается

22)Матрицей назыв. прямоугольная таблица чисел содерж. m строк и n столбцов т.е размера mn b пишут . Ее вид … Произведение 2-х матриц возможно только если число столбцов 1-ой равно числу строк 2-ой.Элемент i-ой строки и j-ого столбца матрицы произведения равен сумме произведении эл-тов i-ой строки матрицы А на соответсвующие эл-ты j-ого столбца матрицы В.

*=; =

23)Система линеиных алгебраических ур-ии есть система вида 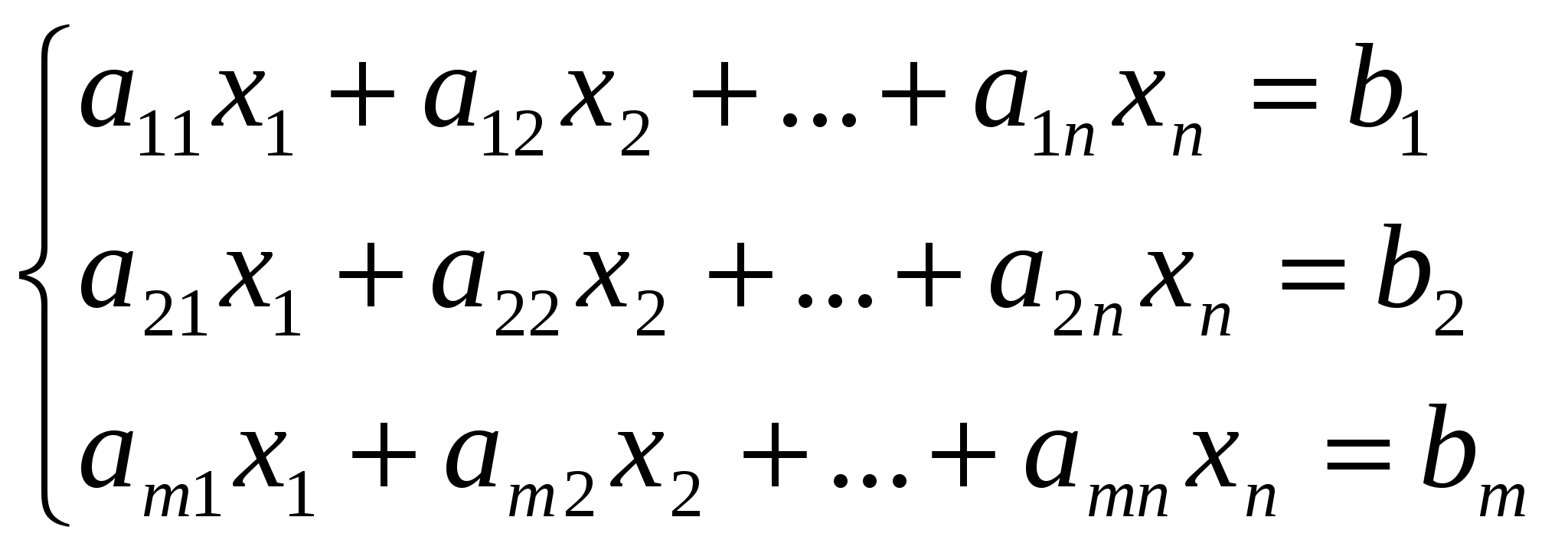Матричная форма А*Х=В.Основная матрица содержит только коэффициенты системы.Расширенная матрицадополнена столбцом свободных членов.

Эл-ные преобразованияне меняют мн-ва решении системы Ах=b.

1) перестановка местами 2-хрядов матрицы(опред меняет знак)

2)умножение строки на число(опред умножается на противоположное число)

3)прибавление к одной строки другой умноженной на число. (опред не меняется)

24)Матрица ступенчатая если главный элемент любой ее строки находится в столбце с большим номером чем гл. эл-т предыдущей строки а нулевые строки расположены под ними. Любая матрица преобразовывается в ступенчатую с помощью эквивалентных преобразовании: 1) Перемена местами строк (2)Умножение строки на число (3) прибавление к строке другой умноженной на число.Алгоритм:1)выбираем гл. ст-ку и меняем ее с первой(2)”Вырезаем”первую ступеньку.К строке с номером j у которой гл эл-т не ноль, прибавляем 1-ю строку умноженную на = -/(3)повторяем деиствие со следующей строкой.

25)Матрица у которой все гл. эл-ты всех строк равны 1 и над ними расположены нулиесть главная ступенчатая.Алгоритм:1)выбираем гл. ст-ку и меняем ее с первой(2)”Вырезаем”первую ступеньку.К строке с номером j у которой гл эл-т не ноль, прибавляем 1-ю строку умноженную на = -/(3)повторяем деиствие со следующей строкой.(4)Зануляем эл-т стоящие над гл. эл-ми прибавляя верхнюю строку к нижней уиноженой на = -/