Шпаргалка по линейной алгебре. Рассказать о векторах на плоскости и в пространстве. Дать определение модуля вектора, нулевого вектора, коллинеарных векторов. Определить сложение и вычитание векторов. Дать определение произведения вектора на число
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
26)Квадратной матрице А порядка n можно составить число del A число которое может быть вычислено по элементам матрицы по формуле: del A= 27)Определитель второго порядка вычисляется по формуле: Определитель третьего порядка вычисляется по формуле:из 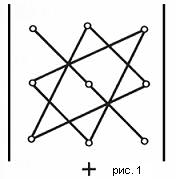 вычитаем вычитаем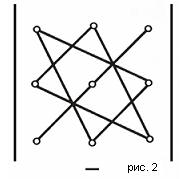 Если D = |A| - определитель порядка n, то минором Mij элемента 28)Если матрица содержит нулевую строку, то ее определитель равен нулю. 29)Определитель имеющий 2 одинаковых ряда равен нулю. Если к одной строке прибавить другую умноженную на число то определитель не изменится. 30)Определитель с 2-мя одинаковыми строками равен нулю. 31) Эл-ные преобразования: 1) перестановка местами 2-хрядов матрицы(опред меняет знак) 2)умножение строки на число(опред умножается на противоположное число) 3)прибавление к одной строки другой умноженной на число. (опред не меняется) 32)Минор некоторого эл-та Алгебраическим дополнением элемента Разложение определителя По элементам i-й строки: 33)Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая Итак, чтобы найти обратную матрицу нужно: 1)Найти определитель матрицы A. 2)Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу, элементами которой являются числа Aij. 3)Найти матрицу, транспонированную полученной матрице , и умножить её на 1/ 34)Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая Метод Гаусса. Н  а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. где а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. где На втором этапе последовательно находятся все неизвестные, начиная с предпоследней. 35)Система линеиных алгебраических ур-ии есть система вида 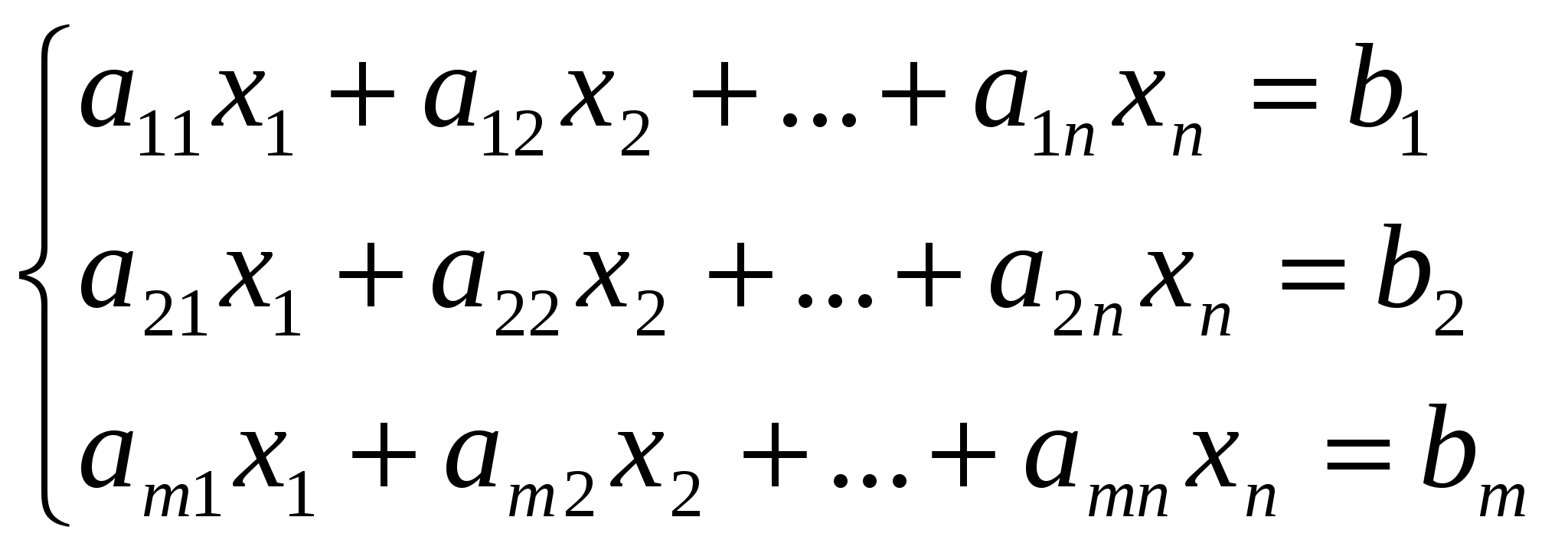 Формулы Крамера. В случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: Формулы Крамера. В случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:36)Система линеиных алгебраических ур-ии есть система вида 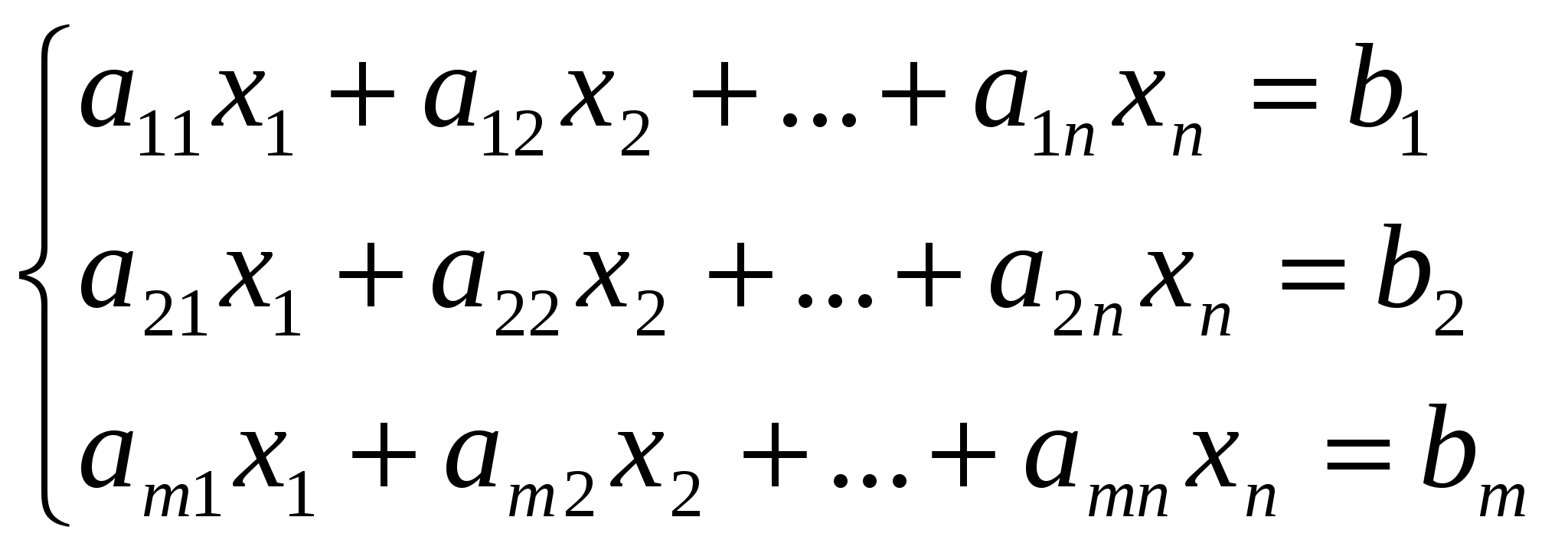 Метод Гаусса. Метод Гаусса.Н  а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. где а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. гдеНа втором этапе последовательно находятся все неизвестные, начиная с предпоследней. Система имеет бесконечное число решении если есть свободные неизвестные. 37)Квадратная матрица назыв. невыраженной если опред del A 38)Система линеиных алгебраических ур-ии есть система вида  Метод Гаусса. Метод Гаусса.Н  а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. где а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. гдеНа втором этапе последовательно находятся все неизвестные, начиная с предпоследней. Система имеет единственное решение если все неизвестные главные 39) Система линеиных алгебраических ур-ии есть система вида  Метод Гаусса. Метод Гаусса.Н  а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. где а первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных далее приводится к виду, когда диагональ, состоящая из единичек отсекает нули. гдеНа втором этапе последовательно находятся все неизвестные, начиная с предпоследней. Система не имеет решений если главный эл-т расположен в последнем столбце. 40)Наибольший из порядков миноров данной матрицы отличный от нуля есть ранг матрицы r(A) или rangA. Метод нахождения ранга: 1) Приводим матрицу к ступенчатой число ненулевых и есть ранг. Т.к ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы, то для однородной системы ранг расширенной матрицы равен рангу основной поэтому система всегда совместна. 41)Комплексное число z=x+iy можно изобразить т. М(х;у) пл-сти Оху где х=Rez y=Imz. На комплексной плоскости изображаются комплексные числа.Ось абсцисс – действительная ось,оси ординат – мнимая ось. Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости. Алгебраическая форма z=x+iy. Сумма 2-х компл. чисел z=x+iy и Вычитание z- Произведение z 42)Комплексное число z=x+iy можно задать с помощью радиус-вектора 43)Деление определяется как действие обратное умножению.Частное 2-х компл.  таким образом z= таким образом z=Для тригонометрической формы: 44) 45)Модуль и арг. компл. числа можно рассматривать как полярные координаты вектора 47)Формула Муавра, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид: |
