|
Шпаргалка по линейной алгебре. Рассказать о векторах на плоскости и в пространстве. Дать определение модуля вектора, нулевого вектора, коллинеарных векторов. Определить сложение и вычитание векторов. Дать определение произведения вектора на число
48)n-Мерным вектором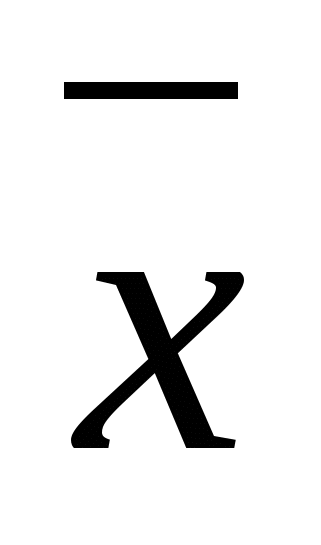 называется упорядоченный набор из n действительных чисел, записываемых в виде строки называется упорядоченный набор из n действительных чисел, записываемых в виде строки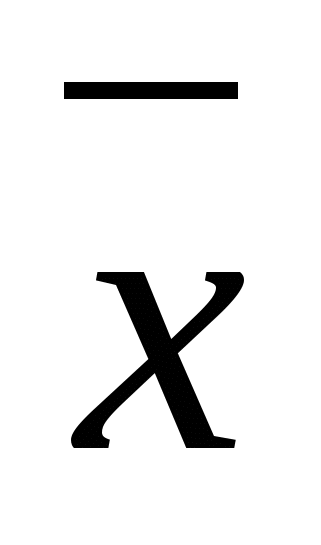 =( =(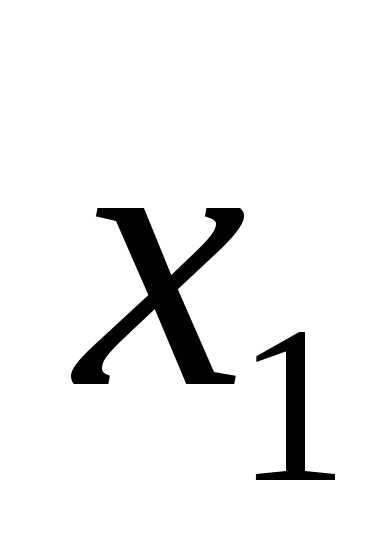 ; ;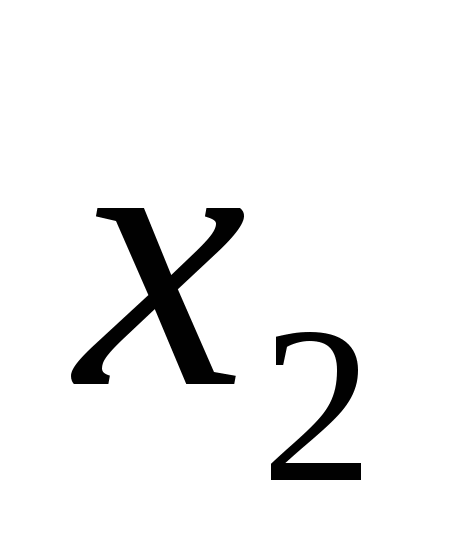 ;…; ;…;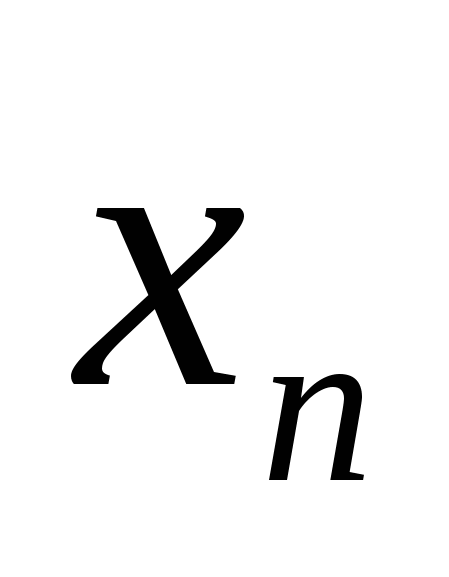 )Число )Число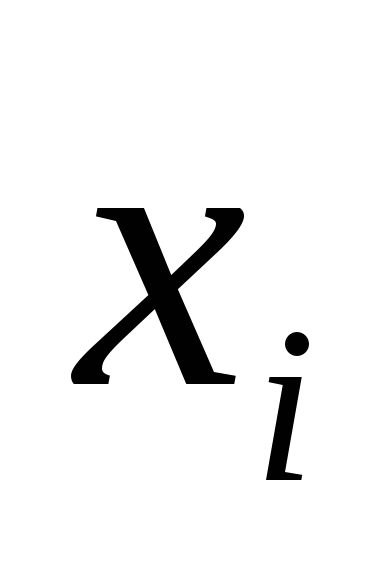 называют i-й координатой вектора называют i-й координатой вектора 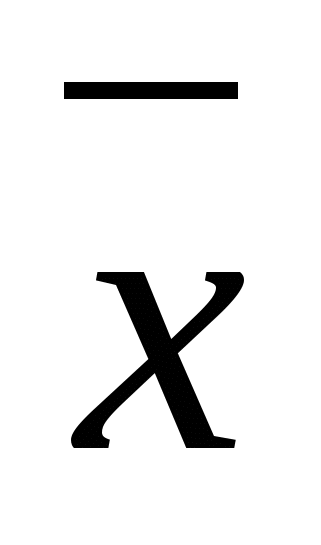 . Многомерное пространство,пространство, имеющее число измерений (размерность) более трёх. . Многомерное пространство,пространство, имеющее число измерений (размерность) более трёх.
Произведением вектора на действительное число 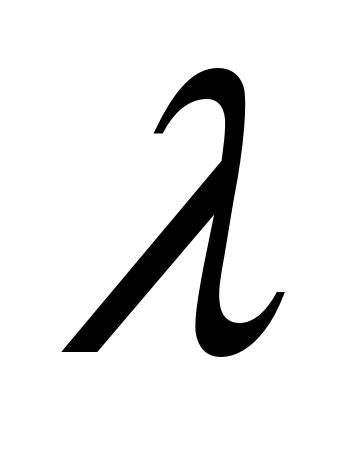 называется вектор называется вектор 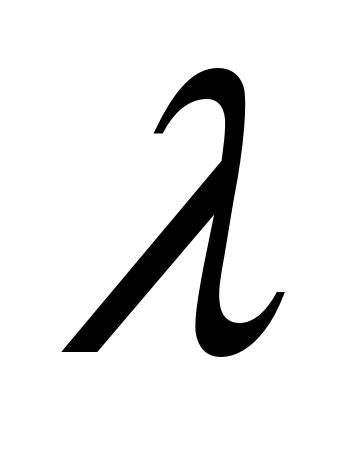 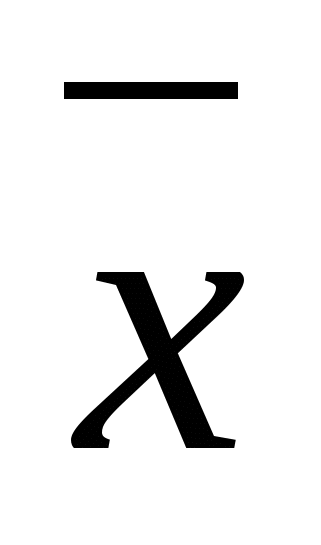 =( =(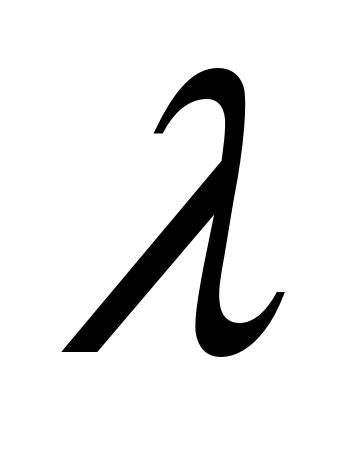 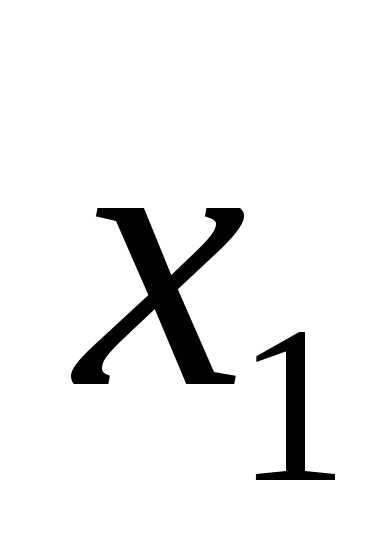 ; ;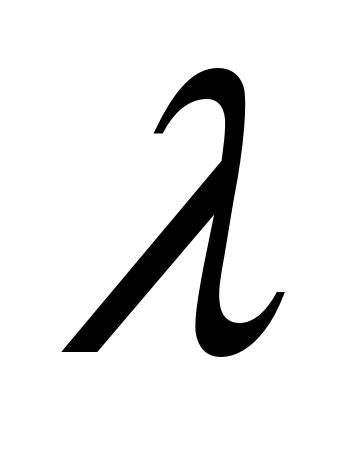 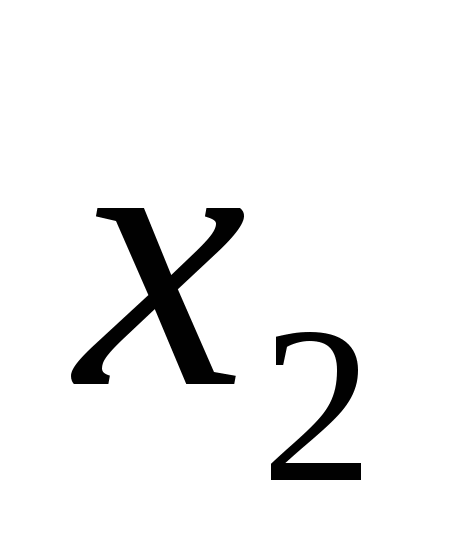 ;…; ;…;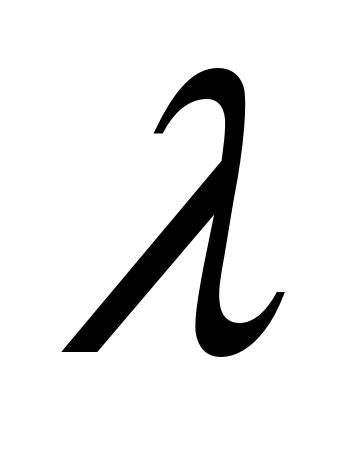 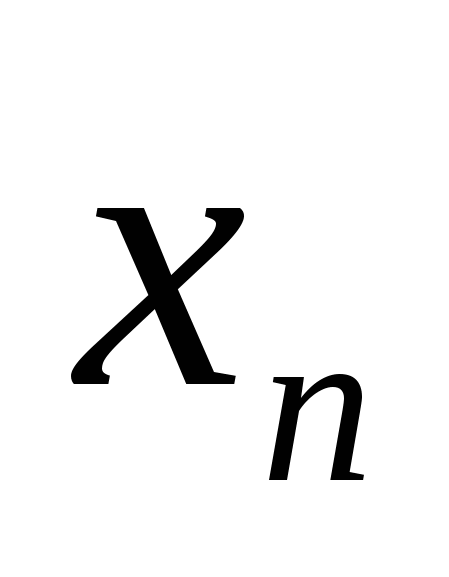 ), т. е. при умножении вектора на число каждая его координата умножается на это число. ), т. е. при умножении вектора на число каждая его координата умножается на это число.
Суммой векторов 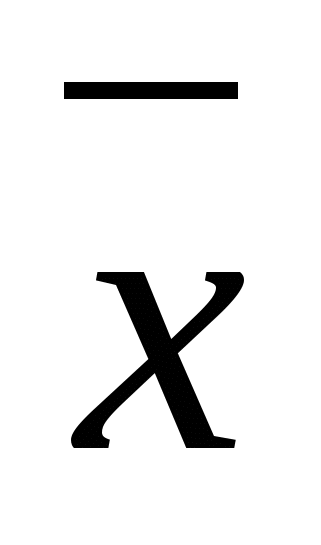 и и 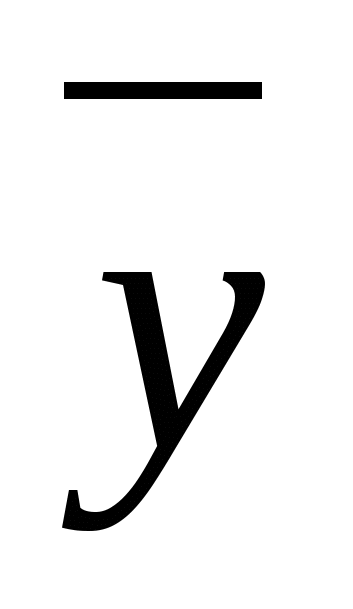 называется вектор называется вектор 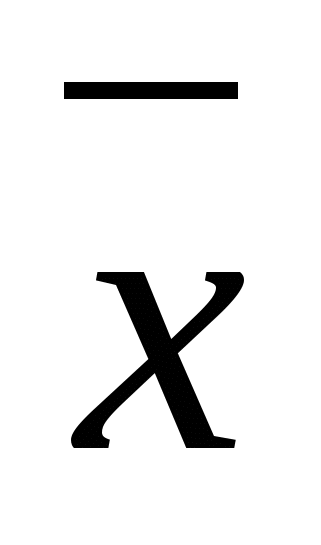 + +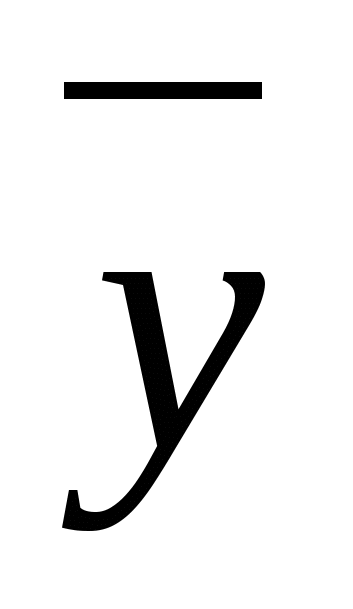 =( =(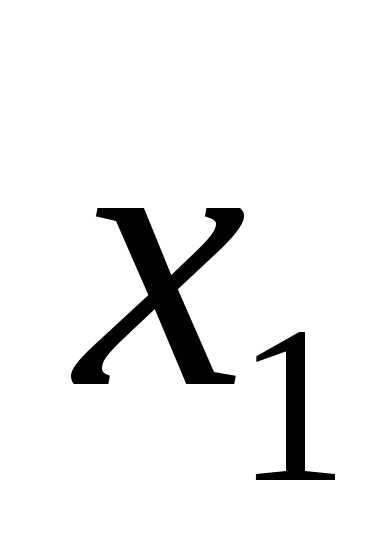 + +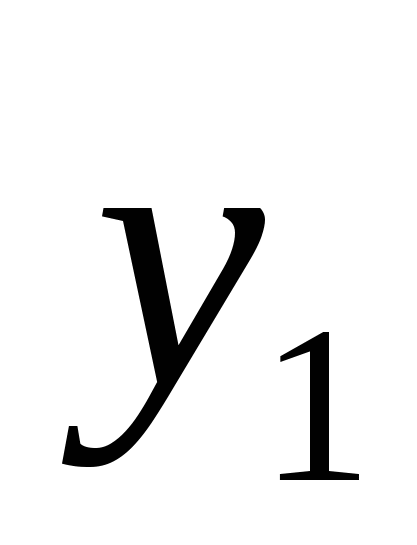 ; ;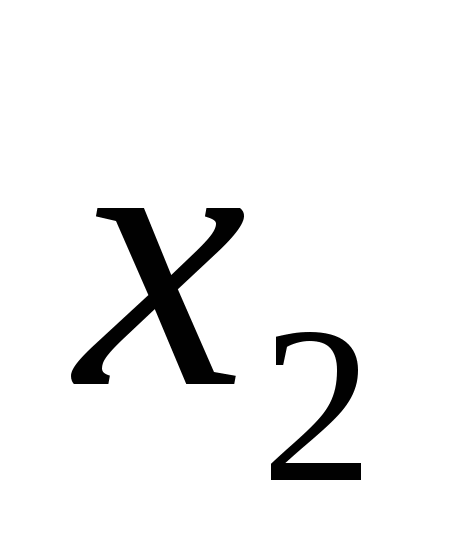 + +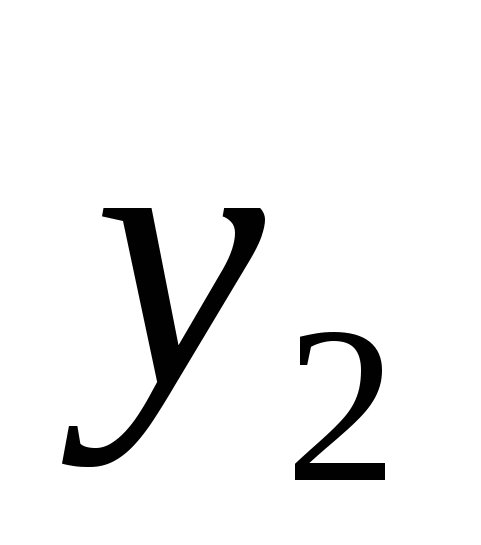 ;…; ;…;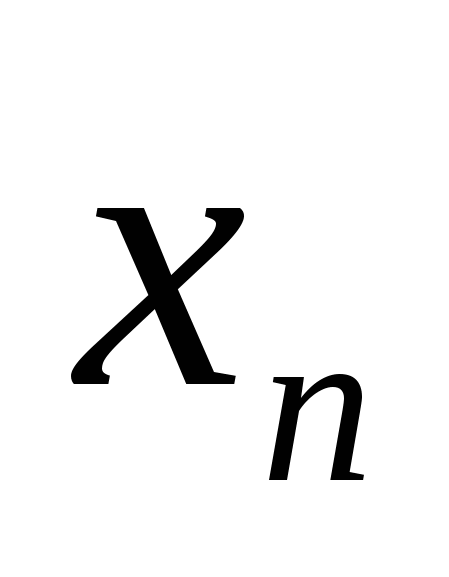 + +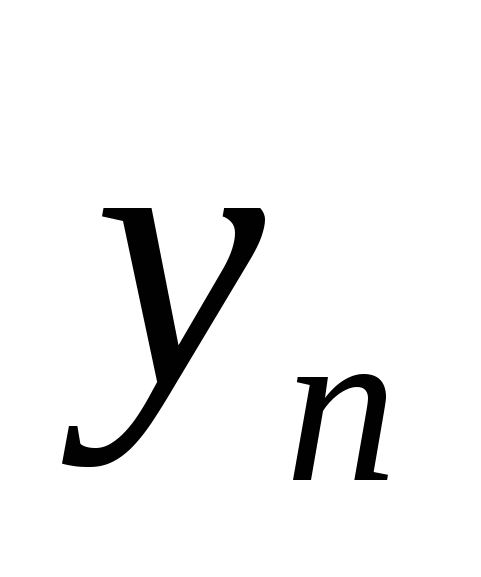 ),т. е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются. ),т. е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.
49)Линейной комбинацией векторов  , ,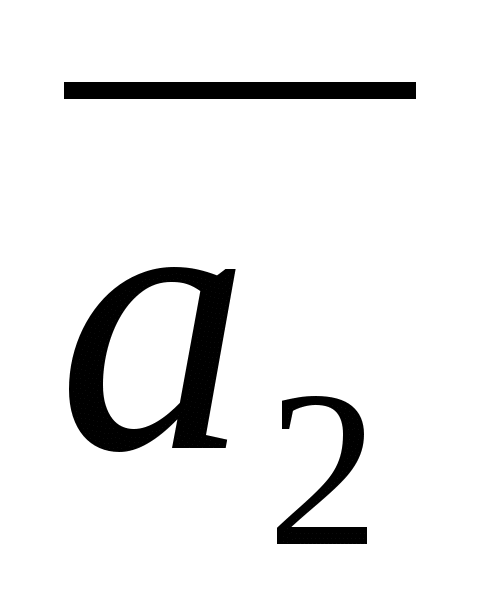 … …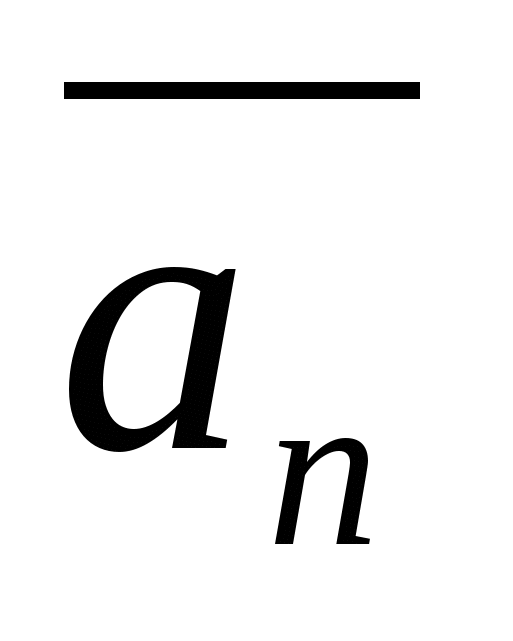 с коэффициентами с коэффициентами 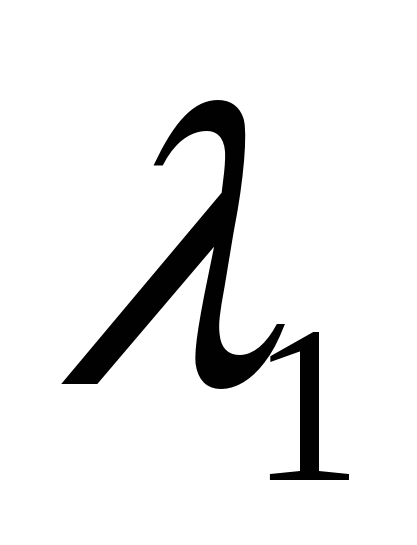 , ,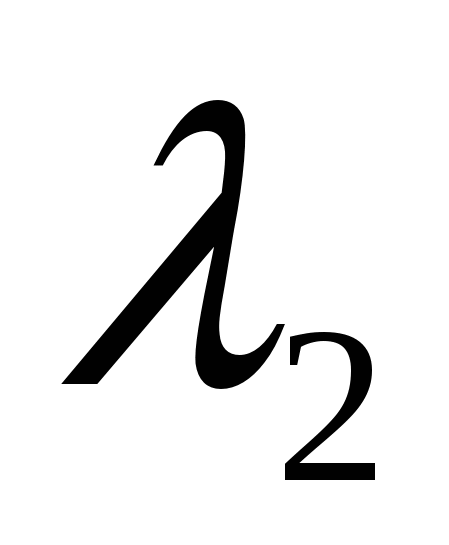 … …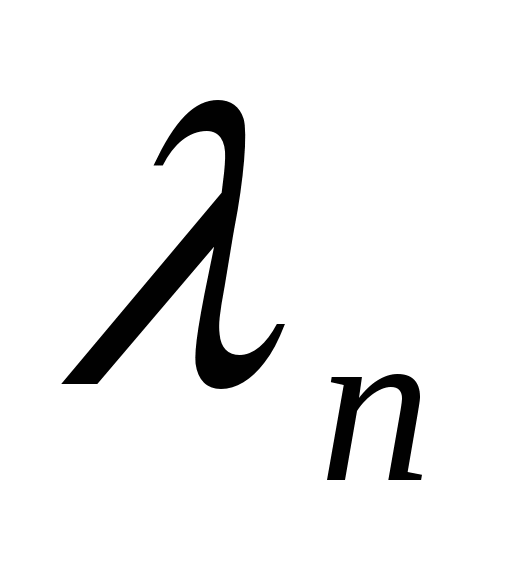 называется вектор называется вектор 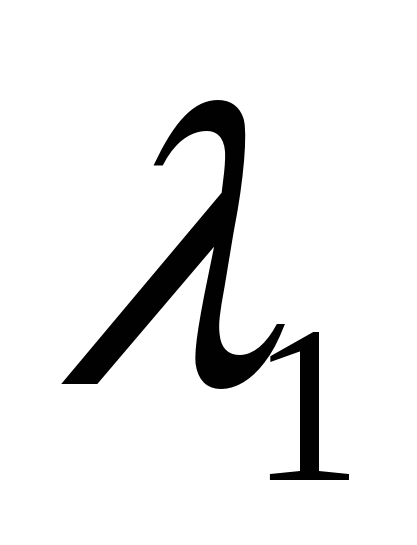  + +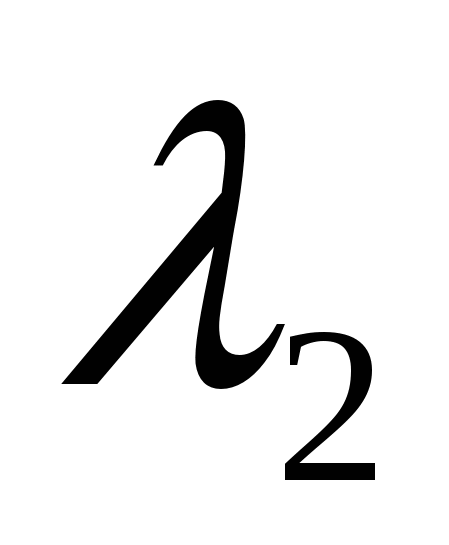 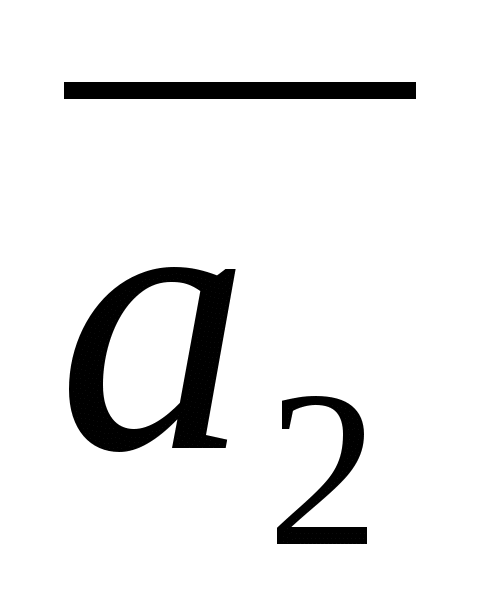 …+ …+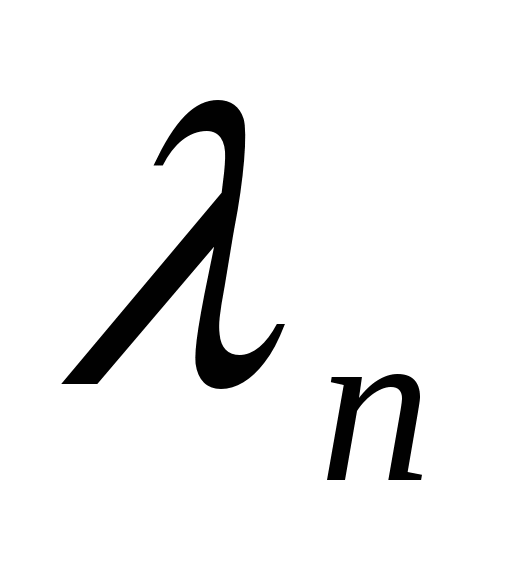 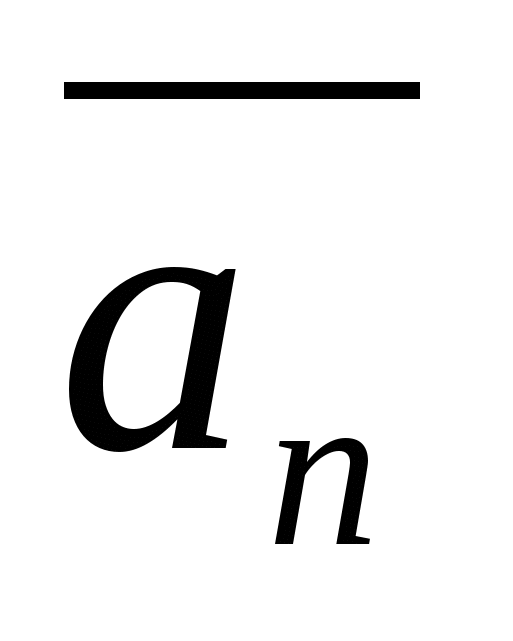 . Линейная комбинация векторов образуется из них с помощью операций умножения на число и сложения, следовательно, она также является вектором. По определению n-мерный вектор . Линейная комбинация векторов образуется из них с помощью операций умножения на число и сложения, следовательно, она также является вектором. По определению n-мерный вектор 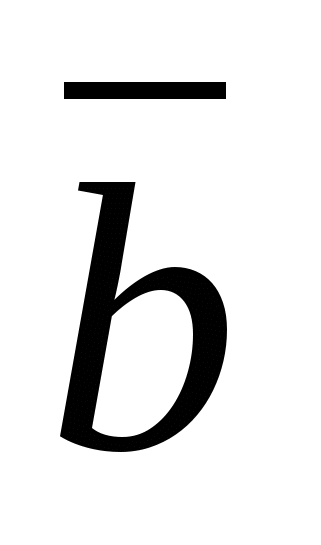 разлагается по системе векторов разлагается по системе векторов  , ,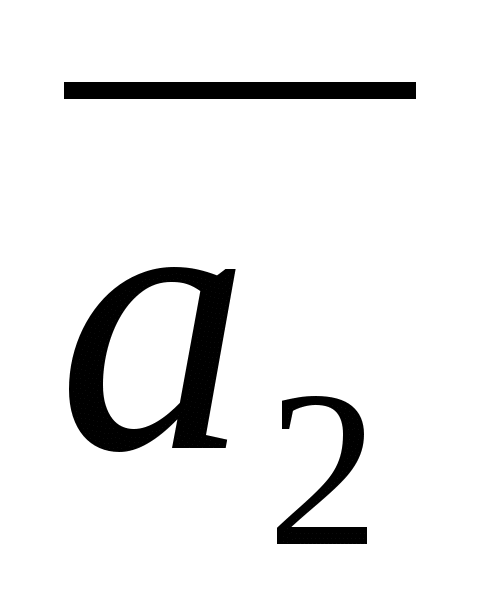 … …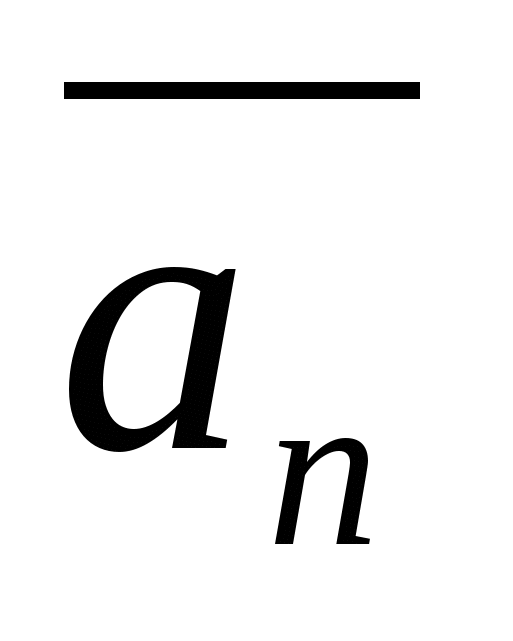 , если можно подобрать такие числа , если можно подобрать такие числа 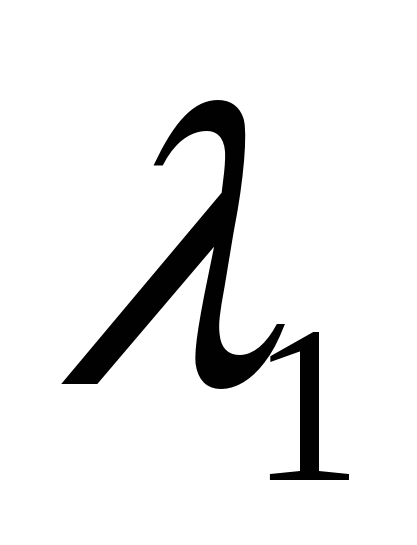 , ,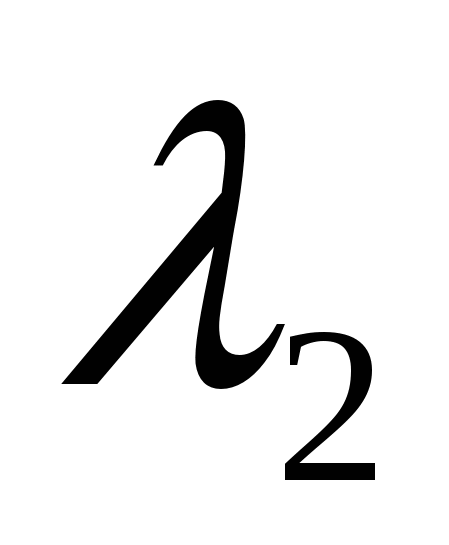 … …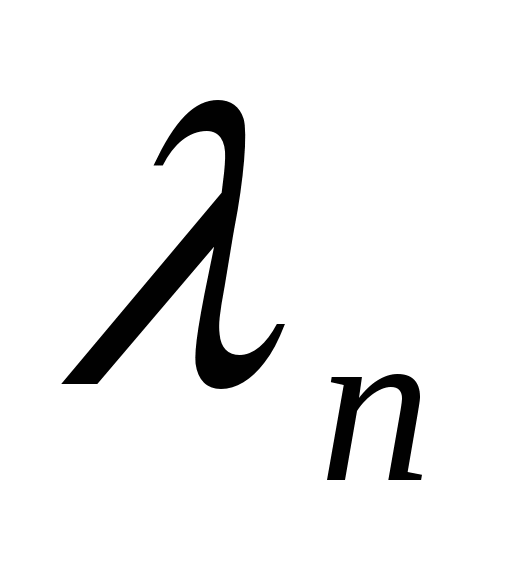 , что векторы , что векторы 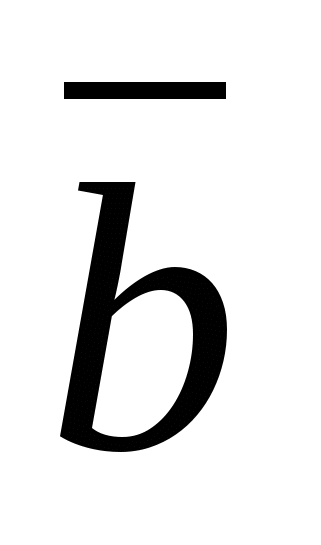 = =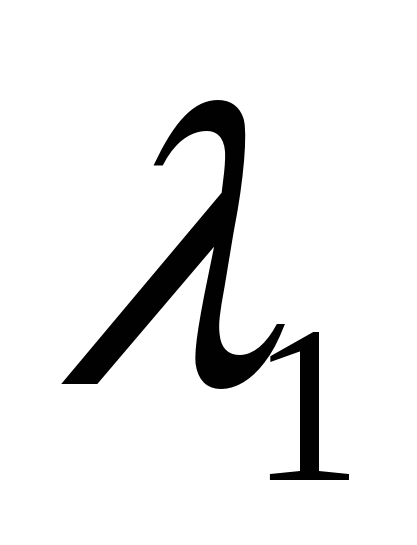  + +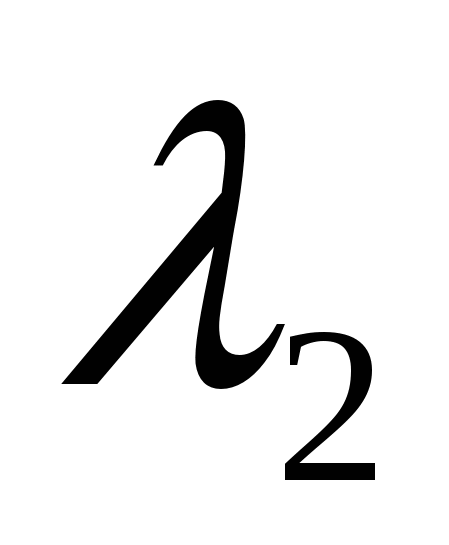 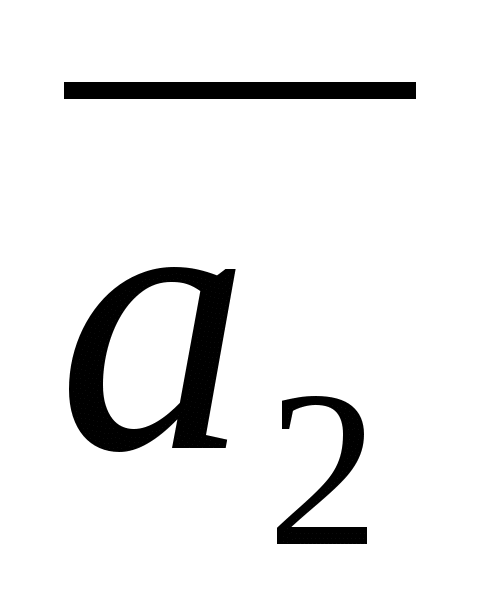 …+ …+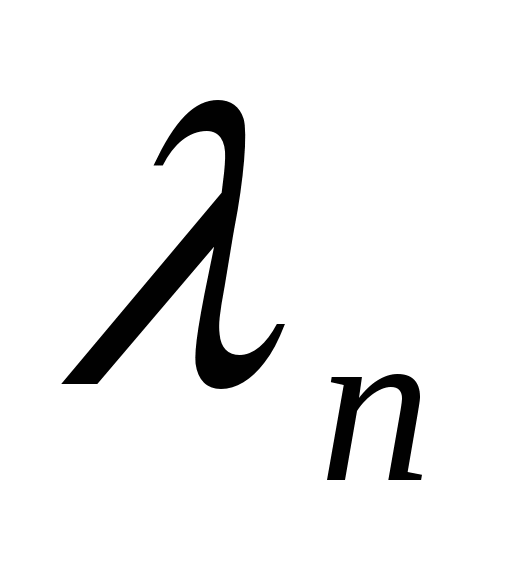 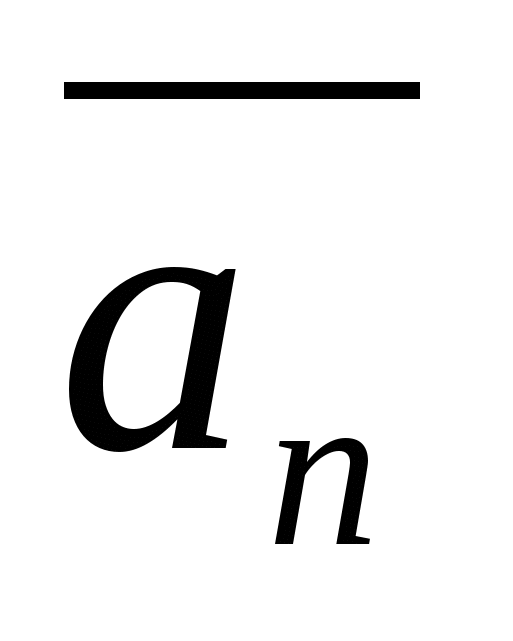 . Числа . Числа 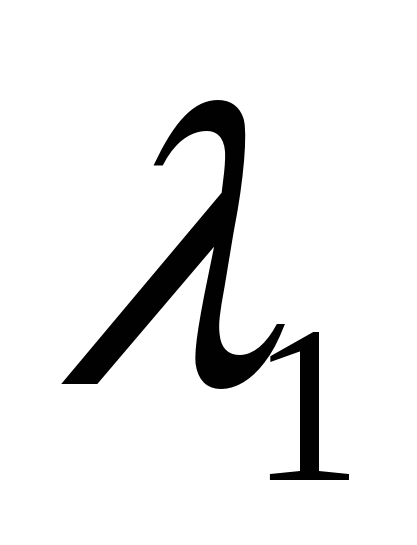 , ,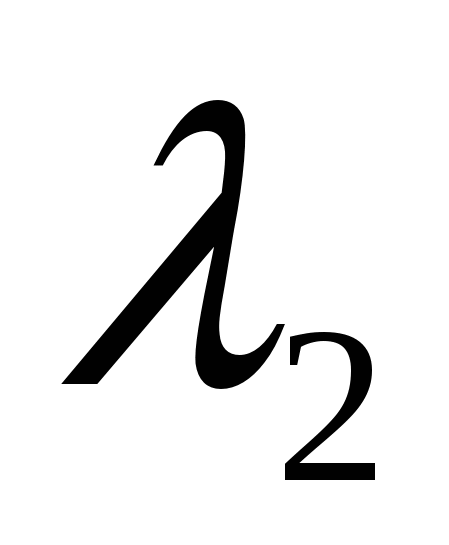 … …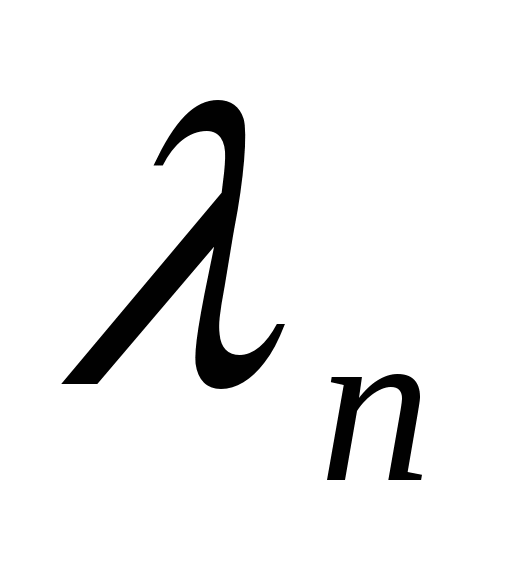 называются коэффициентами разложения. называются коэффициентами разложения.
Система векторов называется линейно зависимой, если из этих векторов можно составить нулевую (равную нулю) линейную комбинацию, т. е.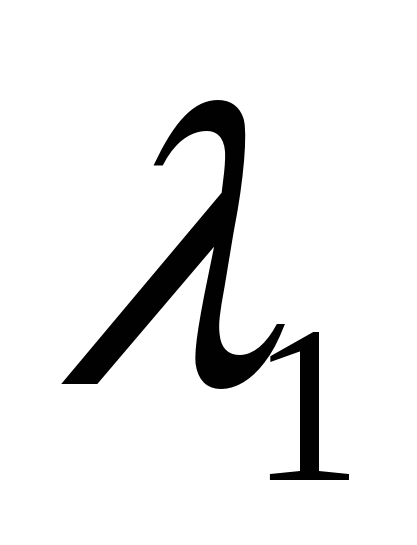  + +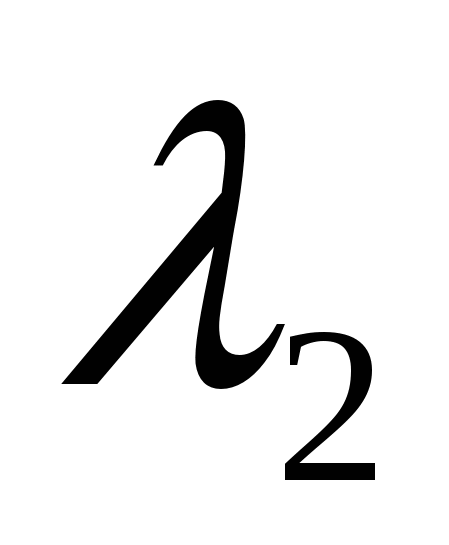 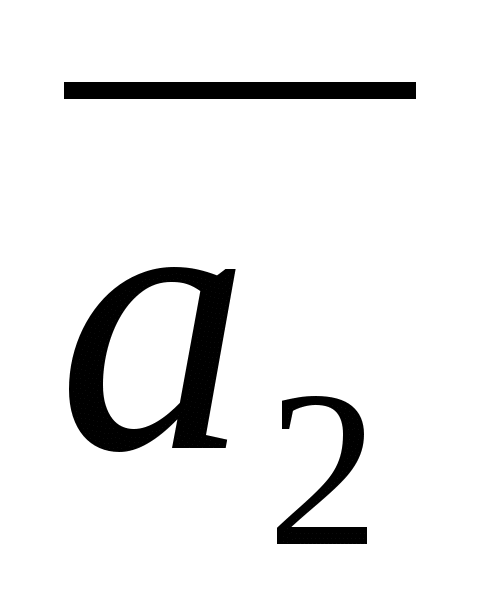 …+ …+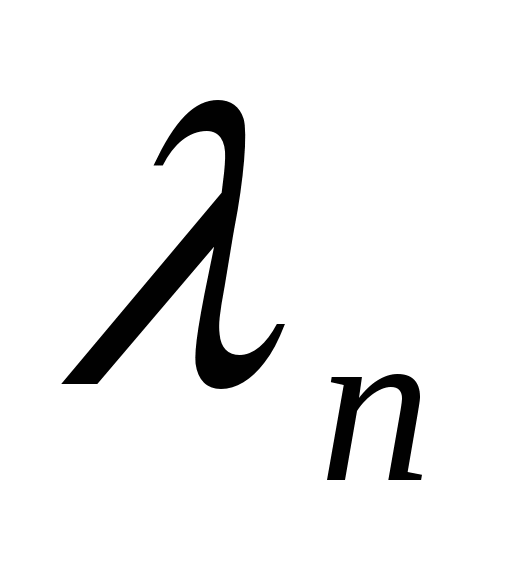 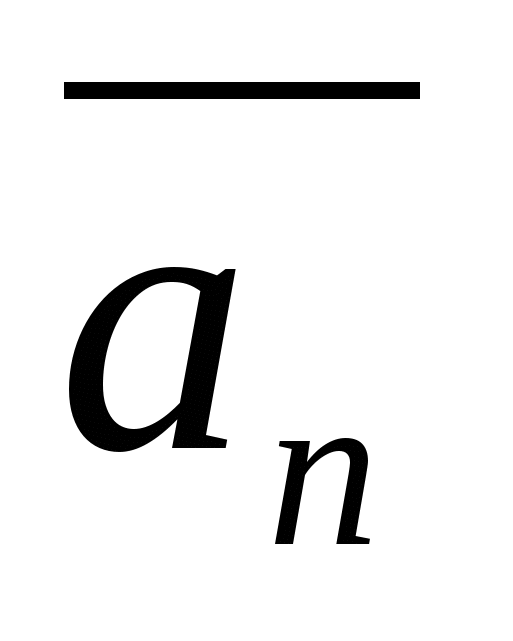 =0, причем хотя бы один из коэффициентов линейной комбинации отличен от нуля. В противном случае система векторов называется линейно независимой. =0, причем хотя бы один из коэффициентов линейной комбинации отличен от нуля. В противном случае система векторов называется линейно независимой.
50)Подпространство- такое подмножество Е данного пространства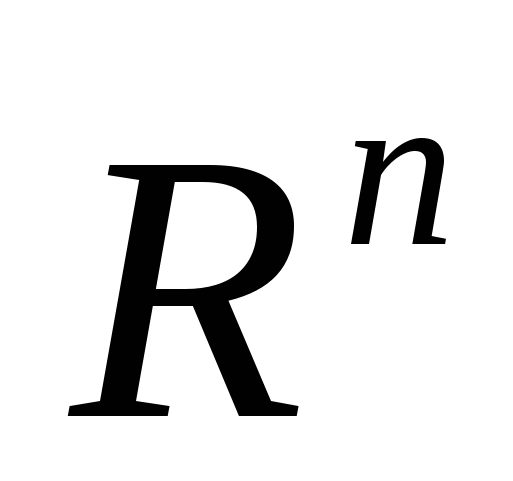 , которое само является пространством того же типа, что и , которое само является пространством того же типа, что и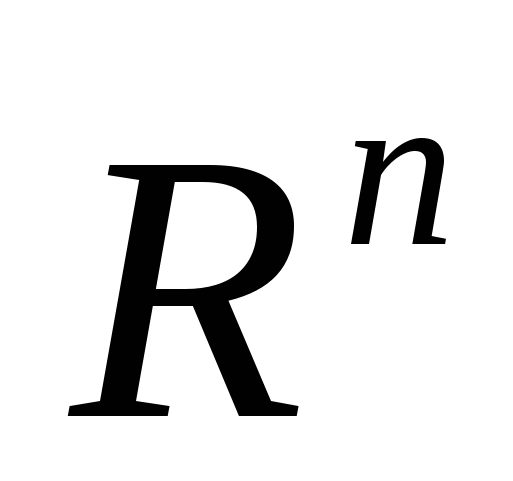 при усл. если при усл. если  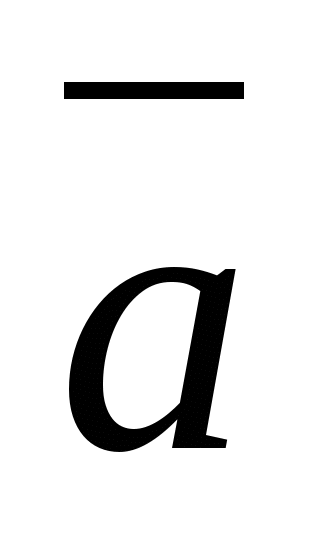 , ,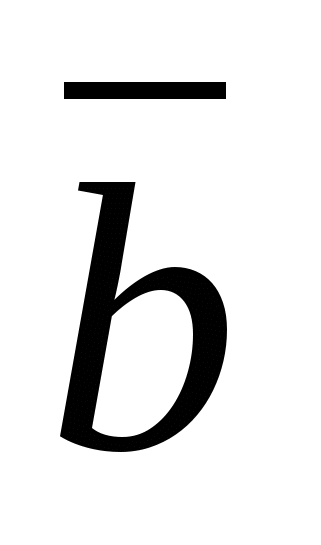  Е выполн. Е выполн. 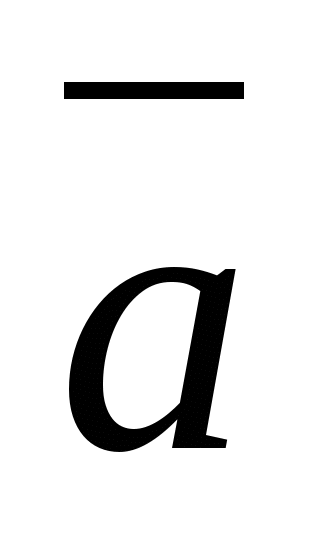 + +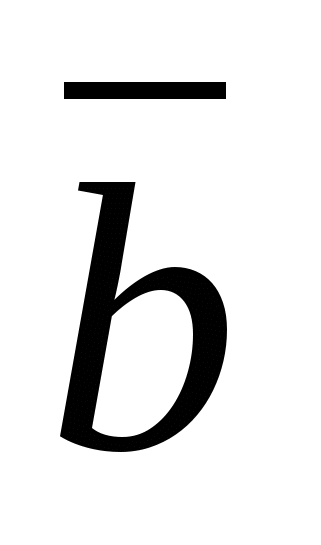  Е и Е и  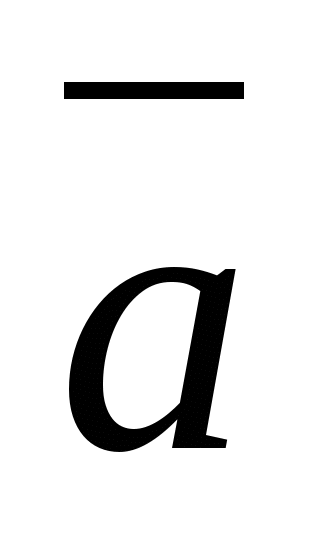 , ,  R выполн. R выполн.  * *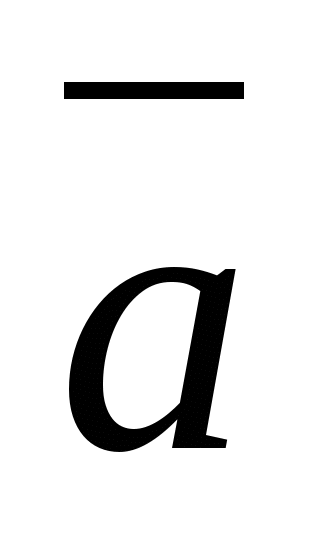  Е Е
51) Линейная оболочка подмножества а линейного пространства L — пересечение M всех подпространств L, содержащих а. Линейная оболочка L(а) состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из а. L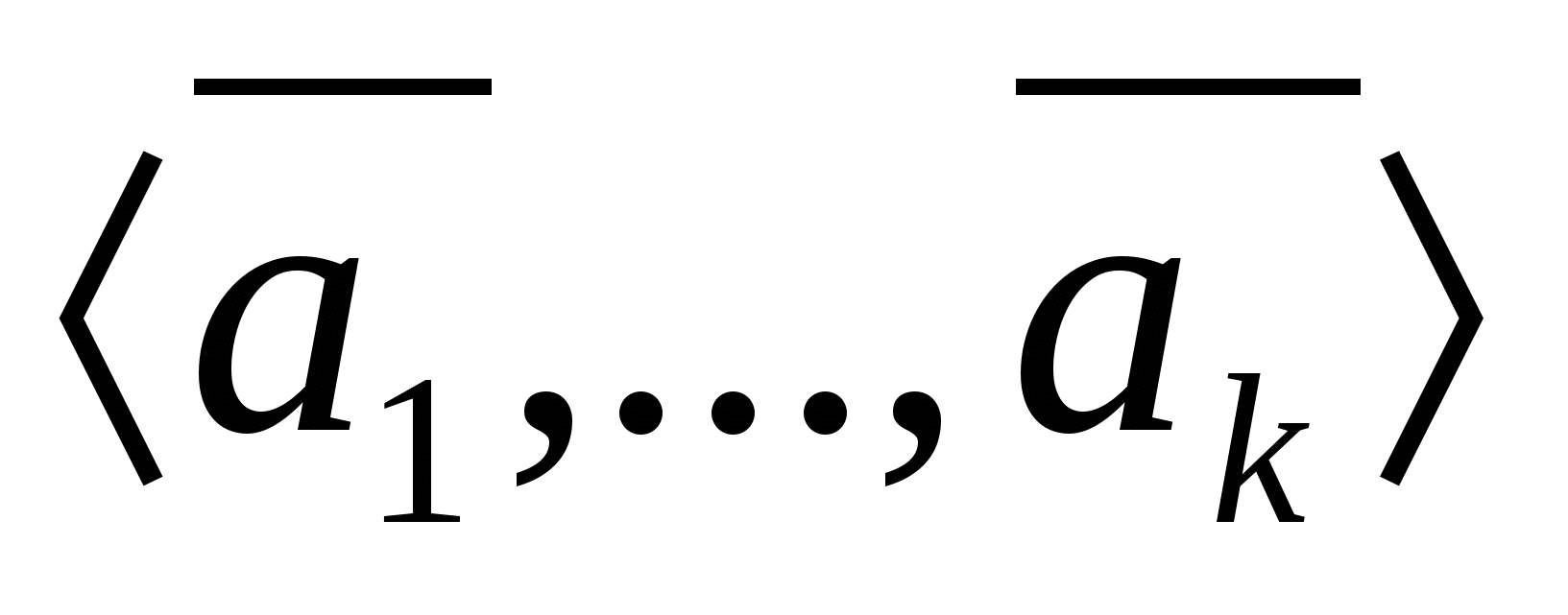 = =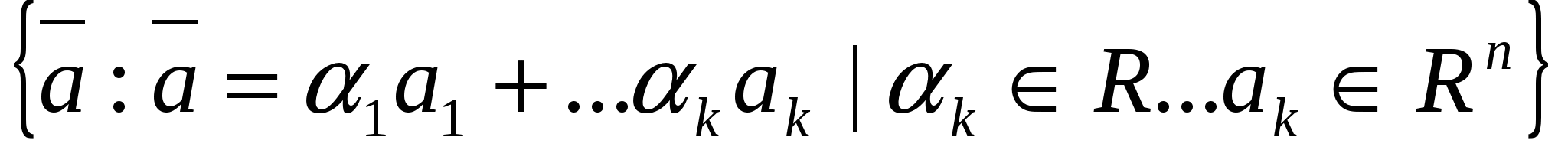 .Базисом является максимальное линейно независимое подмножество множества векторов на которое оболочка натянута.Чтобы наитии базис лин. оболочки нужно составить матрицу из вектор столбцов ( .Базисом является максимальное линейно независимое подмножество множества векторов на которое оболочка натянута.Чтобы наитии базис лин. оболочки нужно составить матрицу из вектор столбцов (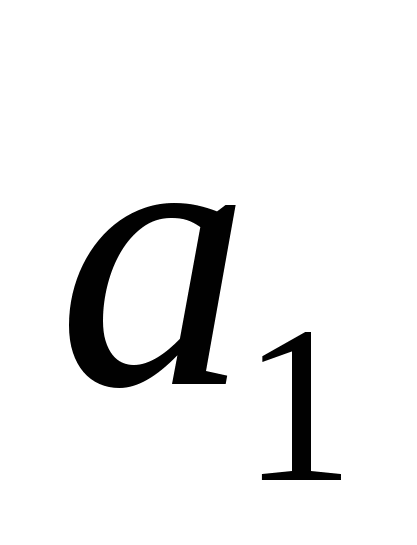 , ,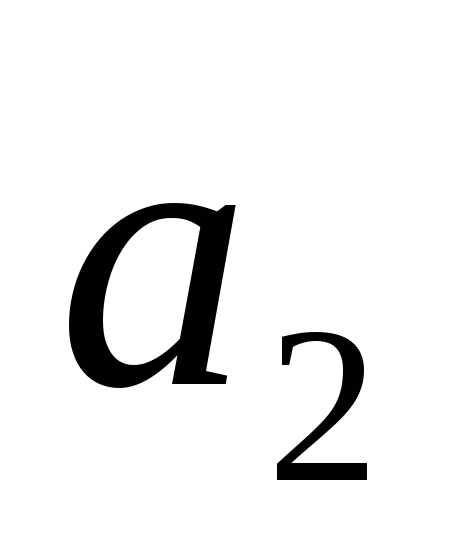 … …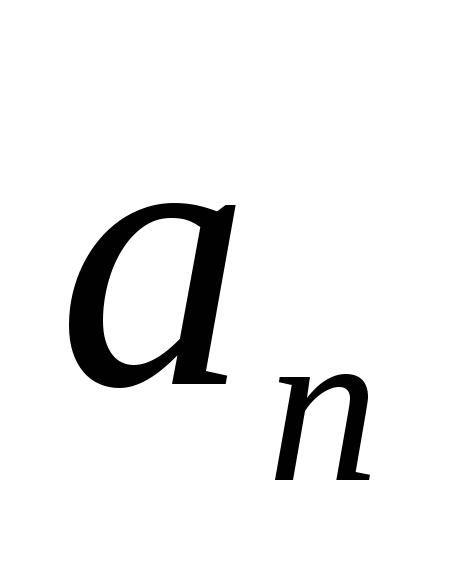 )Привести к ступенчатому виду и выделить главные столбцы. Векторы первоначально заданного мн-ва соотв. гл. столбцам образуют базис. )Привести к ступенчатому виду и выделить главные столбцы. Векторы первоначально заданного мн-ва соотв. гл. столбцам образуют базис. |
|
|
 Скачать 0.81 Mb.
Скачать 0.81 Mb.