Пирамида. Правильная пирамида. Усечённая пирамида.. Рассмотрим многоугольник А

• Название: Рассмотрим многоугольник А
• Дата: 09.06.2020
• Размер: 0.88 Mb.
• Имя файла: Пирамида. Правильная пирамида. Усечённая пирамида..doc
• Тип: Документы; #129177

Пирамида.

Рассмотрим многоугольник А₁А₂ … А_n и точку Р, не лежащую в плоскости этого многоугольника. Соединив точку Р отрезками с вершиной многоугольника, получим n треугольников (рисунок 1): РА₁А₂, РА₂А₃ …, РА_nА₁.

Многогранник, состоящий из n-угольника А₁А₂ … А_n и n треугольников РА₁А₂, РА₂А₃ …, РА_nА₁, называется пирамидой.

Многоугольник А₁А₂ … А_n – основание, треугольники РА₁А₂, РА₂А₃ …, РА_nА₁ – боковые грани. Точка Р – вершина, отрезки РА₁, РА₂ , …, РА_n – боковые ребра.

Обозначение: РА₁А₂ … А_n – n-угольная пирамида.

P вершина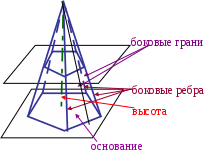


B_n

B₁ С

β B₂

A_n

H

A₁

α Е

A₂
РИС. 1
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания – высота (РН).

PE – апофема (высота боковой грани для правильной пирамиды)
Пирамида называется правильной, если её основание правильный многоугольник, а отрезок соединяющий вершину пирамиды с центром основания, является её высотой.

Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой (РЕ)
.



Центр правильного многоугольника – центр вписанной и описанной окружности. Тогда последнее определение можно сформулировать следующим образом: пирамида называется правильной, если ее основание — правильный многоугольник, а высота пересекает основание в центре вписанной и описанной окружности.
Свойства правильной пирамиды

1. 
   Все апофемы правильной пирамиды равны друг другу.
   
2. 
   Все боковые грани правильной пирамиды – равные равнобедренные треугольники.
   
3. 
   Все боковые ребра правильной пирамиды равны между собой.
   
4. 
   Высота пирамиды пересекает основание в центре вписанной и описанной окружности.
   
5. 
   Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
   

Теорема. Если пирамида пересечена плоскостью, параллельной основанию, то

1. 
   боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части;
   
2. 
   сечением этой плоскости является многоугольник, подобный основанию;
   
3. 
   площади сечения и основания относятся друг к другу как квадраты их расстояний от вершины.
   

Усеченная пирамида.

Проведем в пирамиде РА₁А₂ … А_n секущую плоскость , параллельную плоскости  основания пирамиды и пересекающую боковые ребра в точках В₁В₂,…, В_n (рисунок 1).

Плоскость  разбивает пирамиду на 2 многогранника.

Многогранник, гранями которого является n-угольники А₁А₂ …А_n и В₁В₂ …В_n (нижнее и верхнее основание), расположенные в параллельных плоскостях, и n-4^х угольников А₁А₂В₂В₁, А₂А₃В₃В₂, …, А_nА₁В₁В_n (боковые грани), называется усеченной пирамидой.

Отрезки А₁В₁, А₂В₂, …, А_nВ_n – боковые ребра.

Обозначение: А₁А₂ … А_nВ₁В₂ … В_n – усеченная пирамида

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой (СН).

Боковые грани усеченной пирамиды – трапеции.
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильного усечения пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами.

Тетраэдр.

Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DAB, DBC и DCA. Поверхность, составленная из четырех треугольников АВС, DAB, DBC и DCA, называется тетраэдром и обозначается DABC.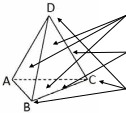



грани (4)

ребра (6)

вершины тетраэдра (4)


Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.

Одна из граней тетраэдра называется основанием, а три другие – боковыми гранями.

Сечения тетраэдра:

Тетраэдр имеет 4 грани, то его сечениями могут быть только

• 
  треугольники
  
• 
  четырехугольники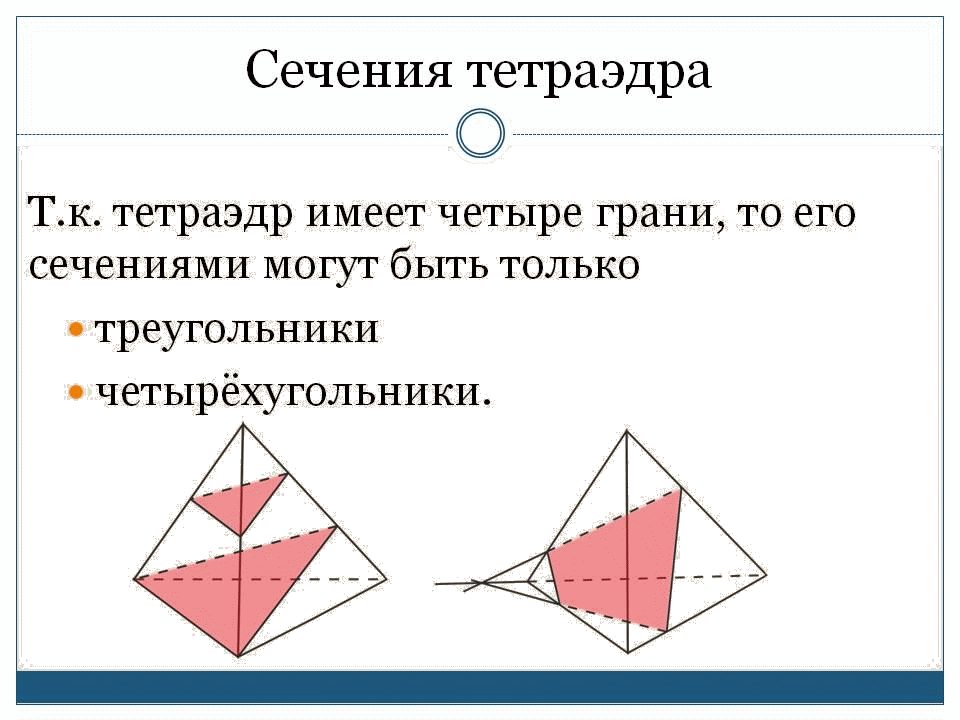
  

Правильный тетраэдр состоит из 4^х равносторонних треугольников. Каждая его вершина является вершиной 3^х треугольников,  сумма плоских углов при каждой вершине равна 180.

Симметрия в правильном тетраэдре:

Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер.         

Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.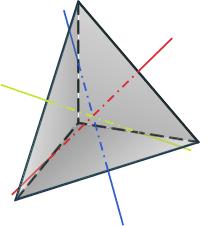



К правильным относятся 5 видов многогранникам:

1. 
   Куб
   
2. 
   Правильный тетраэдр
   
3. 
   Правильный октаэдр
   
4. 
   Правильный икосаэдр
   
5. 
   Правильный додекаэдр
   

С кубом и тетраэдром мы уже познакомились. Теперь рассмотрим остальные фигуры.

К уб состоит из 6 квадратов, в каждой вершине сходятся 3 квадрата,  сумма плоских углов равна 270.
Правильный октаэдр состоит из 8 равносторонних треугольников. Каждая его вершина является вершиной 4^х треугольников,  сумма плоских углов при каждой вершине равна 240.


Правильный икосаэдр состоит из 20 равносторонних треугольников. Каждая его вершина является вершиной 5^ти треугольников,  сумма плоских углов при каждой вершине равна 300.


Правильный додекаэдр состоит из 12 правильных пятиугольников. Каждая его вершина является вершиной 3^х правильных пятиугольников,  сумма плоских углов при каждой вершине равна 324.


Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и и несколько осей и плоскостей симметрии. Попробуйте подсчитать их число.
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней, а площадью боковой поверхности пирамиды - сумма площадей ее боковых граней.

S_полн = S_бок + S_осн

Площадь боковой поверхности правильной пирамиды равна ½ P · ℓ, где р – периметр, ℓ - апофема (высота)

Площадь боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.

Площадь боковой поверхности правильной усеченной пирамиды равна полусумме периметров оснований на апофему.

S бок = ½(Р+р) · ℓ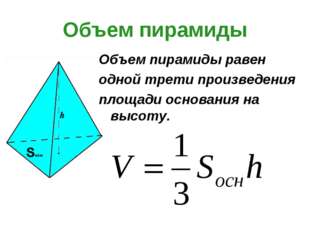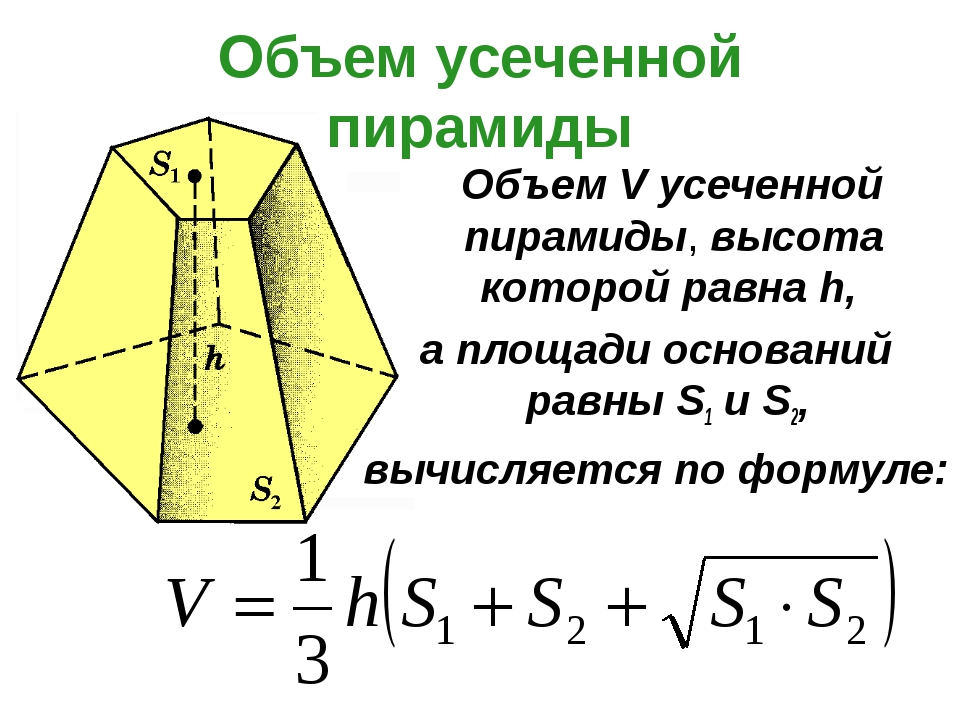






Вопросы для выявления уровня первичного запоминания

1. 
   Какая фигура называется пирамидой?
   

Ответ: Многогранник, состоящий из n-угольника А₁А₂ … А_n и n треугольников РА₁А₂, РА₂А₃ …, РА_nА₁, называется пирамидой.

2. 
   Какая фигура называется усеченной пирамидой?
   

Ответ: Многогранник, гранями которого является n-угольники А₁А₂ …А_n и В₁В₂ …В_n (нижнее и верхнее основание), расположенные в параллельных плоскостях, и n-4^х угольников А₁А₂В₂В₁, А₂А₃В₃В₂, …, А_nА₁В₁В_n (боковые грани), называется усеченной пирамидой.

3. 
   Какая формула выражает площадь полной поверхности пирамиды?
   

Ответ: S_полн = S_бок + S_осн

4. 
   Какая формула выражает площадь боковой поверхности правильной пирамиды?
   

Ответ: S_бок = ½ P · ℓ, где р – периметр, ℓ - апофема (высота)

5. 
   Какая формула выражает площадь боковой поверхности правильной усеченной пирамиды?
   

Ответ: S _бок = ½(Р+р) · ℓ
Задания.

1. 
   Сторона правильной треугольной пирамиды равна , боковое ребро равно 5. Найти высоту.
   
2. 
   Высота правильной треугольной пирамиды равна . Сторона треугольника основания пирамиды равна . Найти апофему.
   
3. 
   Высота правильной треугольной пирамиды равна . Сторона треугольника основания пирамиды равна . Найти боковое ребро.