ФокинА_1РГР. Равновесие механической системы

• Название: Равновесие механической системы
• Дата: 13.04.2021
• Размер: 0.63 Mb.
• Имя файла: ФокинА_1РГР.doc
• Тип: Решение; #194403

Расчетно-графическое задание по статике
РГР-1


РАВНОВЕСИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Группа
Студент Фокин А.
Оценка работы
Дата
Преподаватель

МОСКВА 2014г.

ЗАДАНИЕ
Определить реакции в точках А, В, С и характер изменения этих реакций в зависимости от направления действия силы Р1 (угла Р). Весом балок и трением в шарнирах пренебречь.

По варианту задания выбрана схема № 22 из приложения 1 и строка с исходными данными № 1 из таблицы приложения 2.
Решение
Рассмотрим схему, представленную на рисунке 1.

Механическая система состоит из балок АС и ВС, соединённых между собой цилиндрическим шарниром С. В точке А балка СА закрепляется под углом 90⁰ к стенке с помощью жёсткой заделки, в точке В – шарнирная подвижная опора N₁-N₂.

Система нагружена равномерно распределённой нагрузкой интенсивностью q, силой с моментом М, силой Р₁, приложенной к балке АС под углом β.

Необходимо определить реакции в точках А, В, С и характер изменения этих реакций в зависимости от направления действия силы Р₁ (угла β). Весом балок и трением в шарнирах пренебречь.
Вариант задания № 1

№ п/п	P1(H)	qmax (H/м)	q (H/m)	M (H-m)	a (m)	KE (m)	α°	γ°
1	1.5	1.0	4.8	1.0	1,2	0,6	60	45

Определить: R_ax(β), R_ay (β), R_a (β), R_cx (β), R_cy (β), R_C(β), R_B(β), M_A(β).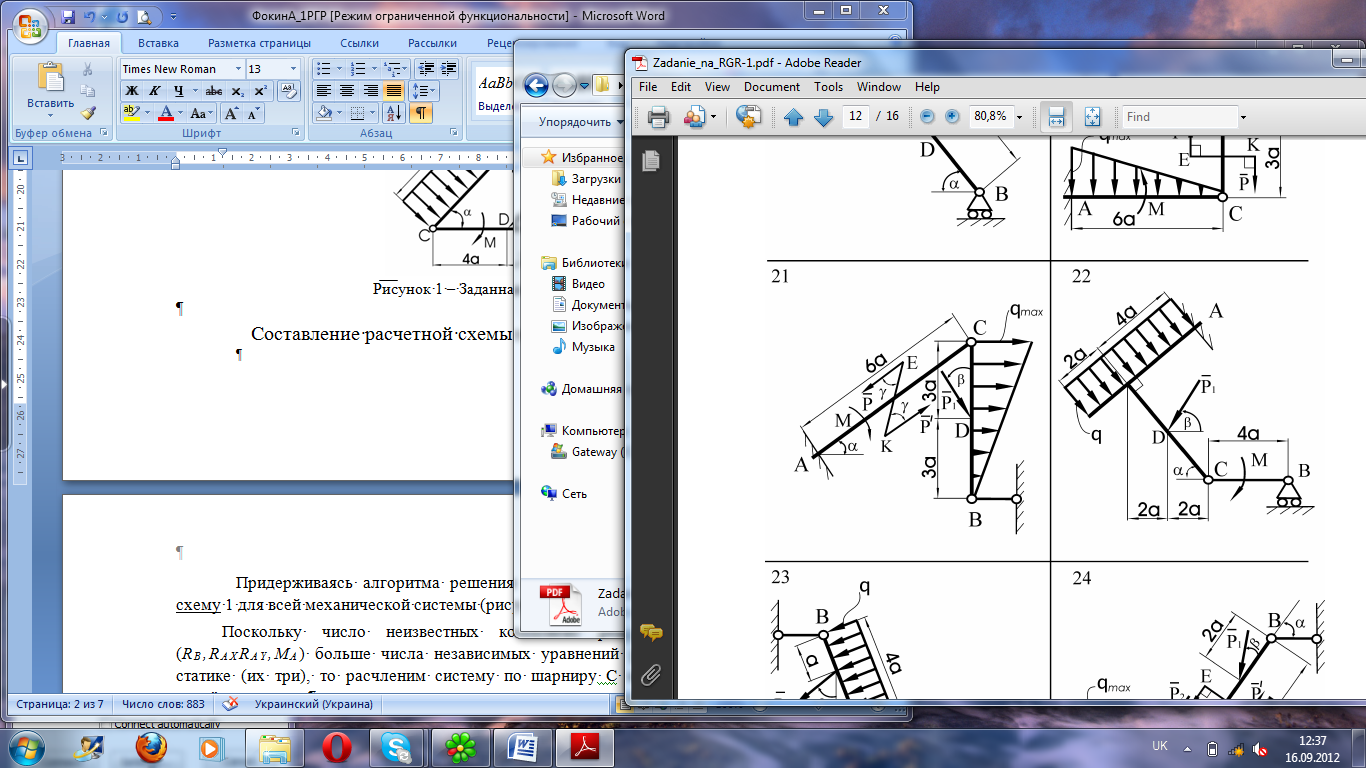


Рисунок 1 – Заданная схема № 22
Составление расчетной схемы и уравнений равновесия
Придерживаясь алгоритма решения задач статики, составим расчетную схему 1 для всей механической системы (рисунок 2).

Поскольку число неизвестных компонент реакций в этой схеме (R_B,R_AXR_AY,M_A) больше числа независимых уравнений равновесия в плоской статике (их три), то расчленим систему по шарниру С и составим две новые расчётные схемы.

Для каждой схемы определим систему сил и моментов, для которой выполняется система уравнений равновесия:

∑ F_KX = 0,

∑ F_KY = 0,

∑ М_C( F_k) = 0.

Моменты всех сил будем находить по теореме Вариньона, т.е. находить моменты для проекций этих сил на оси ОХ и ОY прямоугольной декартовой системы координат (расположение осей – традиционное).

Расчётная схема 2 (балка АС) показана на рисунке 3.


Y

A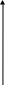



M_A

R_AX




Q


R_AY




Р₁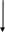








C

X


R_CX


R_CY

Рисунок 3 – Расчетная схема 2

Для балки АС:

1. 
   активные силовые факторы, действующие на балку АС:
   

• 
  равномерно распределённую нагрузку интенсивностью qзаменяем сосредоточенной силой Q(модуль силы Qравен Q= lq, где l– плечо под нагрузкой, точка приложения силы Q- точка О); момент силы Q относительно т. С;
  
• 
  сила Р₁;
  

2) связи:

• 
  в точке А - жёсткая заделка, реакция состоит из силы реакции (направление её заранее неизвестно, поэтому силу раскладываем на составляющие R_AX,R_AY) и моментом М_а;
  
• 
  в точке С – цилиндрический шарнир, составляющие реакции которого R'_Cx, R'_Cy(рис 4).
  

Уравнения равновесия для схемы 3 - АС:

4. 
   ∑ F_KX= -P_1X- R_CX- R_AX +Q_X=- P₁ sin(α+β) - R_CX- R_AX + 6qa*cosα = 0,
   
5. 
   ∑ F_KY= -Q_Y -P_1Y -R_CY- R_AY = - 6qa*sinα - P₁cos(α+β) -R_CY- R_AY = 0,
   
6. 
   ∑ M_C(F_k) = M_QX + M_P1Y- M_P1X+ M_QY + M_A =
   

= M_A – P₁6asin(α+β) + P₁6acos(α+β) + 3aQcosα+3aQsinα = 0.



Y

R_CY

M

R_B







C


X

B

R_CX

Рисунок 3 – Расчетная схема 2

Для балки ВС:

1. 
   активные силовые факторы:
   

• 
  момент М;
  

2) связи:

• 
  в точке В – шарнирная подвижная опора, реакция опоры направлена вверх;
  
• 
  в точке С – цилиндрический шарнир, составляющие реакции которого R_Cx, R_Cy(рис 4)
  

Уравнения равновесия для схемы 2 - BC (см. рис. 4):

1. 
   ∑ F_KX=R_CX =0,
   
2. 
   ∑ F_KY = R_CY +R_B =0,
   
3. 
   ∑ M_C(F_k) = –M -4aR_B= 0.
   

Решение системы уравнений
Перепишем систему уравнений, принимая во внимание, что R'_CX=R_CXи R'_CY=R_CY(модули этих сил равны) и учитывая, что
P_1X= P₁sin(α+β),

P_1Y=P₁cos(α+β),

Q_x=Qcosα,

Q_y=Qsinα.
Тогда имеем систему 6 уравнений :

R_CX =0,

R_CY +R_B =0,

–M -4aR_B= 0.

- P₁ sin(α+β) - R_CX- R_AX + 6qa*cosα = 0,

- 6qa*sinα - P₁ cos(α+β) -R_CY - R_AY = 0,

M_A – P₁6asin(α+β) + P₁6acos(α+β) + 3aq*cosα+3aq*sinα = 0.
После преобразований из уравнений (1), (3) получаем

R_CX= 0

R_AX=- P₁ sin(α+β) - R_CX+ 6qa*cosα

R_CY = - R_B

R_AY =- 6qa*sinα - P₁ cos(α+β) -R_CY

M_A = P₁6asin(α+β) - P₁6acos(α+β) - 3aq*cosα - 3aq*sinα

R_B = -М/4а
Полученные выражения представляют собой расчетные формулы, у которых в правой части равенства – заданные параметры (с учетом Q∙= 6q∙a), а в левой – искомые величины.

Результаты расчетов
Подсчет значений величин по полученным формулам проводим на компьютере в MS Excel.

Результаты расчетов сведены в таблицу 1, а их графическое представление приведено на рис.5.

Оценка величины реакции R_A и R_C приведена по формулам:
,

Исходные данные для расчета.

№ п/п	P1(H)	qmax (H/м)	q (H/m)	M (H-m)	a (m)	KE (m)	α°	β°
1	1.5	1.0	4.8	1.0	1,2	0,6	60	45

Таблица 1

β(°)		Rax	Ray	Ma	Rcx	Rcy	Rb
1	0	16	-31	-19,7	0	0,3	-0,3
2	30	15,8	-30,2	-12,8	0	0,3	-0,3
3	60	16	-29,5	-8,9	0	0,3	-0,3
4	90	16,5	-28,9	-8,9	0	0,3	-0,3
5	120	17,3	-28,7	-12,8	0	0,3	-0,3
6	150	18	-28,9	-19,7	0	0,3	-0,3
7	180	18,6	-29,5	-27,6	0	0,3	-0,3
8	210	18,8	-30,2	-34,4	0	0,3	-0,3
9	240	18,6	-31	-38,4	0	0,3	-0,3
10	270	18	-31,5	-38,4	0	0,3	-0,3
11	300	17,3	-31,7	-34,4	0	0,3	-0,3
12	330	16,5	-31,5	-27,6	0	0,3	-0,3
13	360	16	-31	-19,7	0	0,3	-0,3

По табличным данным были построим графики искомых параметров. По оси ОХ откладываются номера значений угла β (значения от 0 до 360 градусов).
График1 –Зависимость значений момента M_A от угла β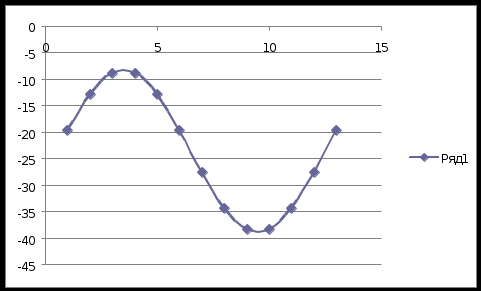



График 2 –Зависимости значений реакций и момента M_A от угла β



Рисунок 5

Ряд1 – Rax

Ряд2 – Ray

Ряд3 – Rcx

Ряд4 – Rcy

Ряд5 – Rb