Контрольная работа. Решение задач. Различные способы начисления процентов. Простой и сложный процент задачи 58 по теме Финансовая рента, задачи910 по теме Способы начисления амортизации
 Скачать 38.75 Kb. Скачать 38.75 Kb.
|
|
ТИПОВОЕ ЗАДАНИЕ ПО ДИСЦИПЛИНЕ «ФИНАНСОВАЯ МАТЕМАТИКА» ДЛЯ ЗАОЧНИКОВ (задачи №№1-2 по теме «Ссудный и учетный процент»; задачи №№ 3-4 по теме «Различные способы начисления процентов. Простой и сложный процент»; задачи №№ 5-8 по теме «Финансовая рента», задачи№№9-10 – по теме «Способы начисления амортизации») Вариант 8. Задача 1. X=30000; n=3; d=15. Задача 2. P= 80000; n=4; i= 20. Задача 3. Y=60000; n=5; ic=18. Задача 4. j1= 24; j2=18; j2=16. Задачи 5-8. R = 50 тыс. руб. n = 10 лет. j = 10% Задачи 9-10. С = 1 млн. руб. Спи = 6 лет. Q1= 50 тыс.ед. Q2= 70 тыс.ед. Q3= 90 тыс.ед. Q4= 100 тыс.ед. Q5=140тыс.ед. Q6 = 150 тыс.ед. Задача 1. Вексель номиналом X рублей учтен в банке за n месяцев до погашения. Определите сумму, полученную владельцем векселя, если ставка учетного процента равен d (% годовых). Решение: x (номинал векселя)=30000 руб.; n(период до погашения)=3 мес.; d(ставка учетного процента)=15%. Определим сумму, полученную по векселю по формуле простого процента: S=P (1+nd) или при неполном сроке лет: S= P* (1+ 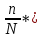 d) d) где: S = будущая сумма, P = номинал векселя (первоначальная сумма), n = срок оплаты; d процентная ставка, n = срок оплаты – 3 месяца = 90 дней N – количество дней в году = 365 Сумма, полученная по векселю составит: S = 30000 (1+ 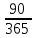 * 0,15) = 31109,6 руб. * 0,15) = 31109,6 руб.Ответ: Владелец векселя получит сумму в размере 31109,6 руб. Задача 2. Покупатель приобретает в магазине товар по цене P рублей. На всю сумму он берет кредит, который должен быть возвращен в течение n лет. Определите всю сумму долга, при условии, что ставка простого ссудного процента равна i (% годовых). Решение: P (сумма кредита – первоначальная сумма)= 80000 руб.; N (срок кредита)=4 года; I (процент по кредиту)= 20% Сумму долга определяем по формуле простого процента: S=P (1+nd) где: S = сумма долга – будущая сумма, P = сумма кредита – первоначальная сумма, n = срок кредита; d ставка ссудного процента. S=80000*(1+0,2*4) = 144000 руб. Ответ: Сумма долга составит 144000 руб. Задача 3. Какой величины достигнет размер долга, равный Y руб., через n лет при росте по сложной процентной ставке iс (% годовых)? Решение: Y (размер долга - первоначальный)=60000 руб.; n (период)=5 лет; ic (процентная ставка сложная)=18% Сумму будущего долга определяем по формуле сложного процента: S=Y (1+ic)n где: S = сумма будущего долга, Y = сумма кредита – первоначальная сумма, n = срок кредита; ic сложная процентная ставка. S=60000 (1+0,18)5 = 137265,5 руб. Ответ: Сумма будущего долга составит 137265,5 руб. Задача 4. Рассчитайте эффективные процентные ставки по депозитным договорам и определите наиболее выгодный процент для вкладчика: а) годовой процент j1(%), периодичность начисления один раз в полгода; б) годовой процент j2(%, периодичность начисления один раз в квартал; в) годовой процент j3(%), периодичность начисления один раз в год. Решение: j1(годовой процент с периодичностью 1 раз в полгода)= 24%; j2(годовой процент с периодичностью 1 раз в квартал)=18%; j3(годовой процент с периодичностью 1 раз в год)=16%. Годовую эффективную ставку процента определим по формуле: iэ = 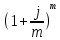 – 1 – 1где: iэ – эффективная годовая процентная ставка; m – количество начислений в году; j 1,2,3– годовой процент (номинальная процентная ставка). iэ1=(1+ 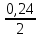 )2 – 1= 0,2544 = 25,44%; )2 – 1= 0,2544 = 25,44%;iэ2=(1+  )4 – 1= 0,1925 = 19,25%; )4 – 1= 0,1925 = 19,25%;iэ3=(1+  )1 – 1= 0,16= 16%; )1 – 1= 0,16= 16%;Ответ: Эффективная процентная ставка iэ1=25,44%, iэ2=19,25%, iэ3=16%. Эффективная ставка процента показывает реальный доход инвестора от вклада или эффективность роста денег на счету вкладчика, следовательно наиболее выгодным процентом будет являться iэ1=25,44% Задача 5. На счет в банке в течение n лет ежегодно (в начале каждого года) вносится сумма в размере R руб., на которую в конце года 1 раз в год начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада). Решение: R (вносимая в банк сумма)= 50 тыс. руб. n = (период вложения средств)= 10 лет j (номинальная процентная ставка) =10% Так как период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента. Сумма всех взносов с начисленными процентами будет равна: FVA = R  где: FVA – наращенная сумма – сумма всех взносов с начисленными процентами; R – вносимая в банк сумма; j – номинальная процентная ставка; n – период вложения средств. FVA = 50000 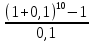 = 796871,2 руб. = 796871,2 руб.Сумма взносов в течение 10 лет составит: P = n * R P =10 * 50000 = 500000 руб. Сумма начисленных процентов будет равна: I = FVA – P I = 796871,2 – 500000 = 296871,2 руб. Ответ: Доход владельца счета за весь срок ренты составит 296871,2 руб. Задача 6. На счет в банке в течение n лет ежегодно (в начале каждого года) вносится сумма в размере R руб, на которую ежеквартально (в конце каждого квартала) начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада). Решение: R (вносимая в банк сумма)= 50 тыс. руб. n = (период вложения средств)= 10 лет j (номинальная процентная ставка) =10% Взносы начисляются в начале периода ренты, значит аннуитет пренумерандо Рассчитать будущую стоимость аннуитета пренумерандо можно воспользовавшись следующей формулой. FVA = 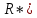  * (1+j/m) * (1+j/m) где: FVA – наращенная сумма – сумма всех взносов с начисленными процентами; R – вносимая в банк сумма; j – номинальная процентная ставка; n – период вложения средств. FVA = 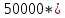 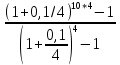 * (1+0,1/4) = 50000* * (1+0,1/4) = 50000*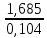 *1,025 = 831876,7 руб. *1,025 = 831876,7 руб.Сумма взносов в течение 10 лет составит: P = n * R P =10 * 50000 = 500000 руб. Сумма начисленных процентов будет равна: I = FVA – P I = 831876,7 – 500000 = 331876,7 руб. Ответ: Доход владельца счета за весь срок ренты составит 331876,7 руб. Задача 7. На счет в банке в течение n лет ежегодно вносится сумма в размере R руб, но взносы поступают ежеквартально, равными частями (т.е. R/4). На размер годовых поступлений R ежеквартально начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада). Решение: Задача 8. На счет в банке в течение n лет ежегодно вносится сумма в размере R руб, но взносы поступают ежеквартально, равными частями (т.е. R/4). На размер годовых поступлений R ежемесячно начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада) FVA =   Задача 9. Определить годовую норму амортизации и годовую сумму амортизационных отчислений для каждого года срока полезного использования основных средств, используя способ списания стоимости по сумме числе лет срока полезного использования, если известна первоначальная стоимость объекта основных средств С и срок его полезного использования Cпи. Решение: С (первоначальная стоимость основных средств) = 1 млн. руб. Спи (срок полезного использования) = 6 лет. Q1(объем продукции)= 50 тыс.ед. Q2(объем продукции)= 70 тыс.ед. Q3(объем продукции)= 90 тыс.ед. Q4(объем продукции)= 100 тыс.ед. Q5(объем продукции)=140 тыс.ед. Q6 (объем продукции)= 150 тыс.ед. Норма амортизации – это установленный в процентах от стоимости размер амортизации за определенный период времени по конкретному виду основных фондов. Рассчитывается по формуле: Na = 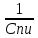 *100 *100где: Na – норма амортизационных отчислений; Спи – срок полезного использования. Na = 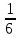 *100 = 16,66% *100 = 16,66%Сумму амортизации за каждый год использования основного средства по способу списания стоимости по сумме числе лет срока полезного использования рассчитывается по формуле: Аi = 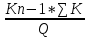 где: Аi – годовая сумма амортизационных отчислений для каждого года; Kn-1 – количество лет, оставшихся до конца срока полезного использования основного средства; ∑K – сумма чисел лет срока полезного использования, ед. С – первоначальная сумма основных средств. Сумма чисел лет срока полезного использования основных средств равна: 1 + 2 + 3 + 4 + 5 + 6= 21 год. В первый год эксплуатации основных средств годовая сумма амортизации составит: 6: 21 × 1000000 руб. = 285714,3 руб. Во второй год эксплуатации основных средств годовая сумма амортизации составит: 5 : 21 × 1000000 руб. = 238095,2 руб. В третий год эксплуатации основных средств сумма амортизации составит: 4: 21 × 1000000 руб. = 190476,2 руб. В четвертый год эксплуатации основных средств сумма амортизации составит: 3: 21 × 1000000 руб. = 142857,1 руб. В пятый год эксплуатации основных средств сумма амортизации составит: 2: 21 × 1000000 руб. = 95238,1 руб. В шестой год эксплуатации основных средств сумма амортизации составит: 1: 21 × 1000000 руб. = 47619,05 руб. Ответ: Норма амортизации составляет 16,66%. Годовая сумма амортизационных отчислений составляет по годам за 6 лет: 285714,3 руб., 238095,2 руб., 190476,2 руб., 142857,1 руб., 95238,1 руб., 47619,05 руб. соответственно. Задача 10. Определить годовую норму амортизации и годовую сумму амортизационных отчислений для каждого года срока полезного использования основных средств, используя способ списания стоимости пропорционально объему продукции, если известна первоначальная стоимость объекта основных средств С, срок его полезного использования Cпи, а также объемы произведенной продукции Q по годам (Q1, Q2, Q3 … и т.д.) Решение: С (первоначальная стоимость основных средств) = 1 млн. руб. Спи (срок полезного использования) = 6 лет. Q1(объем продукции)= 50 тыс.ед. Q2(объем продукции)= 70 тыс.ед. Q3(объем продукции)= 90 тыс.ед. Q4(объем продукции)= 100 тыс.ед. Q5(объем продукции)=140 тыс.ед. Q6 (объем продукции)= 150 тыс.ед. Норма амортизации – это установленный в процентах от стоимости размер амортизации за определенный период времени по конкретному виду основных фондов. Рассчитывается по формуле: Na =  *100 *100где: Na – норма амортизационных отчислений; Спи – срок полезного использования. Na =  *100 = 16,66% *100 = 16,66%Сумму амортизации за каждый год использования основного средства по способу списания стоимости пропорционально объему продукции рассчитывается по формуле: Аi =  где: Аi – годовая сумма амортизационных отчислений для каждого года; С – первоначальная сумма основных средств; Q – объем произведенной продукции за весь срок полезного использования. Рассчитаем общий объем произведенной продукции за весь срок полезного использования, за 6 лет: Q = Q1+Q2+Q3+Q4+Q5+Q6 Q = 50 + 70 + 90 + 100 + 140 + 150 = 600 тыс. ед. А (1-й год) =  = 83333,33 руб. = 83333,33 руб.А (2-й год) =  = 116666,7 руб. = 116666,7 руб.А (3-й год) = 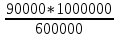 = 150000 руб. = 150000 руб.А (4-й год) = 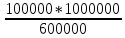 = 166666,7 руб. = 166666,7 руб.А (5-й год) =  = 233333,3 руб. = 233333,3 руб.А (6-й год) =  = 250000 руб. = 250000 руб.Ответ: Норма амортизации составляет 16,66%. Годовая сумма амортизационных отчислений составляет по годам за 6 лет: 83333,33 руб., 116666,7 руб., 150000 руб., 166666,7 руб., 233333,3 руб., 250000 руб. соответственно. |
