коллоквиум по физике. Коллобокиум. Разложение радиус вектора по координатным векторам

Название	Разложение радиус вектора по координатным векторам
Анкор	коллоквиум по физике
Дата	12.01.2021
Размер	0.65 Mb.
Формат файла
Имя файла	Коллобокиум.docx
Тип	Документы #167304

Коллоквиум

1.Радиус вектор- вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Разложение радиус вектора по координатным векторам:

Координатные векторы направленны вдоль осей координат, и их модули равны 1: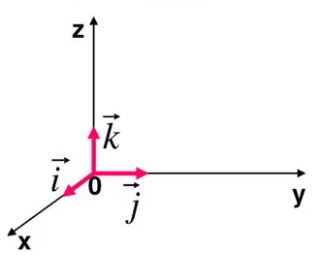

+ k (0;0;1); любой вектор d можно разложить единственным образом по координатным векторам:

Модуль радиус вектора:

2. Вектор перемещения — это направленный отрезок, проведенный из начального положения материальной точки в ее конечное положение. Перемещением характеризуется изменение радиус-вектора точки.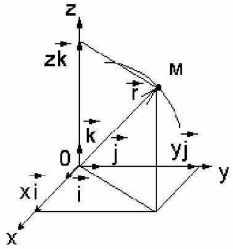

Модуль вектора перемещения:

3. Средняя скорость— это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден

; м/с; метр в секунду

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения (радиус вектора).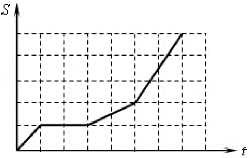

4. Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории.

;

метр/секунду; м/c; d-направление, t-среднее время

Мгновенная скорость направлена по касательной к траектории движения материальной точки.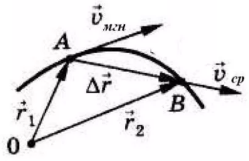

; Модуль мгновенной скорости:

5. Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

; метр на секунду в квадрате, м/с^2

Направление вектора ускорения совпадает с направлением изменения скорости.

6. Мгновенное ускорение — это векторная физическая величина, равная пределу отношения изменения скорости тела к промежутку времени, в течение которого это изменение произошло, при стремлении этого промежутка к нулю.

;

; метр на секунду в квадрате, м/с^2

Направление ускорения также совпадает с направлением изменения скорости Δ

при очень малых значениях промежутка времени, за который происходит изменение скорости.

; Модуль:

7. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело. При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения.

Нормальная составляющая ускорения при криволинейном движении характеризует изменение направления вектора скорости.

;

;метр на секунду в квадрате, м/с^2

Направленна вдоль нормали к траектории движения в данной точке на траектории движения тела. Вектор перпендикулярен линейной скорости движения, направлен по радиусу кривизны траектории.

; an- норм-ая состав-ая ускор-ия, at- танген-ая состав-ая ускор-я, a- полное

8. Тангенциальная составляющая ускорения характеризует быстроту изменения величины скорости за единицу времени. Тангенциальное ускорение всегда коллинеарно скорости. Тангенциальная составляющая характеризует быстроту изменения скорости по модулю

Тангенциальное ускорение — это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

;

; метр на секунду в квадрате, м/с^2

Направление вектора тангенциального ускорения a лежит на одной оси с касательной окружности, которая является траекторией движения тела. Вектор перпендикулярен линейной скорости движения, направлен по радиусу кривизны траектории.

; an- норм-ая состав-ая ускор-ия, at- танген-ая состав-ая ускор-я, a- полное

9.Длина пути:

Геометрическая интерпретация пути: путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.

Формула пути в случае равномерного движения:

10.Длина пути:

11. Первый закон Ньютона гласит, что тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю. Формула:

12. Второй закон Ньютона гласит, что сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение, причем направления силы и ускорения совпадают. Если на тело действует сила, то оно приобретает ускорение.

Формула:

13. Третий закон Ньютона гласит: Взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны. На каждое действие есть своё противодействие. Формула:

14. Принцип относительности Галилея гласит: Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамики одинаковы.

Преобразования Галилея: они устанавливают связь между координатами и временем одной инерциальной системы с координатами и временем другой инерциальной системы, которые движутся друг относительно друга с постоянной скоростью. Равномерное и прямолинейное движение инерциальной системы отсчета не влияет на ход механических процессов, происходящих в этой системе отсчета.

15. 2-ой закон Ньютона в импульсной форме: любое тело, обладающее скоростью, обладает импульсом. Скорость тела будет меняться, когда на него подействует сила и появится ускорение. А если изменяется скорость тела, то будет изменяться его импульс.

Второй закон Ньютона в импульсной форме описывает изменение импульса тела под действием силы. Формула:

; килограмм х метр/сек; кг*м/с

16. Центр масс − точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно (не вращалось).

Формула для радиус-вектора центра масс:

Свойства центра масс системы: 1) всякая система, состоящая из конечного числа материальных точек, имеет центр масс и притом единственный; 2) Центр масс двух материальных точек расположен на отрезке, соединяющем эти точки, его положение определяется архимедовым правилом рычага: произведение массы материальной точки на расстояние от нее; 3) Если в системе, состоящей из конечного числа материальных точек, отметить несколько материальных точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится.

17. Импульс — векторная физическая величина, являющаяся мерой механического движения тела. Формула: ; килограмм х метр/сек; кг·м/с

Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

; v- скорость, p- импульс, m- масса

Закон сохранения импульса — закон, утверждающий, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю. Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы. Формулы: ; ;

18. Работа, формула для общего случая переменной силы: ;

; - для бесконечно малых участков пути.

dA- элементарная работа, F- вектор силы, dr-вектор элементарного перемещения, Fs- проекция силы на касательную к траектории.

Геометрический смысл механической работы заключается в том, что работа силы численно равна площади фигуры под графиком зависимости силы от перемещения тела.

19. Связь между работой и кинетической энергией тела, вывод формулы:

Кинетическая энергия:

;

Элементарная работа по перемещению тела из одной точки в др:

; Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела:

; F- сила, dr- перемещение.

Теорема о кинетической энергии: работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

20. Потенциальная энергия тела вблизи поверхности Земли, формула: E = mgh

Работа силы тяжести при перемещении тела: если тело движется по произвольной траектории, это движение можно представить как «ступенчатое», состоящее из коротких горизонтальных и вертикальных участков. Суммарная работа силы тяжести на всех горизонтальных участках равна нулю, а алгебраическая сумма работ на всех вертикальных участках равна

где

— начальная высота тела,

— его конечная высота.

21.Консервативные силы — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки.

Чему равна работа консервативной силы по любому замкнутому пути, почему: работа консервативных сил при перемещении частицы по замкнутой траектории равна нулю.

; для замкнутой траектории начальная точка совпадает с конечной, поэтому никакой работы не может быть.

22. Диссипативные силы — это силы, у которых работа является зависимой от перемещения тела, точнее от траектории этого движения. При этом механическая энергия этого тела переходит в немеханическую. Диссипативные силы - это не потенциальные силы.

Чему равна работа диссипативной силы по любому замкнутому пути, почему: работа диссипативной силы по замкнутой траектории нулю не равна. Например, работа силы трения всегда отрицательна, ибо сила направлена против перемещения. Работа диссипативной силы всегда отрицательна.

23. Связь между силой и потенциальной энергией, вывод формулы: пространство, в котором действуют консервативные силы, называется потенциальным полем, каждой точке этого поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии Eп.

24. Закон сохранения механической энергии: сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Это утверждение выражает закон сохранения энергии в механических процессах. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии. Формула:

25. Закон изменения механической энергии: изменение полной механической энергии системы тел происходит при совершении работы силами, действующими как между телами системы, так и со стороны внешних тел. Изменение механической энергии ∆E системы тел определяется законом изменения полной механической энергии.

Формула: ∆E = E2 − E1 = Aвнеш + Aтр(сопр); E1 — полная механическая энергия начального состояния системы; E2 — полная механическая энергия конечного состояния системы; Aвнеш — работа, совершаемая над телами системы внешними силами; Aтр(сопр) — работа, совершаемая силами трения (сопротивления), действующими внутри системы.

26. Угловое перемещение — это видимое перемещение объекта в полярной системе координат, точкой отсчета которой является наблюдатель перпендикулярно лучу его зрения. Угловое перемещение (угол поворота) — это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2. Формула: ;

ω - угловая скорость, φ- угловое перемещение, е- угловое ускорение; измеряется в рад.

Направление углового перемещения совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.

27.Угловая скорость— векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно центра вращения. Угловая скорость (обозначается как ω) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.

Формула: ω=△φ/△t;

;(φ) - угол поворота, (t)- интервал времени; радиан в секунду (рад/с)

Направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.

28. Угловое ускорение ε – физическая величина, характеризующая изменение угловой скорости при движении тела. Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела.

Формула: ;

Направление углового ускорения совпадает с вектором угловой скорости при равноускоренном движении и противоположно при равнозамедленном.

29. Связь угловой и линейной скорости: можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет: 2πR. Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:

; зная, что:

; получим справедливое равенство:

; Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

30. Связь углового ускорения и компонент линейного ускорения: с изменением угловой скорости точки меняется и ее линейная скорость. Нормальное ускорение связано с угловой скоростью и не зависит, следовательно, от углового ускорения. Но тангенциальное ускорение выражается через угловое ускорение:

Связь полного линейного ускорения с угловым ускорением:

31.Момент инерции материальной точки и АТТ относительно оси вращения: называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения. (!) Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения. Формула: ;

Теорема Штейнера: момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения. Формула: ; J- искомый момент инерции относительно параллельной оси, Jc- известный момент инерции относительно оси, проходящей через центр масс тела, d- расстояние между указанными осями.

32. Момент силы относительно оси вращения — это величина, характеризующая действие силы на тело, которое может поворачиваться вокруг заданной оси. Моментом силы (

)

относительно оси называется векторное произведение радиуса вектора

, проведённого из т. 0 в точку приложения силы

, и силы

Формула: ; Н^.м; Направление вектора

определяется по правилу произведения векторов или по правилу правого винта.

33. II закон Ньютона для вращательного движения АТТ, определение: скорость изменения момента импульса L тела, вращающегося вокруг неподвижной точки, равна результирующему моменту всех внешних сил M, приложенных к телу, относительно этой точки. Формулы: dL/dt = M;

; a- вектор ускорения.

34. Момент импульса материальной точки и АТТ, формула: mVr = L;

; r- радиус-вектор, p- импульс материальной точки, L- момент импульса; м^2·кг/с

Направление совпадает с направлением поступательного движения правого винта при его вращении от

Связь момента импульса и момента инерции: Связь прямо пропорциональная. Момент импульса ведь равен моменту инерции, умноженному на угловую скорость вращения.

35. II закон Ньютона для вращательного движения АТТ через момент импульса: импульс действующей силы равен изменению импульса объекта. Угловое ускорение при вращательного движении АТТ вокруг закреплённой оси прямо пропорционально алгебраической сумме моментов всех внешних сил, действующих на него, и обратно пропорционально моменту инерции АТТ. Формулы: М = dL/dt; L=Iw; E=M/I; M=IE; I- момент инерции, w- угловая скорость,

36. Закон сохранения момента импульса, определение: если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.
Формулы: , то

, откуда

; L- момент импульса, M-момент внешних сил.

37. Кинетическая энергия вращающегося тела, формула: ; ; I-момент инерции (тела), ω - угловая скорость.

При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:

Работа внешних сил при вращении твердого тела, формула: ;

M-момент внешних сил, φ - угол поворота.
38-39. Момент инерции бесконечно тонкого кольца, вывод формулы: для вычисления момента инерции воспользуемся формулой:

, где расстояния от любого элемента кольца равно его радиусу, то есть:

, в таком случае момент инерции тонкого кольца равен:

40. Момент инерции диска или сплошного цилиндра, вывод формулы: , где

, тогда момент инерции цилиндра относительно его собственной оси равен:

41. Момент инерции однородного шара, вывод формулы: по условию шар является однородным, плотность его можно представить как:

, где

,

в качестве элементарной массы выберем сферический слой радиуса r Его массу можно представить как:

, при этом объем рассматриваемого сферического слоя равен:

, момент инерции тонкого диска равен:

, выделенный нами диск находится на расстоянии h от центра шара. Радиус рассматриваемого нами диска связан с расстоянием h выражением:

, тогда формулу

преобразуем к виду:

, просуммируем моменты инерции всех дисков:

42.Момент инерции однородного стержня относительно оси, проходящей через его центр инерции, вывод формулы: общая формула: I = ∫_V(ρ*r²*dV), Обозначим площадь сечения стержня буквой S, теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем: I = ∫_L(ρ*S*l²*dl), остается только подставить правильные пределы интегрирования и записать конечную формулу: I = ∫_-L/2^L/2(ρ*S*l²*dl)=

I = M*L²/12

Момент инерции однородного стержня относительно оси, проходящей через его край, вывод формулы: выделим элемент dr с массой dm, находящийся на расстоянии r от оси вращения, момент инерции выделенного элемента: dJ = r²dm = r²ρSdr, где ρ – плотность стержня, S – площадь поперечного сечения, момент инерции всего стержня относительно оси:

43. Постулаты Эйнштейна: 1) во всех инерциальных системах отсчета все физические явления (механические и электромагнитные) протекают одинаково. 2) скорость света в вакууме является предельной скоростью любого взаимодействия и не зависит от скорости движения источника. Преобразования Лоренца: Лоренц установил связь между координатами и временем события в системах отсчета k и k' основываясь на тех экспериментальных фактах, что: все инерциальные системы отсчета физически эквивалентны; скорость света в вакууме постоянна и конечна, во всех инерциальных системах отсчета и не зависит от скорости движения источника и наблюдателя.

Эффект сокращения длины- предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя, движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета. Эффект замедления времени- физический эффект специальной теории относительности, заключающийся в том, что с точки зрения наблюдателя, все физические процессы в движущейся относительно него системе отсчёта проходят медленнее. Закон сложения скоростей в специальной теории относительности- ;

Элементы динамики СТО: импульс, релятивистская масса и масса покоя, энергия, связь импульса и энергии в СТО: импульс: р = vE/c²; p = mu (u-скорость); масса:

, E- полная энергия свободного тела, р- импульс, с- скорость света; масса покоя: масса объекта, находящегося в состоянии покоя, масса покоя электрона приблизительно равна 9,11×10⁻³¹; энергия: Е² – р² с²= m²c⁴; связь импульса и энергии в СТО: