22-04-2020-Лекция_размерные_цепи_Сырицкий. Размерные цепи
 Скачать 4.57 Mb. Скачать 4.57 Mb.
|
|
РАЗМЕРНЫЕ ЦЕПИ Размерная цепь – это совокупность взаимосвязанных размеров, образующих замкнутый контур и определяющих точность взаимного расположения осей и поверхностей одной детали (подетальная размерная цепь) или нескольких деталей в узле или механизме (сборочная размерная цепь). 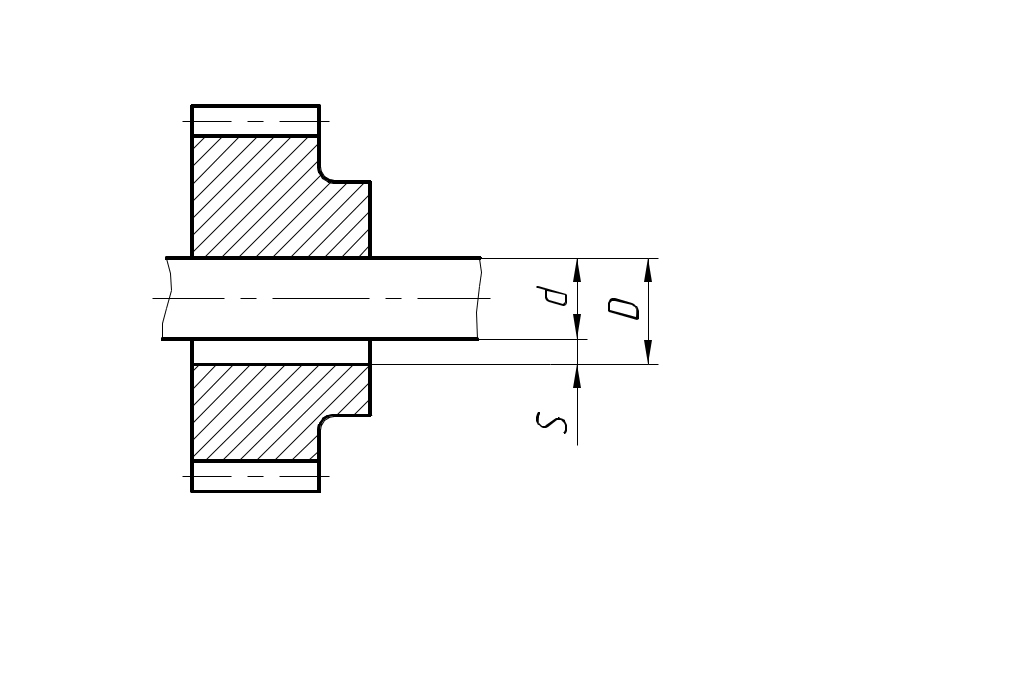 Рис.1 Сборочная размерная цепь 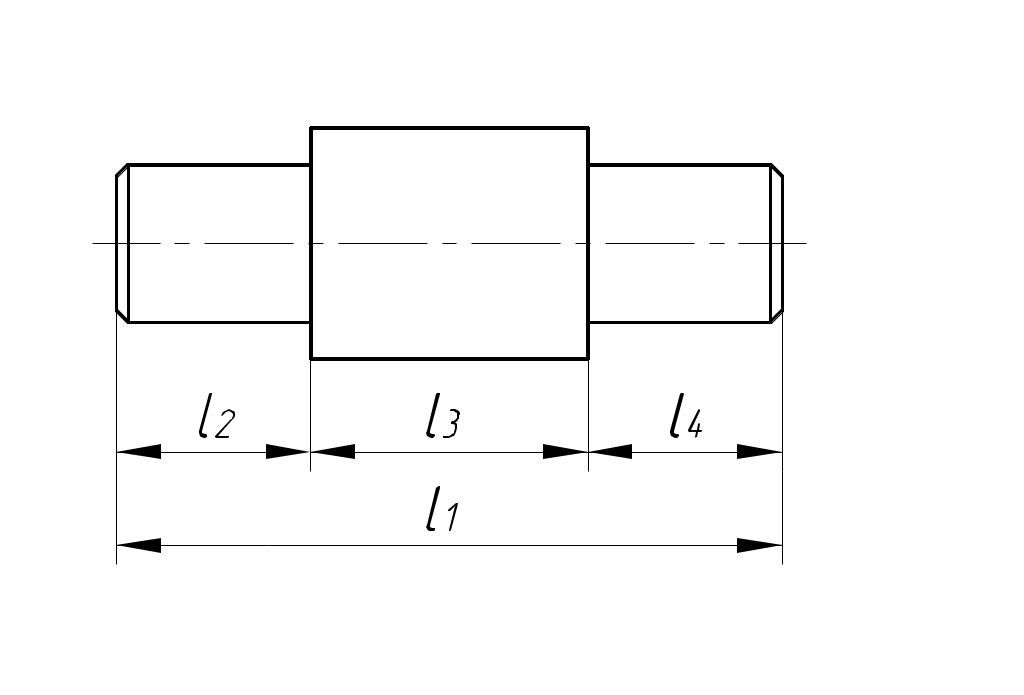 Рис.2 Подетальная размерная цепь По взаимному расположению звеньев размерные цепи делятся на: линейные 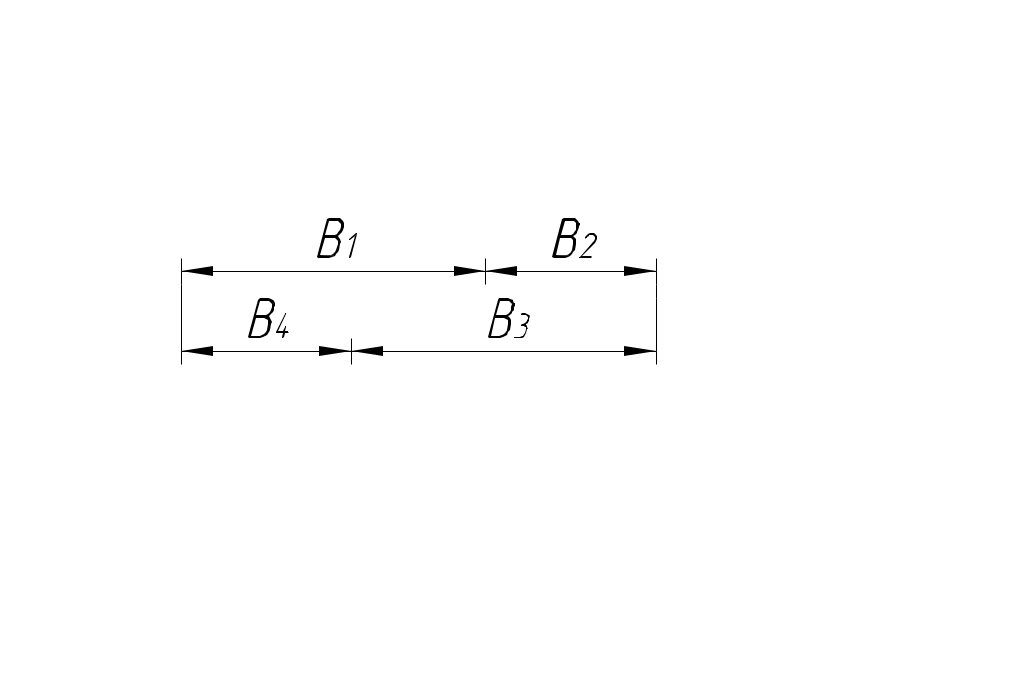 плоские 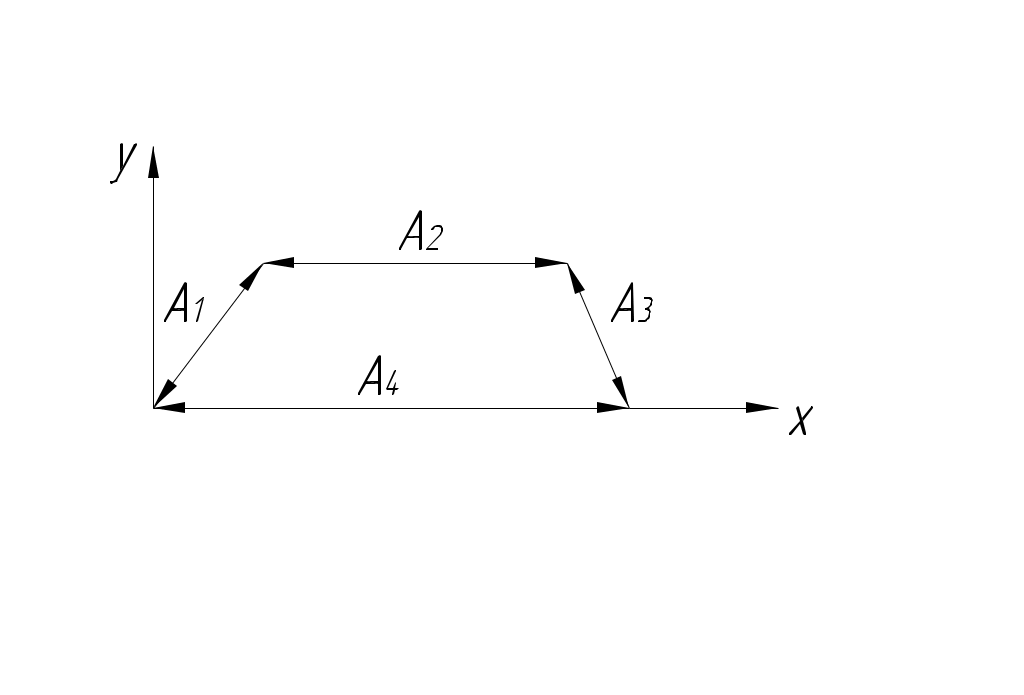 пространственные 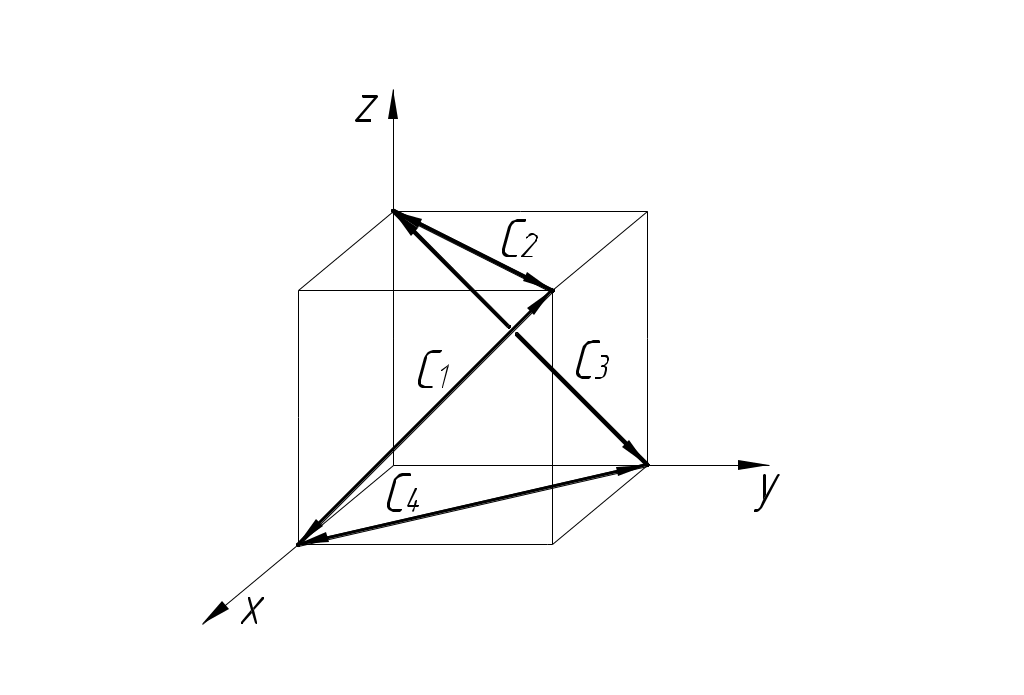 Все звенья размерных цепей делятся на составляющие и одно замыкающее. Замыкающий размер – это размер, который получается последним в ходе обработки детали или сборки узла. Это необрабатываемый размер, его величина и точность зависят от величины и точности остальных размеров цепи, называемых составляющими. Пример 1. Последовательность обработки: 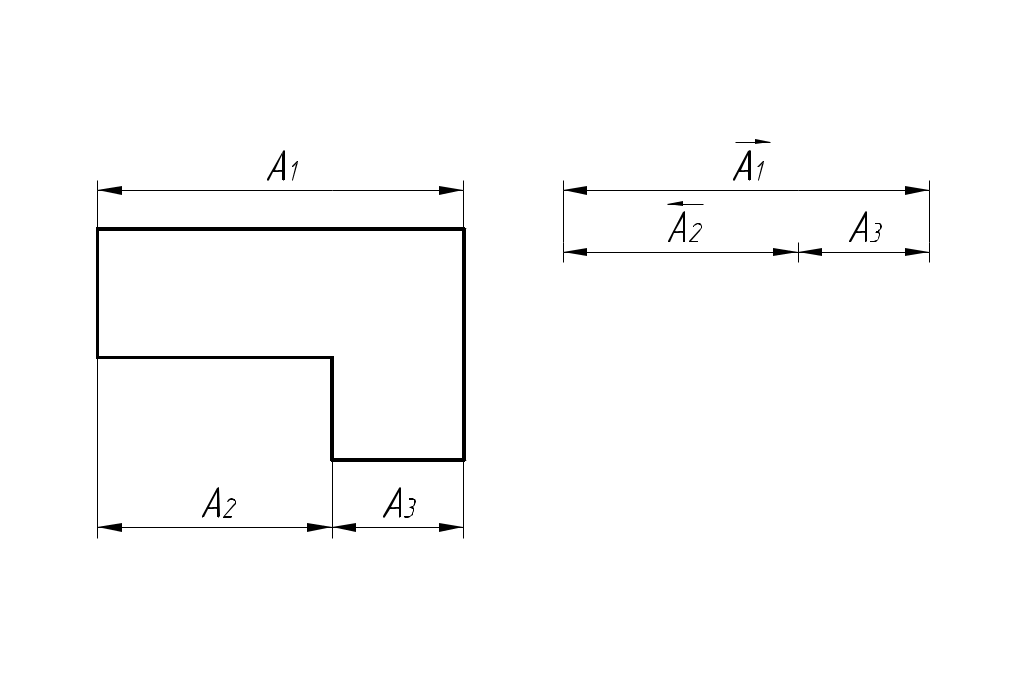 Замыкающий размер: Составляющие размеры: В зависимости от влияния на замыкающий размер Увеличивающий размер – это составляющий размер, с увеличением которого замыкающий размер увеличивается. Уменьшающий размер – это составляющий размер, с увеличением которого замыкающий размер уменьшается. Пример 2. 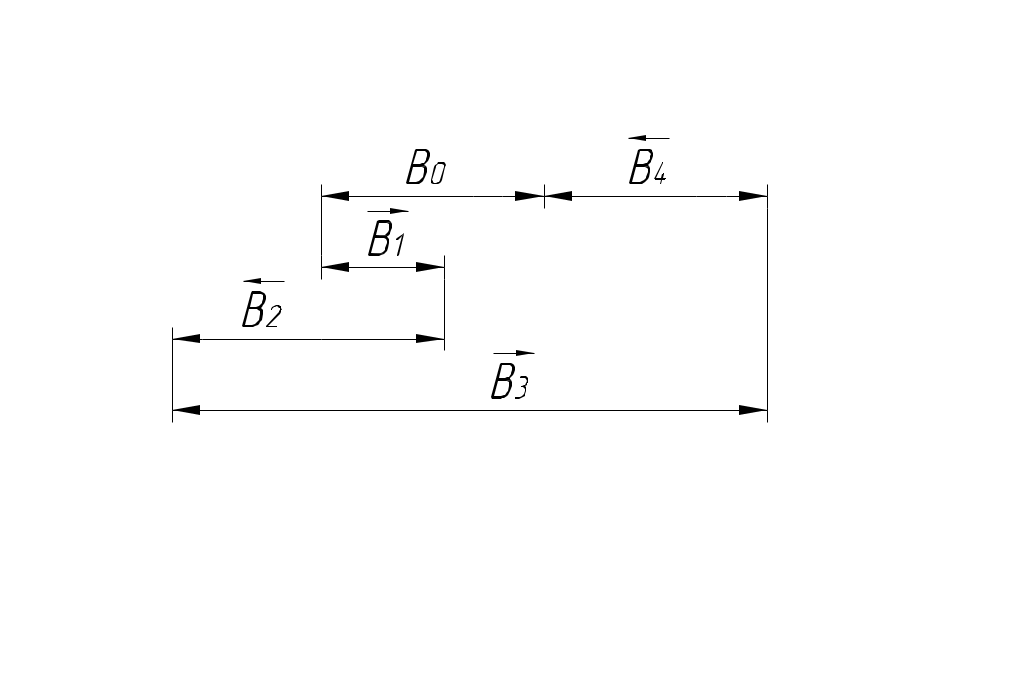 Увеличивающие размеры: Уменьшающие размеры: Среди всех звеньев цепи выделяют исходный размер. Исходный размер – это размер, определяющий функционирование механизма (зазор, натяг и т.п.). Исходя из его точности, определяют точность остальных размеров цепи. При решении размерных цепей встречаются два типа задач: задача анализа или проверочный расчет: необходимо определить номинальный размер и предельные отклонения замыкающего звена по заданным номинальному размеру и предельным отклонениям составляющих звеньев. задача синтеза или проектный расчет: необходимо назначить допуски и предельные отклонения на составляющие размеры по заданным допуску и предельным отклонениям замыкающего звена и номинальным размерам всех звеньев цепи. При решении размерных цепей используют следующие методы: метод полной взаимозаменяемости (метод максимума-минимума); вероятностный метод; метод регулирования; метод групповой взаимозаменяемости (селективная сборка); метод пригонки. Расчет размерных цепей методом полной взаимозаменяемости Этот метод позволяет производить сборку без дополнительной обработки, пригонки, регулирования. Используется в размерных цепях с небольшим числом составляющих размеров. 1. задача анализа 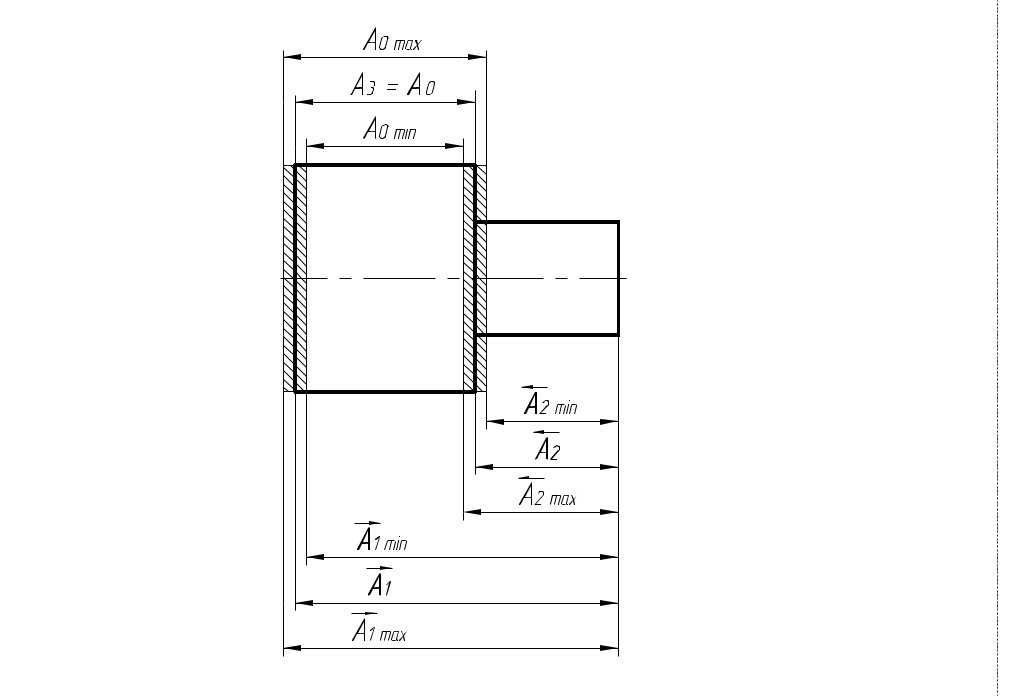 Последовательность обработки: Номинальный размер замыкающего звена: В общем случае номинальный размер замыкающего звена: где n – это число увеличивающих звеньев; p – число составляющих звеньев. Предельные размеры замыкающего звена: В общем случае предельные размеры замыкающего звена: Из формул (2) и (3) получаем: 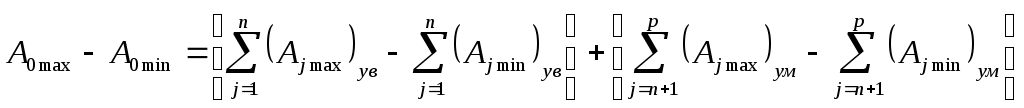 , ,где m – это общее число звеньев: m − 1 = p. Формула (4) выражает сущность расчета размерных цепей методом максимума-минимума: допуск замыкающего звена равен сумме допусков составляющих звеньев. Из формулы (4) следуют два вывода: размер, к которому предъявляют наиболее высокие точностные требования, т.е. исходный размер, по возможности должен быть составляющим, а не замыкающим; размерная цепь должна быть наикратчайшей, т.е. содержать наименьшее число звеньев. Введем обозначение: где Подставляя выражения (5) и (6) в формулы (2) и (3), получим: Решение задачи анализа производится по формулам (1), (7), (8) с проверкой по формуле (4). 2. задача синтеза Эта задача решается двумя способами: а) способ равных допусков Если номинальные размеры всех составляющих звеньев попадают в один интервал размеров, то можно принимать, что б) способ равноточных допусков Предполагают, что все составляющие размеры обрабатываются по одному и тому же квалитету, а допуск в каждом квалитете подсчитывается по формуле: где Так как все составляющие размеры обрабатываются по одному квалитету, то где 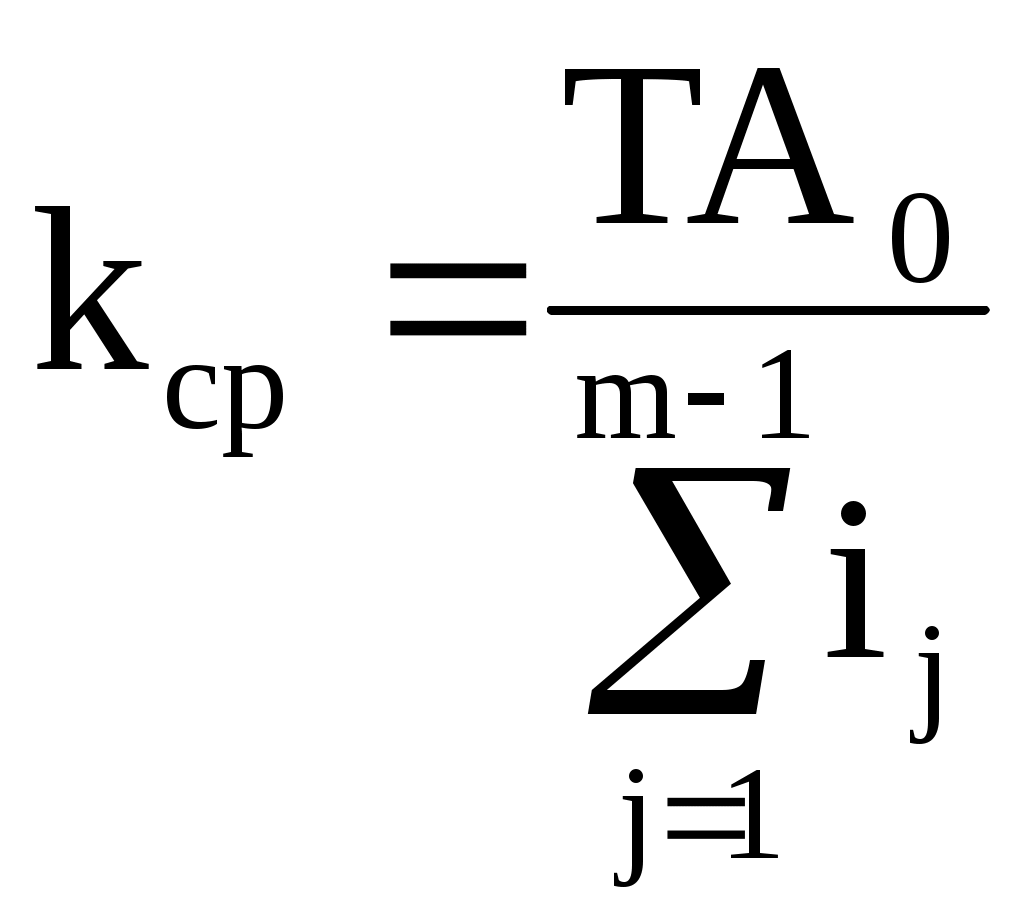 . (10) . (10)По значению среднего коэффициента точности размерной цепи Вероятностный метод расчета размерных цепей 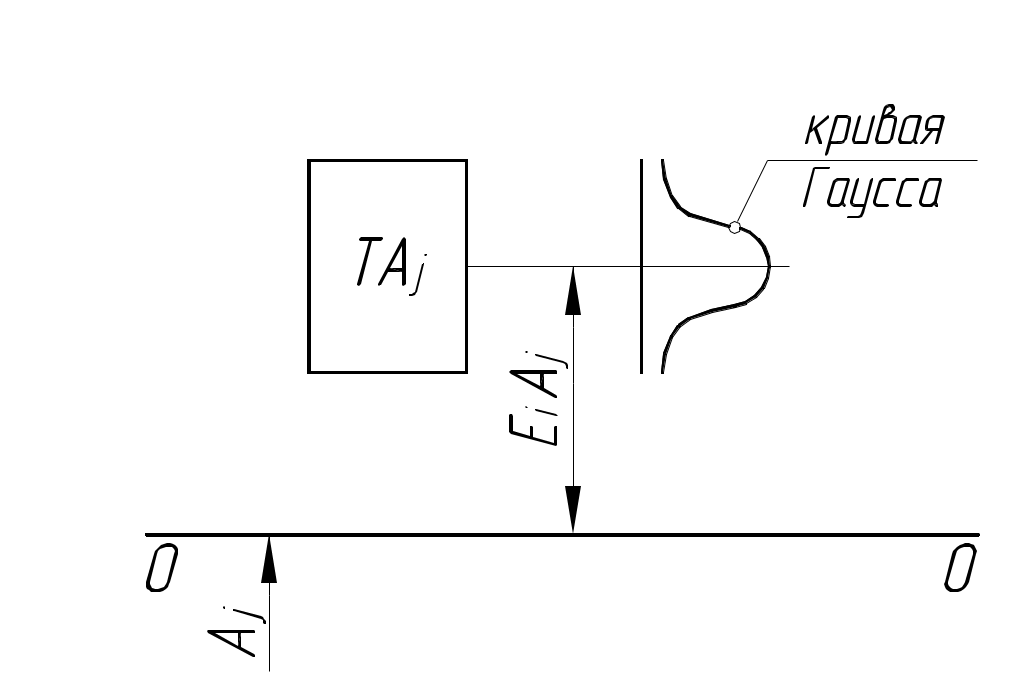 С доверительной вероятностью P = 0,9973 где Формула (11) выражает сущность расчета размерной цепи вероятностным методом: допуски складываются квадратически. Следует помнить, что у 0,027% деталей размеры могут оказаться за пределами поля допуска. Если такой риск допустим, то можно использовать вероятностный метод; если недопустим (связан с опасностью для жизни людей) – то метод максимума-минимума. задача анализа (проверочный расчет) Определяют допуск по формуле (11): Определяют координаты середины поля допуска звена Формулы (7) и (8) не выполняются. 2. задача синтеза а) способ равных допусков б) способ равноточных допусков 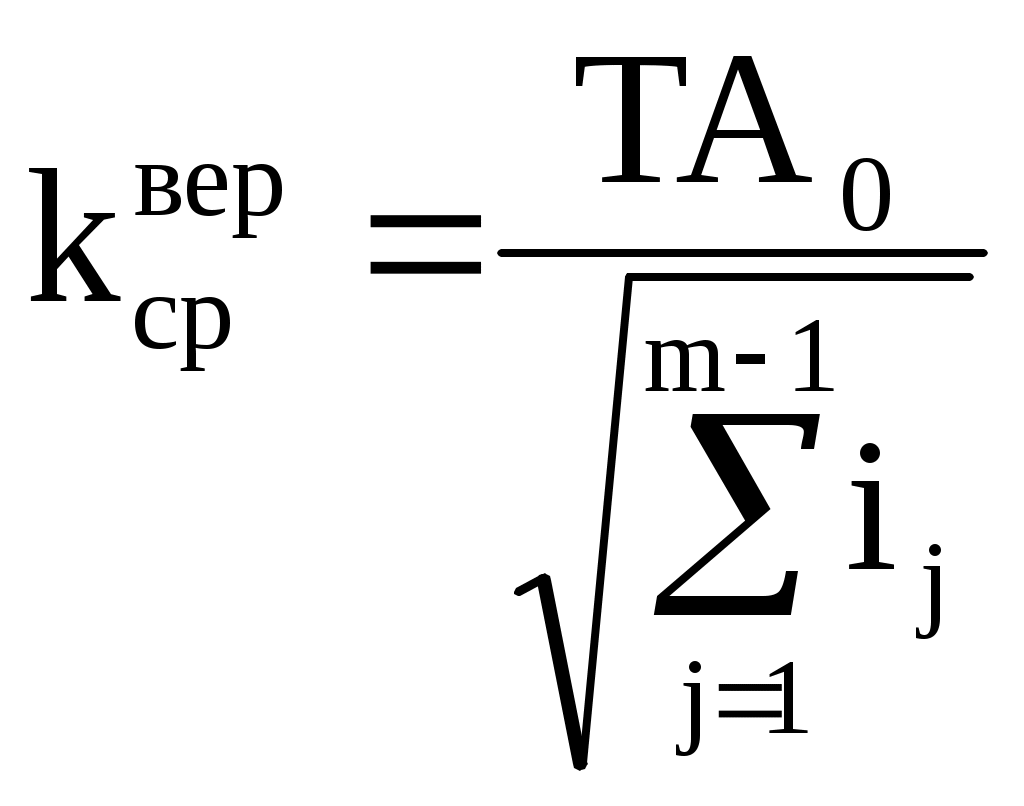 . (16) . (16)Вероятностный метод по сравнению с методом максимума-минимума позволяет: при решении задачи анализа получить более узкий, но более вероятный допуск замыкающего звена. при решении задачи синтеза при том же допуске замыкающего звена назначить более широкие допуски составляющих звеньев. Пример 1.  Последовательность обработки: Определить x. Решение. 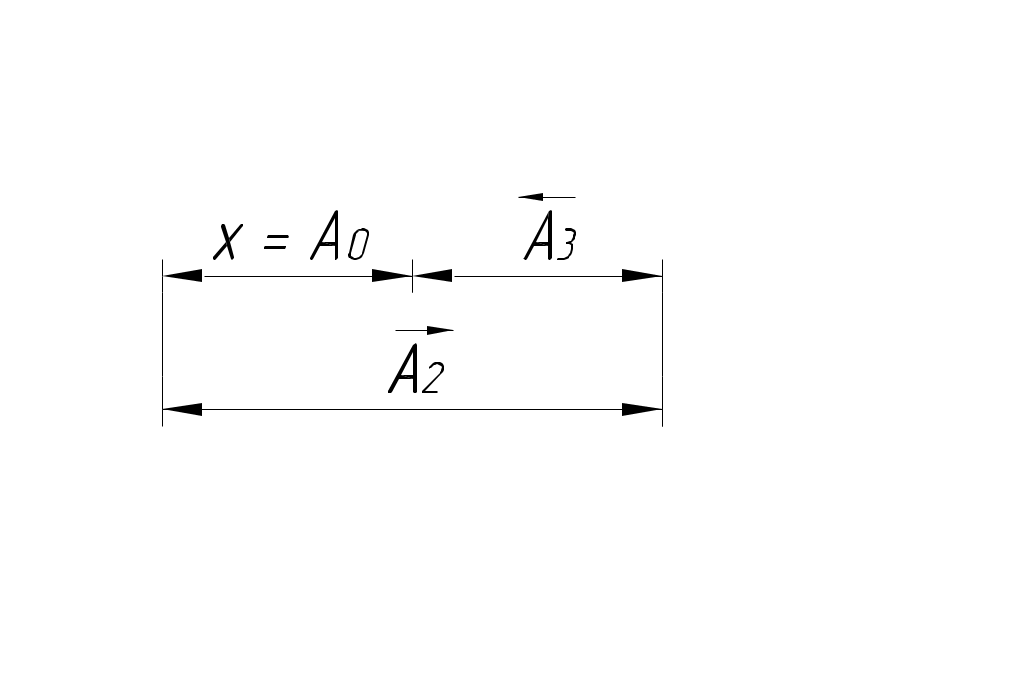 метод максимума-минимума Проверка: вероятностный метод 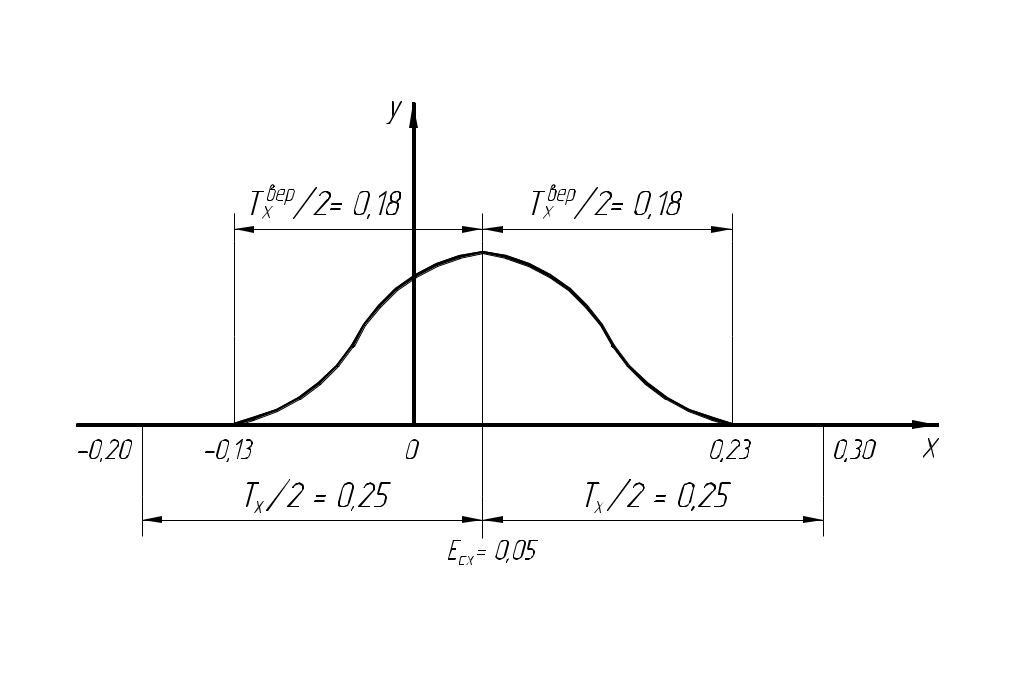 Вероятностный метод позволяет получить более узкий допуск замыкающего звена по сравнению с методом максимума-минимума. Пример 2. 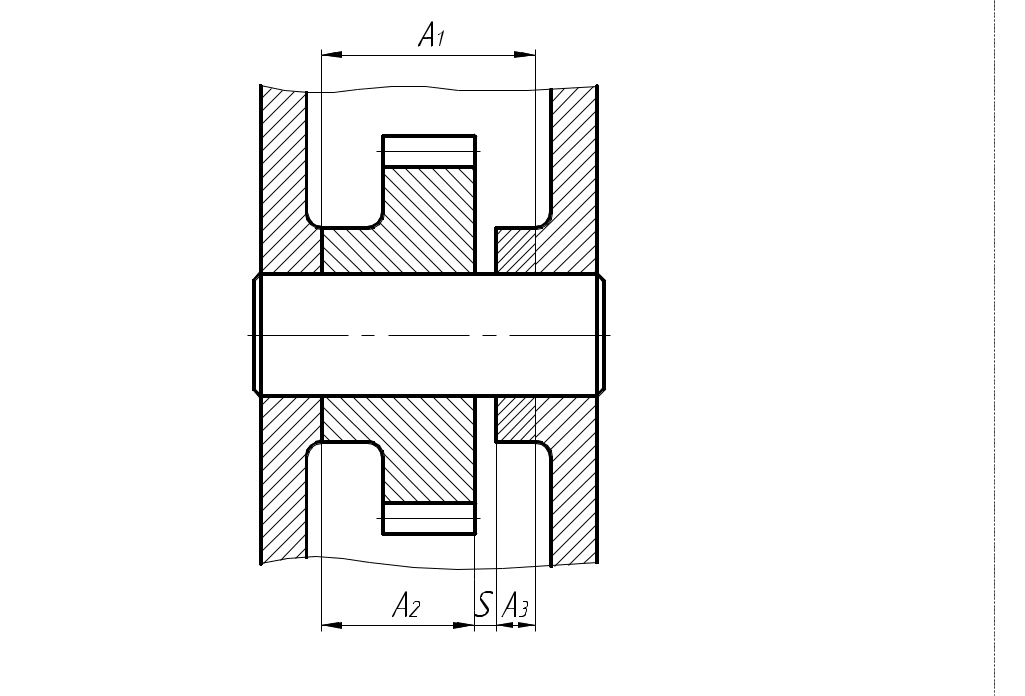 Решение. 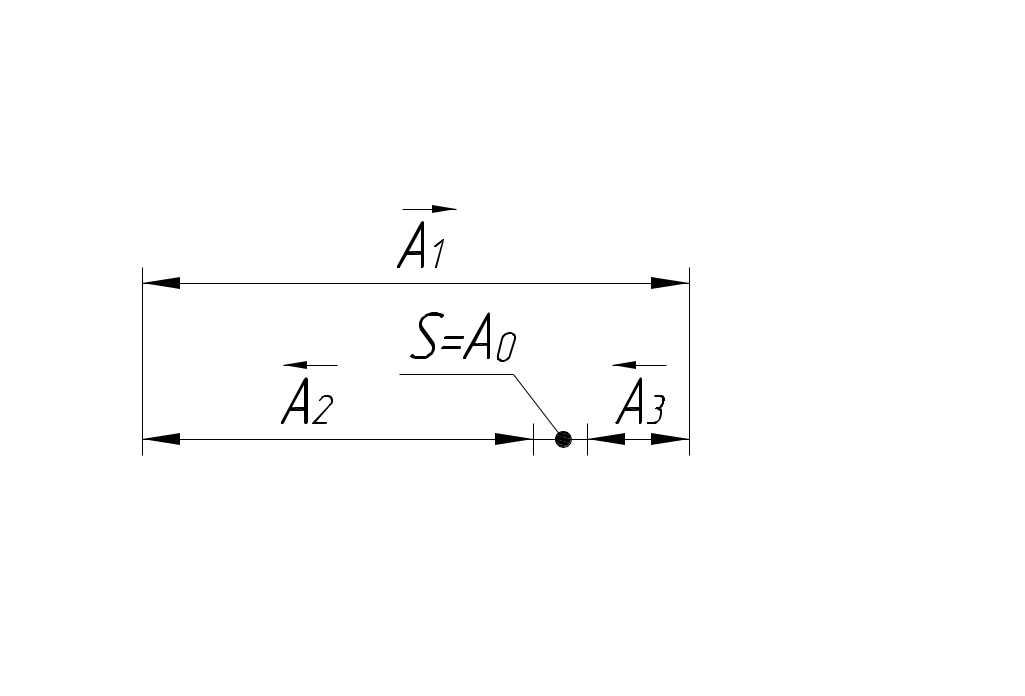 Это задача синтеза (проектный расчет). Решаем ее способом равноточных допусков.
Расчет размерных цепей методом регулирования При методе регулирования составляющие размеры обрабатывают с расширенными технологически легко выполнимыми точностями, а заданная точность замыкающего звена получают изменением размеров (регулированием) одного из заранее выбранных звеньев, называемого компенсатором. В качестве компенсаторов используют наборы прокладок, клинья и т.п. 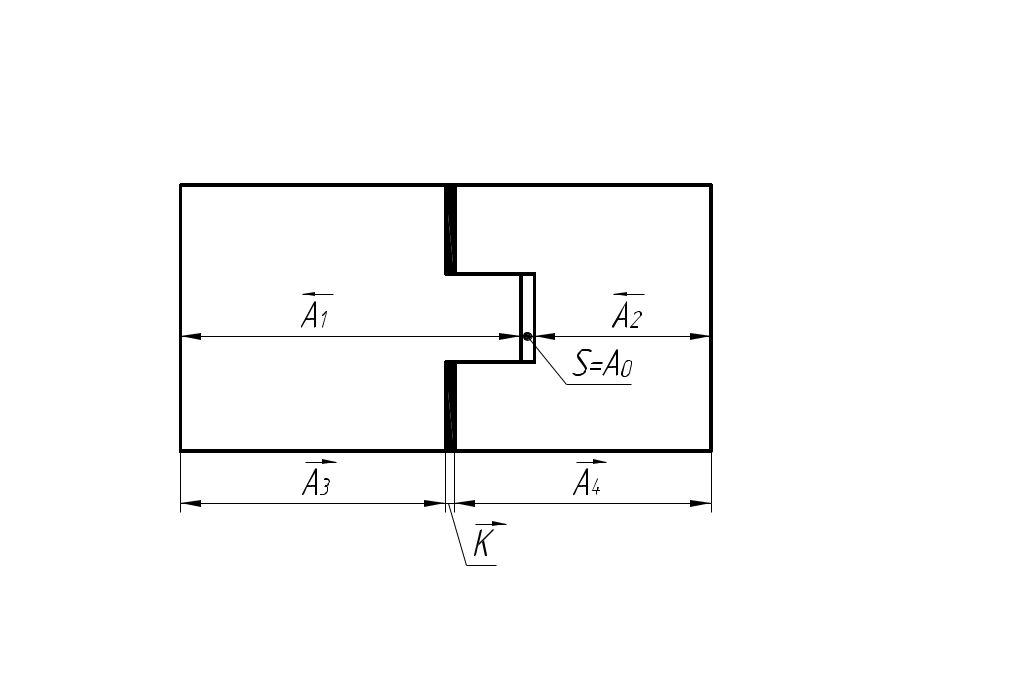 Номинальный размер компенсатора K где "+" − при K – увеличивающее звено; "-" − при K – уменьшающее звено. Предельные отклонения компенсатора: а) K – увеличивающее звено б) K – уменьшающее звено Вычитая (3) из (2) или (5) из (4), получим: где Из формулы (6) следует, что метод регулирования используется в том случае, если Расчет числа и толщины прокладок компенсатора Компенсатор выпускаются в виде набора прокладок двух типов: одна постоянная прокладка несколько прокладок разной толщины. Толщина сменной прокладки: Поэтому число прокладок округляем до целого числа в меньшую сторону. округляем в меньшую сторону до стандартного значения из ряда Ra10. Проверка: Преимущества метода регулирования: при решении задачи анализа позволяет получить более узкий допуск замыкающего звена при тех же допусках составляющих звеньев (по сравнению с методом максимума-минимума); при решении задачи синтеза позволяет при том же допуске замыкающего звена назначить более широкие допуски составляющих звеньев. Недостатки: усложняется конструкция узла из-за использования дополнительных деталей; увеличивается трудоемкость сборки. Пример выполнения ДЗ номер 2. См. эскиз I. Обработка размеров Величина размера Решение. схема размерной цепи 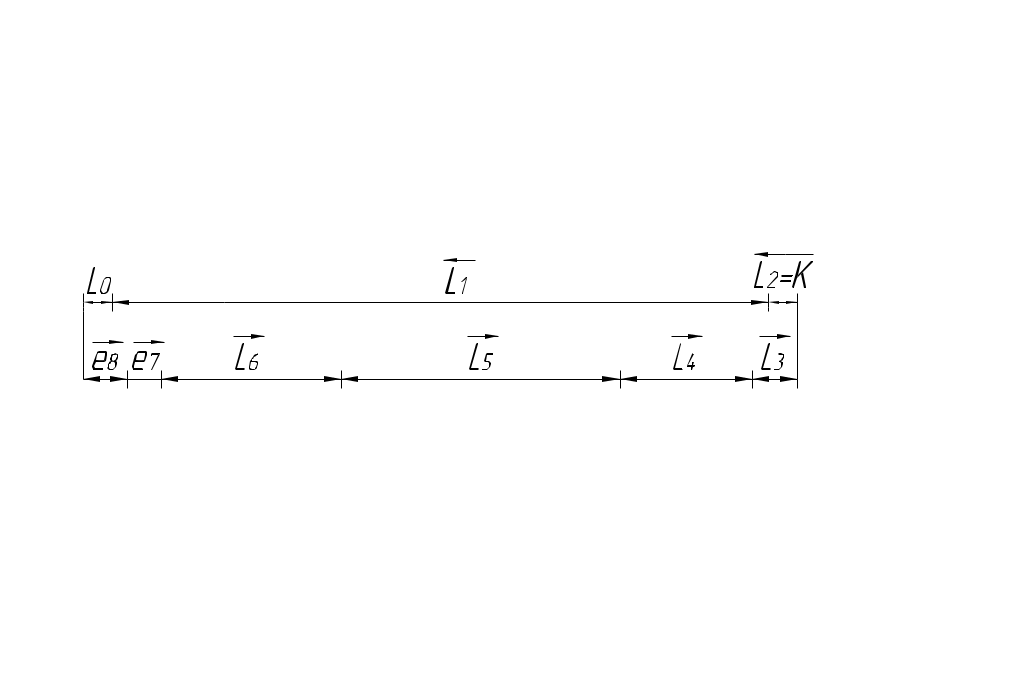 назначаем предельные отклонения на составляющие размеры (в тело металла): 4. находим предельные отклонения компенсатора Проверка: определяем число и толщину прокладок компенсатора Проверка: Увеличиваем число прокладок: N = 7. Пример 2. Назначить допуски и предельные отклонения для двух вариантов обработки вала: а) б) Решение. а) 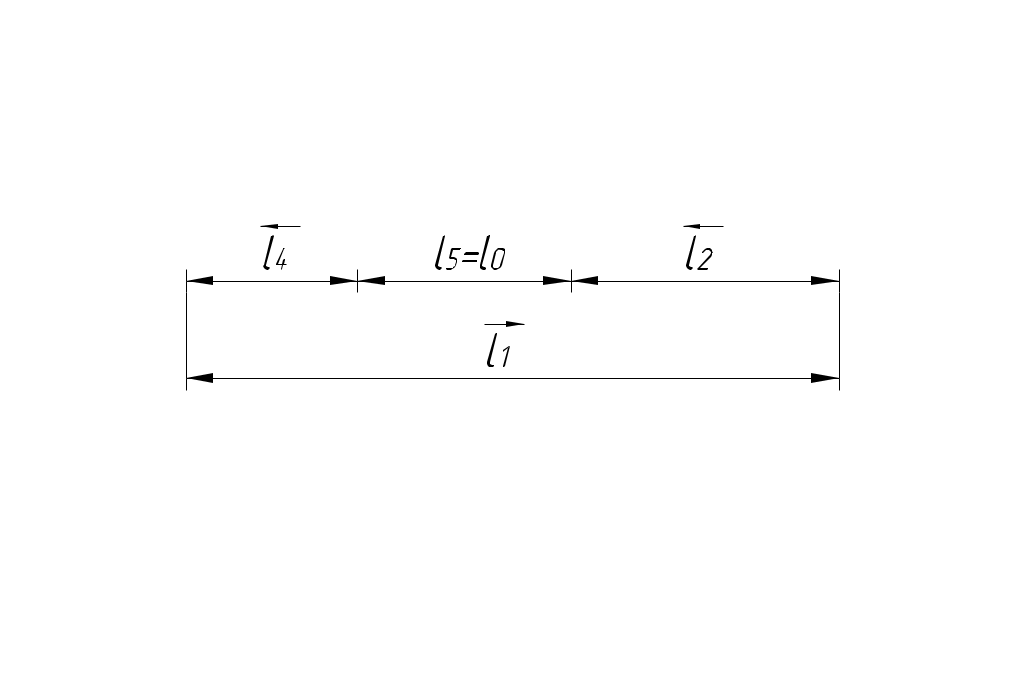 Исходный размер: Это задача синтеза. Решаем ее способ равноточных допусков. 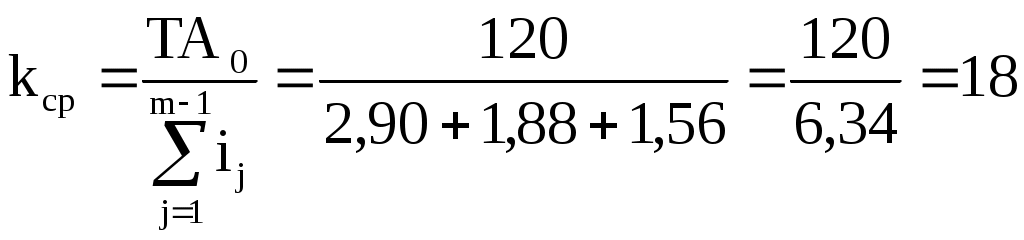 (по таблице 2), (по таблице 2),IT7 IT8
Назначаем предельные отклонения на все размеры кроме звена увязки (в тело металла): б) 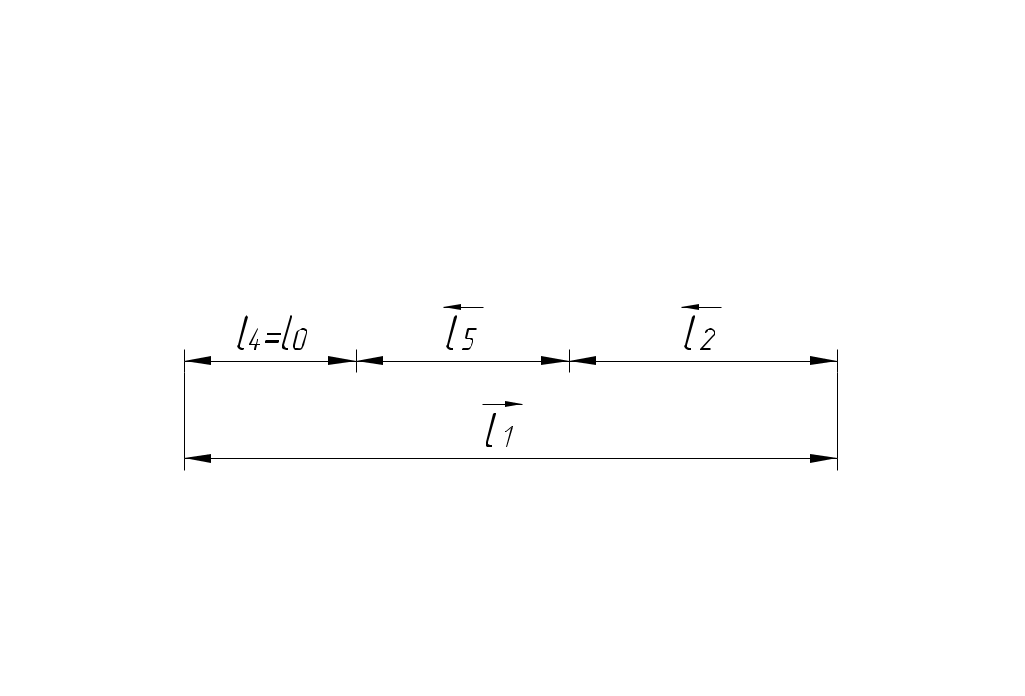 Исходный размер Определим замыкающий размер: Вывод: вариант обработки б) экономически более выгодный, т.к. размеры обрабатываются с большими допусками (IT10 вместо IT7). 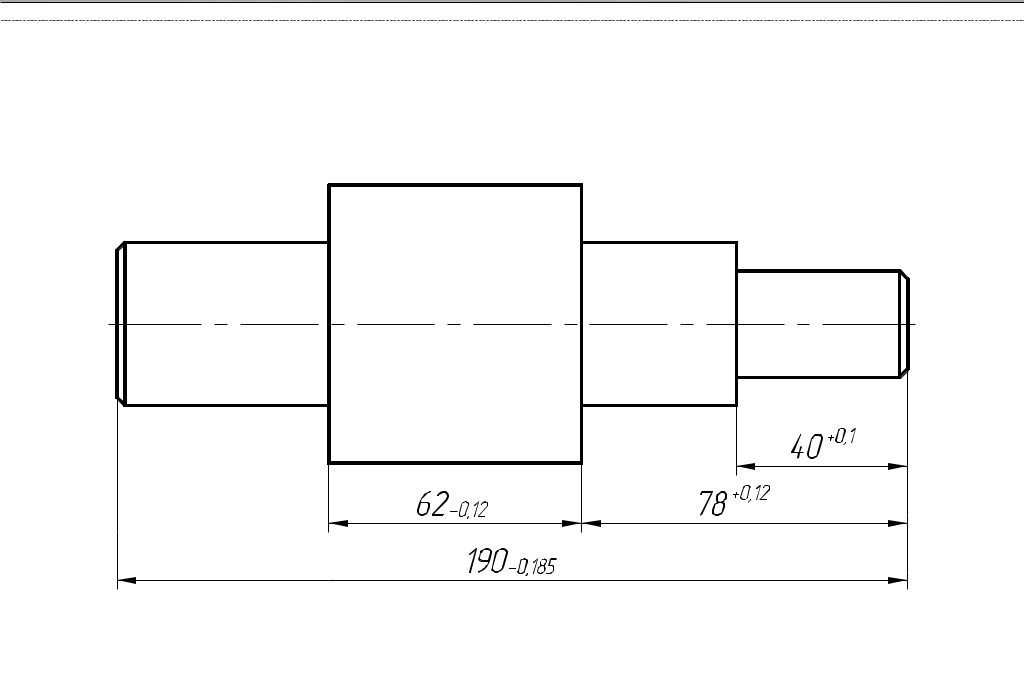 Примеры решения задач Пример 1. 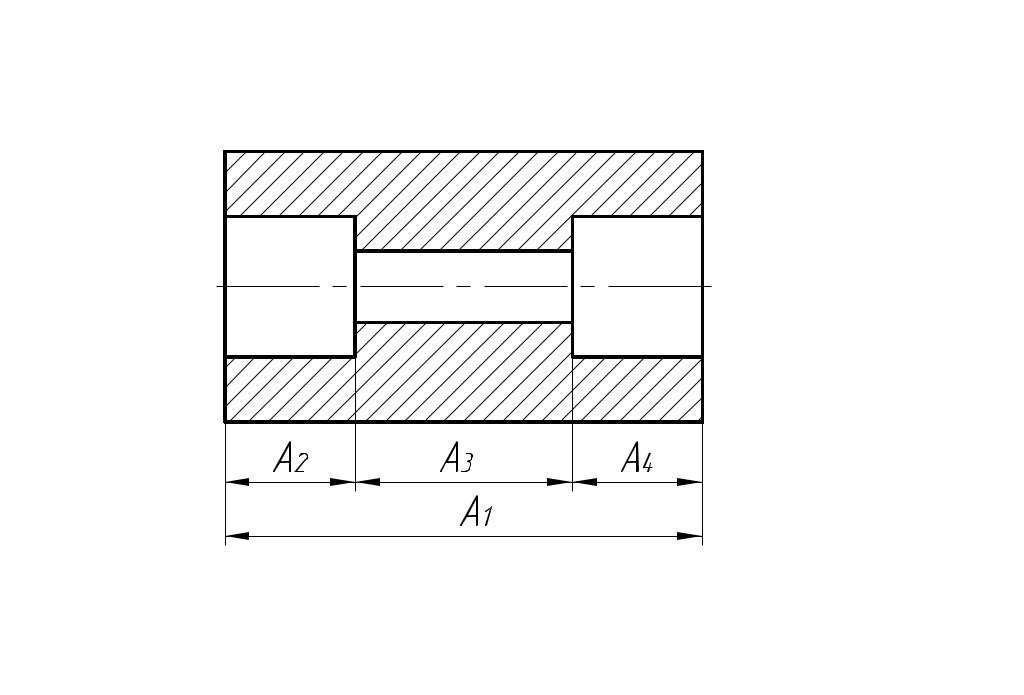 Последовательность обработки: Определить Решение. 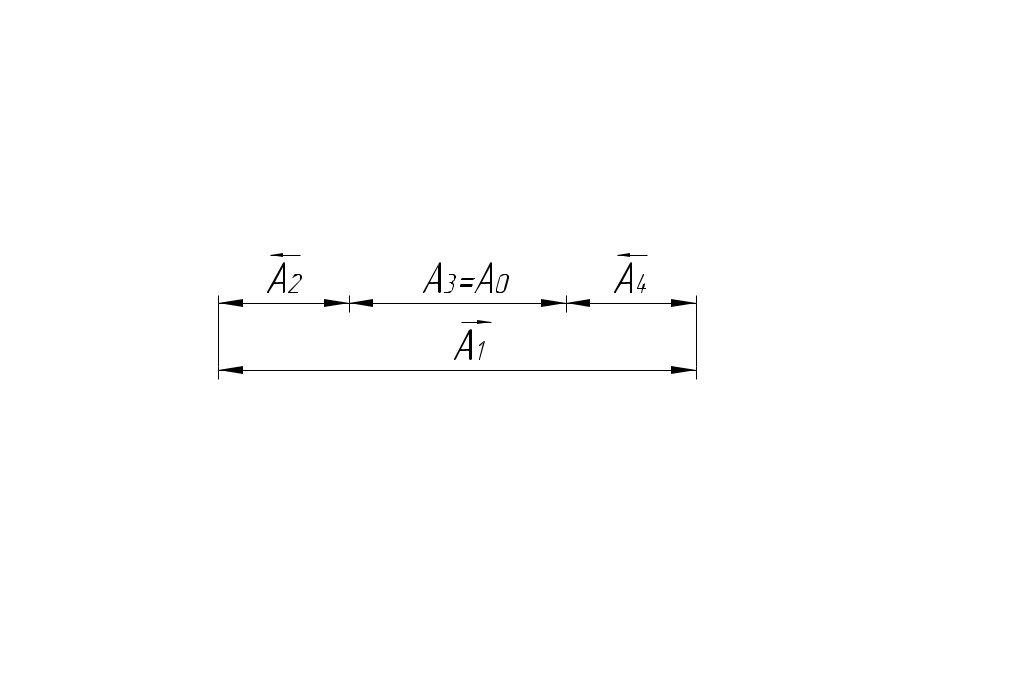 Ответ: Пример 2. 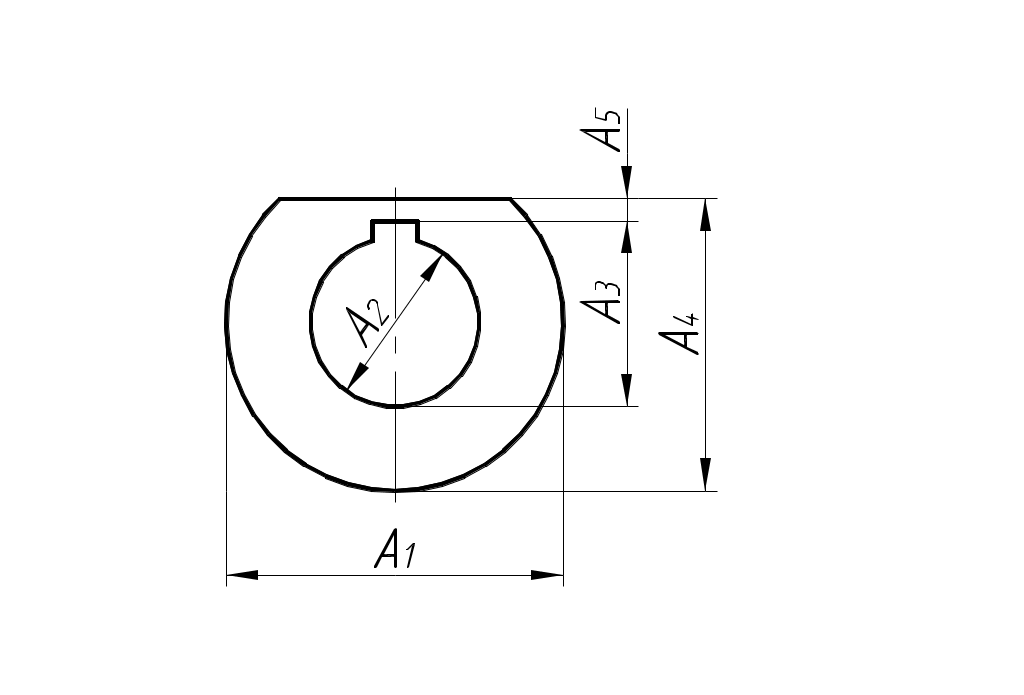 Последовательность обработки: А1 = Ø А2 = Ø Определить Решение. 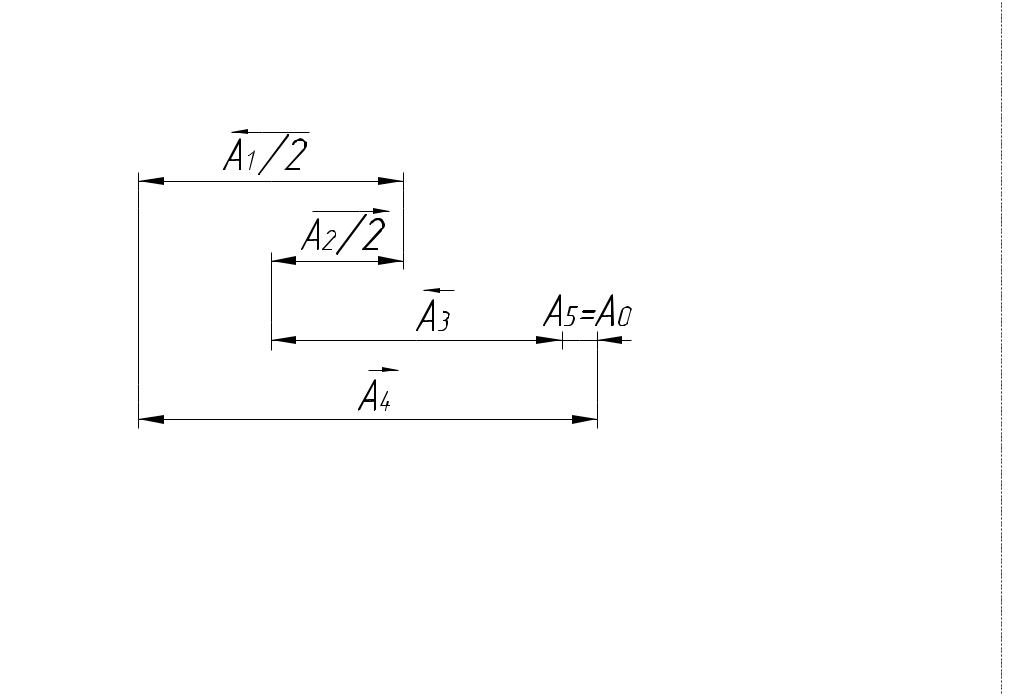 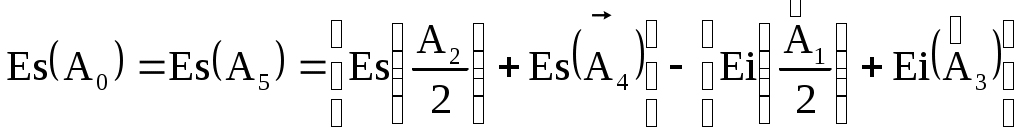 , ,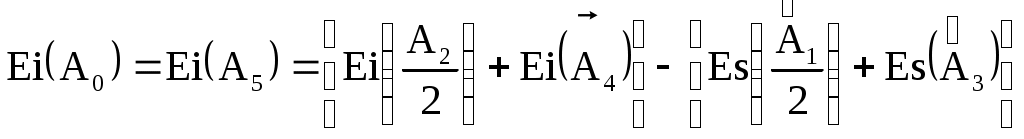 , ,Ответ: |
