Курсовая работа на печать2. Разработка цифрового фильтра нижних частот (фнч) на основе применения треугольной оконной функции Бартлетта
 Скачать 299.63 Kb. Скачать 299.63 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тамбовский государственный университет имени Г.Р.Державина» Курсовая работа По цифровой обработке сигналов на тему: «Разработка цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта» Выполнил: студент 3 курса группа 01/3023 Агапов А.А. Научный руководитель: Кандидат технических наук, доцент, доцент кафедры теоретической и экспериментальной физики Суслин М.А. Тамбов 2022 СОДЕРЖАНИЕ ВВЕДЕНИЕ 4 1 Цифровая обработка сигналов 5 2 Цифровой фильтр 6 2.1 Общие сведения и применение 6 2.2 Характеристика цифровых фильтров 6 2.3 Достоинства и недостатки 7 2.4 Виды цифровых фильтров 8 3 Фильтр нижних частот 9 3.1 Общие сведения 9 3.2 Применение 9 4 Оконные функции 11 5 Ход работы 12 5.1 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=10 12 5.1.1 Исходные данные 12 5.1.2 Прямоугольное окно 12 5.1.3 АЧХ прямоугольного окна 14 5.1.4 АЧХ фильтра 15 5.2 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=20 16 5.2.1 Исходные данные 16 5.2.2 Прямоугольное окно 16 5.2.3 АЧХ прямоугольного окна 18 5.2.4 АЧХ фильтра 19 5.3 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=100 20 5.3.1 Исходные данные 20 5.3.2 Прямоугольное окно 20 5.3.3 АЧХ прямоугольного окна 22 5.3.4 АЧХ фильтра 23 ЗАКЛЮЧЕНИЕ 24 СПИСОК ЛИТЕРАТУРЫ 25 ВВЕДЕНИЕ Цифровая обработка сигналов представляет собой обработку разных видов сигналов для того, чтобы их отфильтровать, измерить или сжать, а также создать аналоговые сигналы. Аналоговые сигналы формируются путем приема информационных данных и изменение их в электронные импульсы различной амплитуды, а цифровое преобразование информации заключается в кодировании ее двоичными кодами, в которых все биты представляются двумя разными импульсами, обозначающими логический ноль и единицу. Еще можно отметить, что аналоговые сигналы могут иметь вид синусоидальных кривых, а цифровые сигналы отображаться в виде прямоугольных импульсов. Цифровая обработка сигналов применяется во многих сферах деятельности человека. В обработке сигналов и статистике оконная функция представляет собой математическую функцию, которая имеет нулевое значение за пределами некоторого выбранного интервала, обычно симметрична относительно середины интервала. Математически, когда функция или сигнал или последовательность данных "умножается" на оконную функцию, произведение также имеет нулевое значение вне интервала: остается только часть, где они перекрываются, "вид через окно". 1 Цифровая обработка сигналов Цифровая обработка сигналов заключается в получении уже оцифрованной информации, например, звуковой, видеоинформации, параметров какого-либо процесса, и дальнейшем математическом управлении ею. После этого данные возможно выразить в виде дискретной частоты, времени или иных дискретных форматах, что позволяет выполнять в дальнейшем её переработку в цифровом отображении. При практической реализации, чтобы воспринимать аналоговый сигнал и преобразовывать его в набор нулей и единиц, требуется аналого-цифровой преобразователь. Система цифровой обработки сигналов состоит из следующих базовых составляющих: 1. Вычислительное устройство, которое осуществляет математические вычисления и управляет процессами преобразования. 2. Модуль памяти, который предназначен для хранения информационных данных, которые подлежат переработке, и функционирует вместе памятью управляющей программы. 3. Модуль памяти управляющих программ, который хранит программные приложения, предназначенные для работы с информацией. 4. Модуль ввода и вывода информации. Его структура зависит от множества параметров, определяемых областью применения цифровой обработки сигналов. 2 Цифровой фильтр 2.1 Общие сведения и применение Цифровой фильтр – в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и (или) подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов. На сегодняшний день цифровые фильтры применяются практически везде, где требуется обработка сигналов, в частности в спектральном анализе, обработке изображений, обработке видео, обработке речи и звука и многих других приложениях. 2.2 Характеристика цифровых фильтров Несмотря на то, что цифровые фильтры могут быть нелинейными и нестационарными, наибольшее распространение получили линейные стационарные фильтры в силу простоты их поведения и математического описания. Линейность фильтра подразумевает, что если подать на вход арифметическую сумму отсчётов некоторых сигналов, то на выходе фильтра будет арифметическая сумма откликов фильтра на эти сигналы. Основными характеристиками стационарных линейных дискретных фильтров являются следующие: - импульсная характеристика; - комплексная частотная характеристика; - амплитудно-частотная и фазочастотная характеристики; - системная функция (передаточная функция). Импульсной характеристикой дискретного фильтра называется его реакция на единичный импульс при нулевых начальных условиях: Линейный стационарный цифровой фильтр характеризуется передаточной функцией. Передаточная функция может описать, как фильтр будет реагировать на входной сигнал. Таким образом, проектирование фильтра состоит из постановки задачи (например, фильтр восьмого порядка, фильтр нижних частот с конкретной частотой среза), а затем производится расчет передаточной функции, которая определяет характеристики фильтра. 2.3 Достоинства и недостатки Преимуществами цифровых фильтров перед аналоговыми являются: - высокая точность (точность аналоговых фильтров ограничена допусками на элементы); - стабильность (в отличие от аналогового фильтра передаточная функция не зависит от дрейфа характеристик элементов); - гибкость настройки; - лёгкость изменения; - компактность – аналоговый фильтр на очень низкую частоту (доли герца, например) потребовал бы чрезвычайно громоздких конденсаторов или индуктивностей; - повторяемость при серийной реализации и высокая идентичность характеристик. Недостатками цифровых фильтров по сравнению с аналоговыми являются: 1. Циклическая повторяемость частотных характеристик. Трудность работы с высокочастотными сигналами. Хотя полоса рабочих частот не ограничивается частотой Найквиста, равной половине частоты дискретизации сигнала, для высокочастотных сигналов применяют аналоговые фильтры, необходимые для подавления внеполосного приёма сигналов. Если на высоких частотах нет полезного сигнала, сначала подавляют высокочастотные составляющие с помощью аналогового ФНЧ, затем обрабатывают сигнал цифровым фильтром. Трудность работы в реальном времени – вычисления должны быть завершены в течение периода дискретизации. Для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, возможно дорогостоящее, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП. 2.4 Виды цифровых фильтров КИХ-фильтр – фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр) – один из видов электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Знаменатель передаточной функции такого фильтра – некая константа. БИХ-фильтр – фильтр с бесконечной импульсной характеристикой (рекурсивный фильтр, БИХ-фильтр) – электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь. Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми, так и цифровыми. 3 Фильтр нижних частот 3.1 Общие сведения Фильтр нижних частот (ФНЧ) — электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза) и подавляющий частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра. В отличие от фильтра нижних частот (НЧ), фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты. Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д. 3.2 Применение Для звуковых волн твёрдый барьер играет роль фильтра нижних частот, например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине. Электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала, а также имеют большое число других применений. Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам. Механические низкочастотные фильтры часто используют в контурах АВМ (аналоговая вычислительная машина) непрерывных систем управления в качестве корректирующих звеньев. В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также при сжатии изображений. 4 Оконные функции Оконное преобразование Фурье — это разновидность преобразования Фурье, определяемая следующим образом: 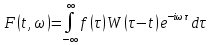 где где 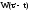 — некоторая оконная функция. — некоторая оконная функция.Существует множество математических формул, визуально улучшающих частотный спектр на разрыве границ окна. Для этого применяются преобразования: треугольное (Барлетта), синус-окно, синус в кубе, синус в 4-й степени, преобразование Парзена, Уэлча, Гаусса, Хеннинга, приподнятый косинус (Хэмминга), Чебышева, с пульсациями, Розенфилда, Блэкмана-Харриса, горизонтальное и с плоской вершиной. Прямоугольное окно (иногда известное как окно товарного вагона или окно Дирихле) является простейшим окном, эквивалентным замене всех значений последовательности данных, кроме N, нулями, что создает впечатление, что сигнал внезапно включается и выключается: w[n] = 1 В данной курсовой работе рассматривается оконная функция Бартлетта. Бартлетт использовал треугольное окно в задачах спектрального анализа: 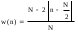 5 Ход работы 5.1 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=10 5.1.1 Исходные данные  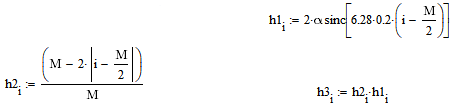 5.1.2 Прямоугольное окно 5.1.2 Прямоугольное окно 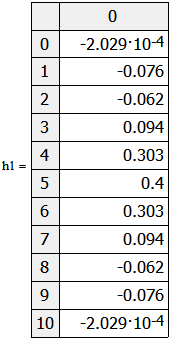 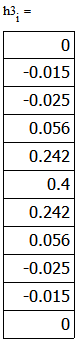 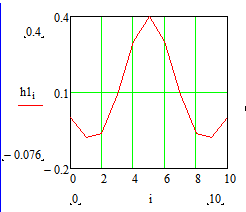  Рисунок 1. График прямоугольного Окна Бартлетта для М=10, при частоте среза равный 1000 Гц 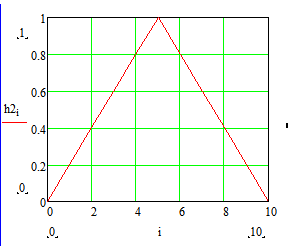  Рисунок 2. Весовая функция треугольного окна Бартлетта для М=10, частоте среза равной 1000 Гц 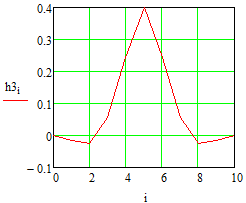 Рисунок 3. График прямоугольного Окна Бартлетта для М=10, 5  .1.3 АЧХ Прямоугольного окна .1.3 АЧХ Прямоугольного окна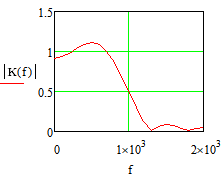 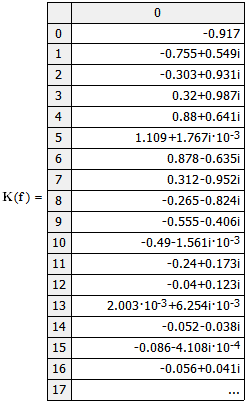  Рисунок 4. График нормированная АЧХ при М=10 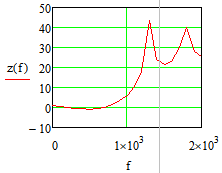  Рисунок 5. График нормированное затухание при М=10 5  .1.4 АЧХ фильтра .1.4 АЧХ фильтра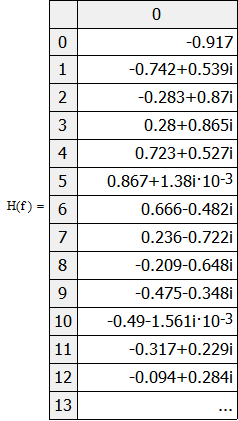 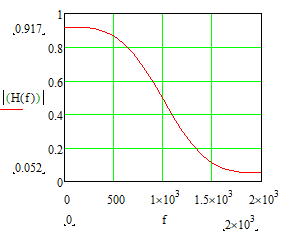  Рисунок 6. График нормированная АЧХ Бартлетта для М=10 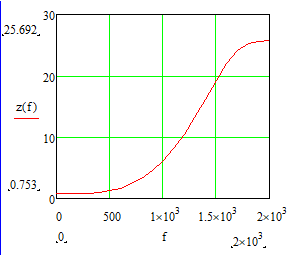  Рисунок 7. Нормированное затухание для М=10 5.2 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=20  5.2.1 Исходные данные 5.2.1 Исходные данные 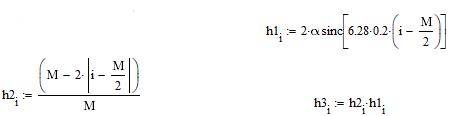 5.2.2 Прямоугольное окно 5.2.2 Прямоугольное окно 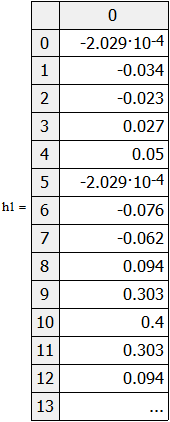  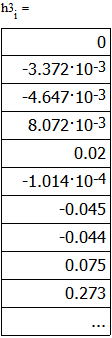 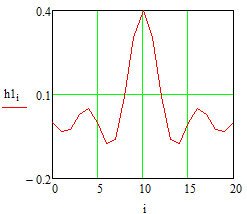  Рисунок 1 . График прямоугольного Окна Бартлетта для М=20, при частоте среза равный 1000 Гц 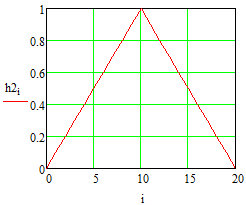  Рисунок 2. Весовая функция треугольного окна Бартлетта для М=20, частоте среза равной 1000 Гц 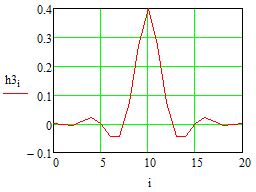 Рисунок 3. График прямоугольного Окна Бартлетта для М=20, 5 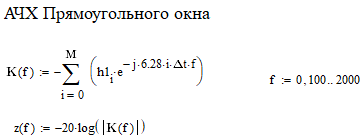 .2.3 А .2.3 А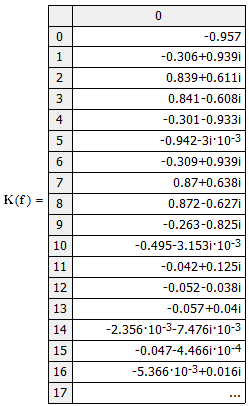 ЧХ прямоугольного окна ЧХ прямоугольного окна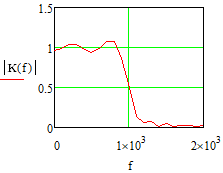 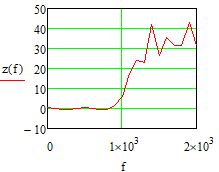   Рисунок 4. График нормированная АЧХ Бартлетта для М=20 Рисунок 5. График нормированное затухание при М=20  5.2.4 АЧХ фильтра 5.2.4 АЧХ фильтра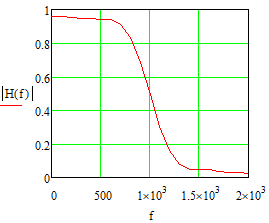 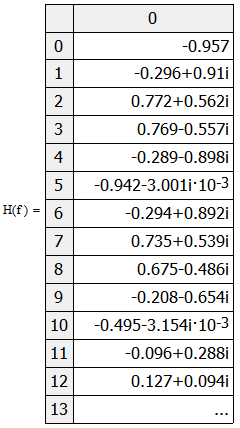  Рисунок 6. График нормированная АЧХ Бартлетта для М=20 Переходная область с ростом Н сужается 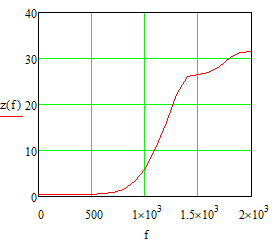  Рисунок 7. Нормированное затухание для М=20 5.3 Расчет цифрового фильтра нижних частот (ФНЧ) на основе применения треугольной оконной функции Бартлетта из разработанных данных с частотой среза 1000Гц и порядка М=100  5.3.1 Исходные данные 5.3.1 Исходные данные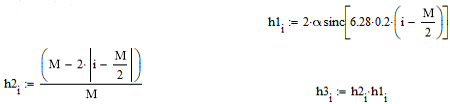 5.3.2 Прямоугольное окно 5.3.2 Прямоугольное окно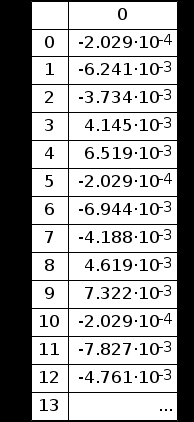  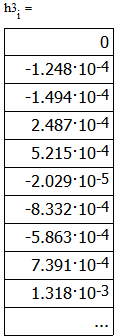 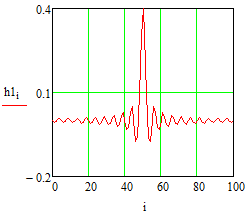  Рисунок 1 График прямоугольного Окна Бартлетта для М=100, при частоте среза равный 1000 Гц 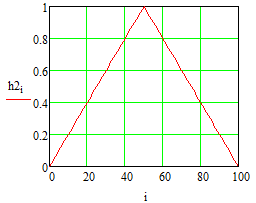  Рисунок 2. Весовая функция треугольного окна Бартлетта для М=20, частоте среза равной 1000 Гц 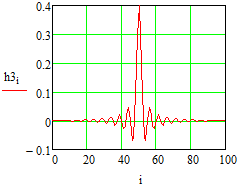 Рисунок 3. График прямоугольного Окна Бартлетта М=100 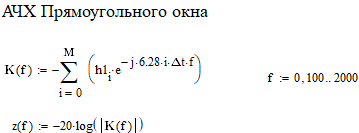 5.3.3 АЧХ прямоугольного окна 5.3.3 АЧХ прямоугольного окна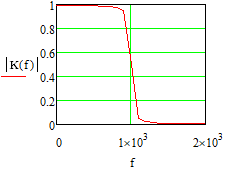  Рисунок 4. График нормированная АЧХ Бартлетта для М=100 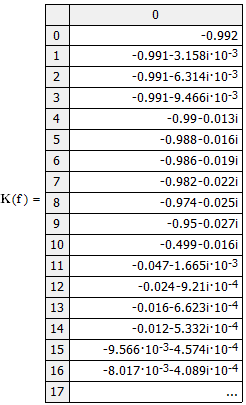 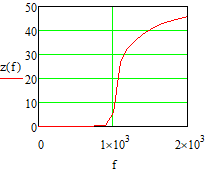  Рисунок 5. График нормированное затухание при М=100 5.4.3  АЧХ фильтра АЧХ фильтра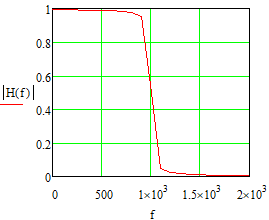  Рисунок 6. График нормированная АЧХ Бартлетта для М=100 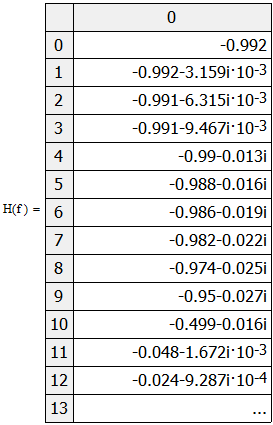 Переходная область с ростом Н сужается 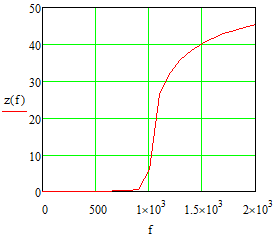  Рисунок 7. Нормированное затухание для М=100 Заключение В данной курсовой работе были изучены понятия о том, что такое цифровая обработка сигналов и цифровые фильтры. Так же на практике были выполнены расчеты фильтра нижних частот на основе применения оконной функции Бартлетта. Приобрел навыки расчета и создания цифровых фильтров оконным методом, а также научился работать с программой «Mathcad 15». СПИСОК ЛИТЕРАТУРЫ: «Цифровая обработка сигналов» учебное пособие И.И Пасечников; Министерство науки и высш. обрз. РФ, ФГБОУ ВО «Тамбов. гос. ун-т им. Г. Р. Державина». https://ru.wikipedia.org/. Время обращения (25.11.2022) Стивен Смит «Цифровая обработка сигналов». СергиенкоА.Б. «Цифровая обработка сигналов» |
