Разработка электрического способа тушения пожара на газопроводах низкого давления
 Скачать 3.36 Mb. Скачать 3.36 Mb.
|
 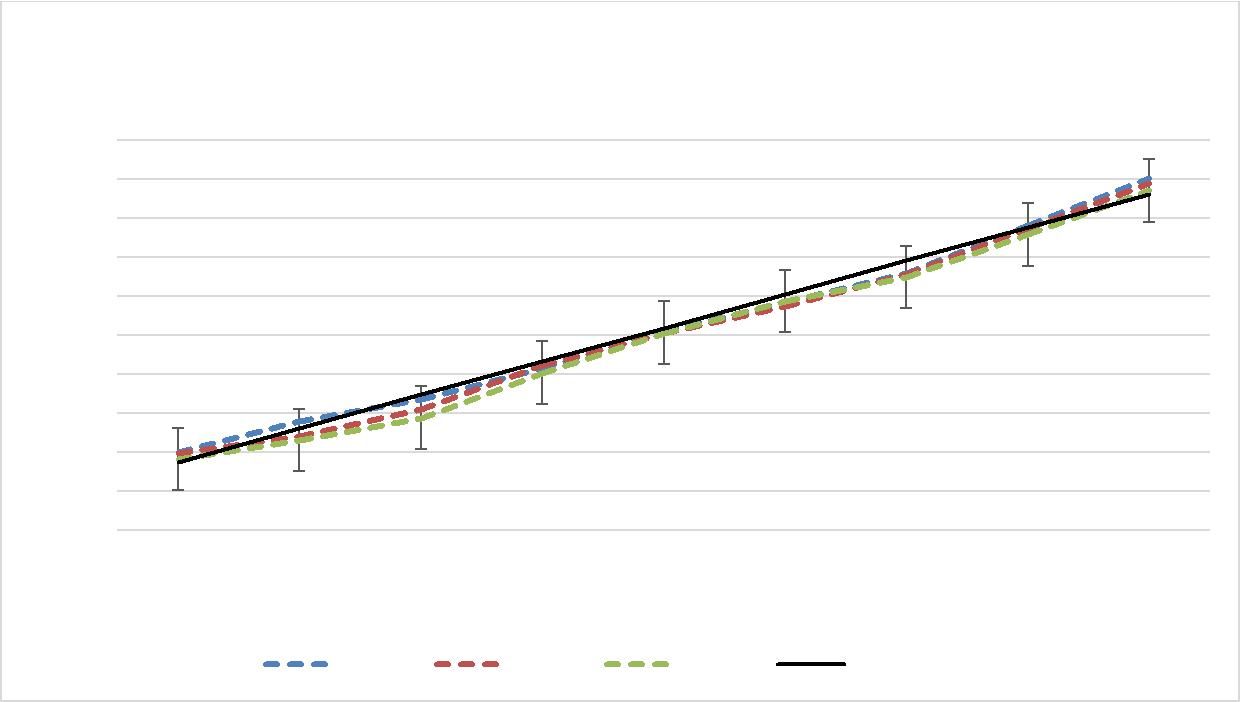 Зависимость напряжения гашения от диаметра трубки
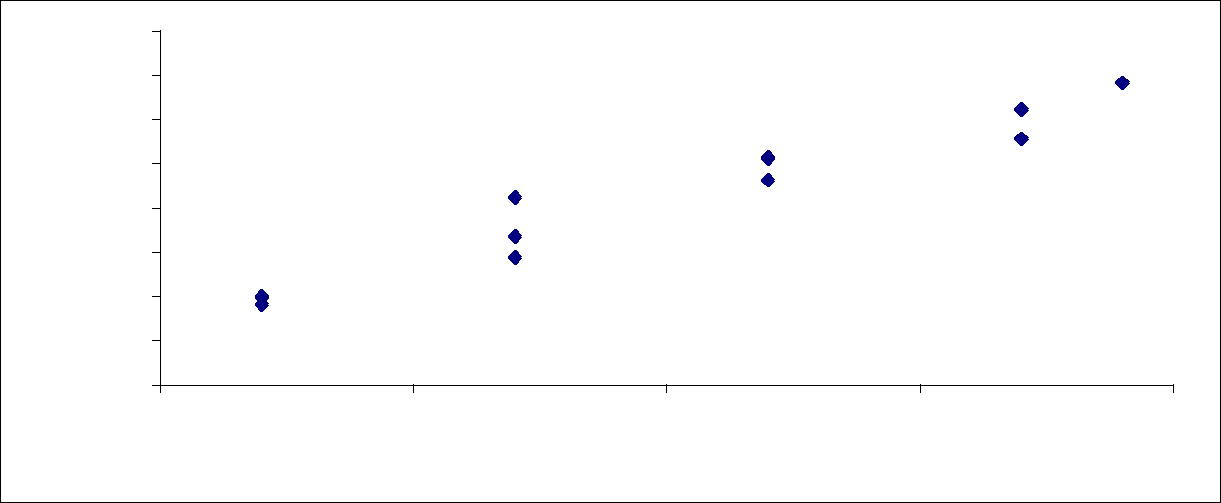
Рисунок 3.11 – Метод Монте-Карло
 качестве параметра регрессии (X2) принималась величина межэлектродного расстояния, а в качестве (X1) – диаметр газовой трубки. Из графика (Рисунок 3.10), видно, что с увеличением межэлектродного расстояния на 1 см, требуемое напряжение гашения возрастает на 1,71 кВ, что указывает на равномерное увеличение требуемого напряжения гашения от межэлектродного расстояния и их прямую зависимость. Разница между напряжениями гашения при различных давлениях газа в максимальных и минимальных значениях составляет от 3,1 до 4,7%, что находится в пределах абсолютной погрешности измерений. сравнении с предыдущими опытами напряжение гашения увеличилось на 15,76 %. Проведено моделирование электрического поля, образующегося между электродами при напряжении 43,57 кВ и 45,18 кВ соответственно, (Рисунок 3.13, 3.14). 58 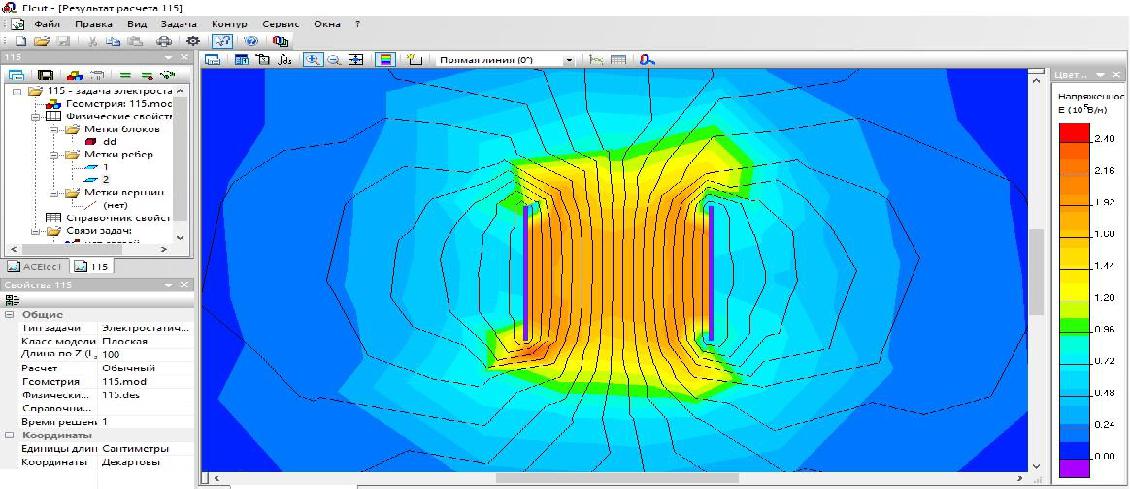 Рисунок 3.13 – Моделирование электрического поля между электродами при гашении пламени на расстоянии 25 см и диаметре 10 мм газовой трубки 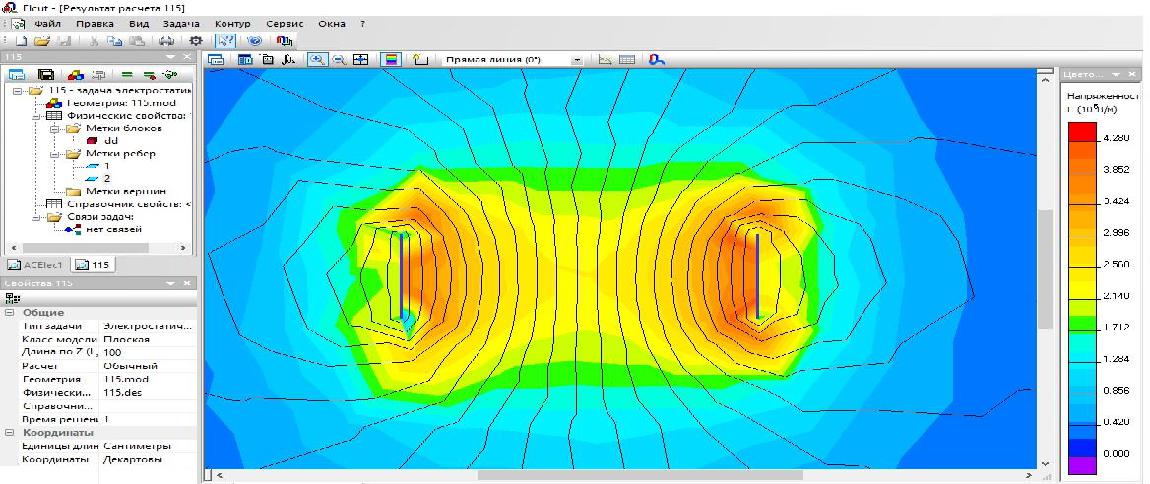 Рисунок 3.14 – Моделирование электрического поля между электродами при гашении пламени на расстоянии 25 см и диаметре 25 мм газовой трубки Таким образом, на основании экспериментальных данных, получена линейная зависимость напряжения гашения от межэлектродного расстояния при воздействии на модель газопровода (при диаметре газовой трубки от 10 до 25 мм) электрического поля напряжением до 50 кВ. Результаты экспериментов по определению зависимости напряжения гашения от межэлектродного расстояния при тушении пламени на модели газопровода с изменяющейся площадью электродов 25, 100 и 400 см2, отображены на рисунке 3.15, и в таблице 3.9. 59 Таблица 3.9 – Результаты исследований при площади электродов 25, 10, 400 см2
 3.1.6. Обработка результатов измерений. Корреляционный анализ Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия. Другим статистическим критерием является коэффициент множественной детерминации R2. Таблица 3.10 – Обработка результатов
 
Среднеквадратическое отклонение: σ(x) = 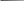  σ(y) = 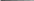  Для отбора значений, необходимых для обработки результатов методом регрессии был применен метод «Монте-Карло» (Рисунок 3.16). помощью метода «Монте-Карло» получены необходимые значения для проведения регрессии, в результате которой определен вид зависимости ( Рисунок 3.17). 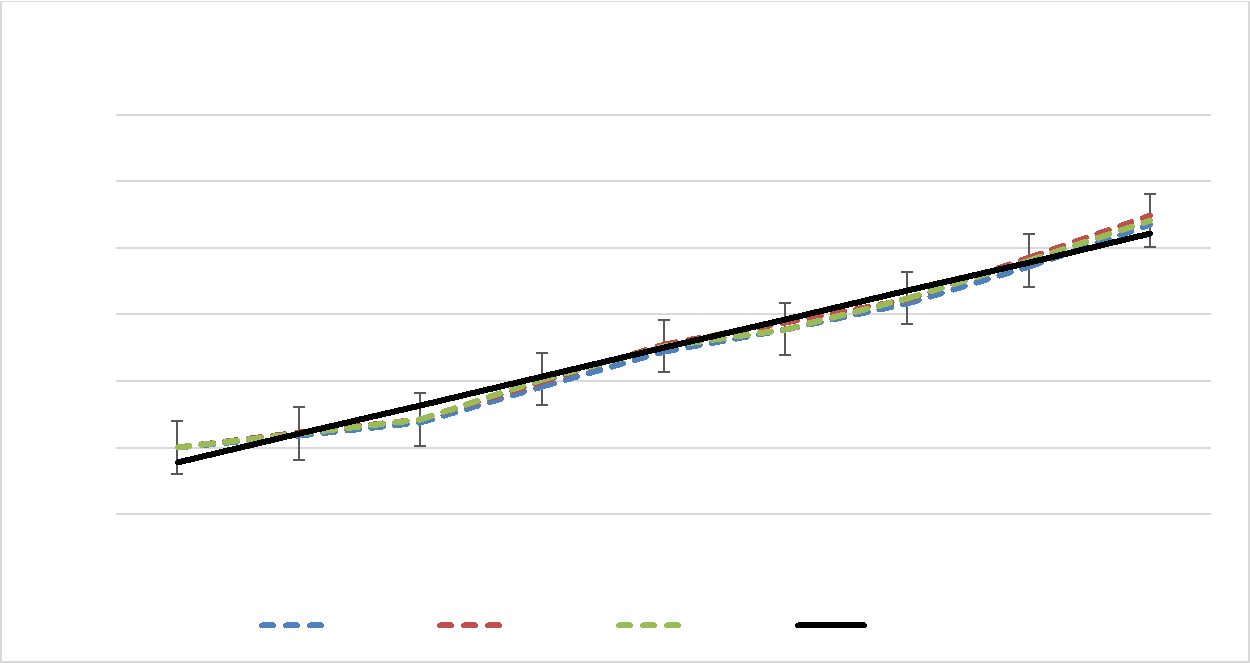
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
