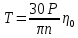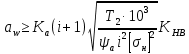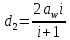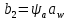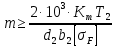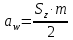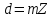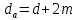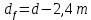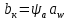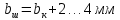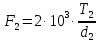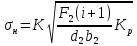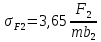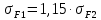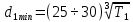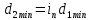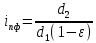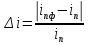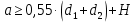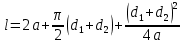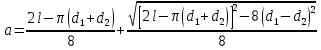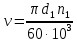Разработка механической части привода главного движения станка мод мод. 1П756ДФ3
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
5 Расчет мощностей и крутящих моментов При расчете крутящих моментов необходимо учитывать потери мощности при передачи энергии. Для этого, примем за КПД соответствующих видов передач следующие значения: 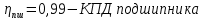 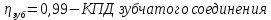  Крутящий момент определяется по формуле (12):
где P – передаваемая мощность; n – частота вращения вала (об/мин). Мощность на валу I: 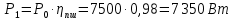 Мощность на валу II: 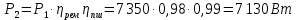 Мощность на валу III: 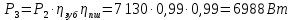 Мощность на валу IV: 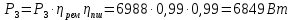 Момент на валу I: 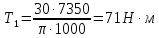 Момент на валу II: 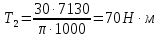 Момент на валу III: 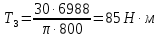 Момент на валу IV: 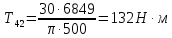 6 Расчет геометрических параметров зубчатых передач Формула для расчета межосевого расстояния (13):
где 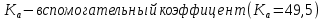 ; ;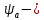 коэффицент ширины венца ( коэффицент ширины венца (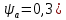 ; ;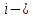 передаточное число передачи; передаточное число передачи;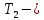 крутящий момент на тихоходном валу; крутящий момент на тихоходном валу;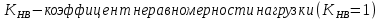 ; ;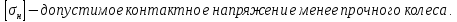 Делительный диаметр колеса можно найти по формуле (14):
где 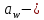 межосевое расстояние; межосевое расстояние;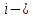 передаточное число передачи. передаточное число передачи.Для нахождения ширины венца колеса применяется формула (15):
где 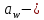 межосевое расстояние; межосевое расстояние;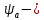 коэффицент ширины венца ( коэффицент ширины венца (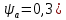 . .Модуль зацепления передачи рассчитывается по формуле (16):
где 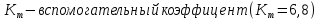 ; ;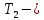 крутящий момент на валу колеса; крутящий момент на валу колеса;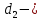 делительный диаметр колеса; делительный диаметр колеса;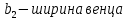 ; ;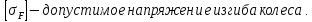 После расчета по формуле (16), модуль округляется до значения из стандартного ряда.   Рисунок 6.1 – Ряд стандартных значений модуля зубчатых колес Значение межосевого расстояния уточняется с помощью выражения (17):
где 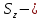 сумма зубьев зацепления; сумма зубьев зацепления;m 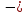 модуль зацепления. модуль зацепления.После расчета параметров зацеплений, вычисляются геометрические параметры зубчатых колес. Делительный диаметр рассчитывается по формуле (18):
Диаметр вершин зубьев – по формуле (19):
Диаметр впадин зубьев – по формуле (20):
Ширина венца колеса рассчитывается по формуле (21):
Ширина венца шестерни – по формуле (22):
Расчет В данной коробке передач имеются 3 зубчатых зацепления. По формуле (13), находим межосевые расстояния: 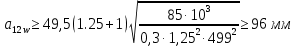 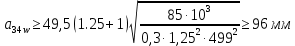 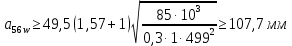 Находим расчетные делительные диаметры колес по формуле (14): 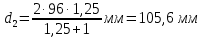 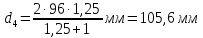 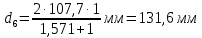 Рассчитываем ширину венцов колеса по формуле (15): 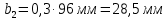 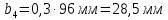 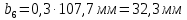 Находим расчетные модули по формуле (16): 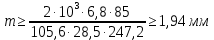 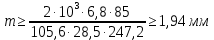 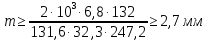 Значение модуля выбираем одинаковым для всех зацеплений, округляя большее число до одного из стандартных (первый ряд предпочтительнее). Принимаем: 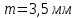 Пересчитываем значение межосевого расстояния по формуле (17): 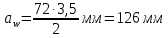 Затем, по формулам (18) – (22), рассчитываем геометрические параметры зубчатых колес: Таблица 6.1 – Параметры шестерни 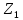 и колеса и колеса 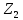
Таблица 6.2 – Параметры шестерни 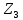 и колеса и колеса 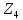
Таблица 6.3 – Параметры шестерни 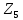 и колеса и колеса 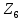
7 Проверочные расчеты на прочность Расчитанные в этом пункте напряжения не должны превышать максимальных, полученных в пунке 4. Для нахождения окружной силы зубчатых колес используется формула (23):
где 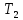 – момент кручения на колесе; – момент кручения на колесе;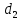 – диаметр колеса. – диаметр колеса.Формула (24) используется для нахождения контактных напряжений:
где 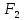 – окружная сила колеса; – окружная сила колеса;i – передаточное отношение зубчатой передачи; K – вспомогательный коэффицент (K = 436); Kp – коэффицент нагрузки (Kp = 1,27) ; d2 – диаметр колеса; b2 – ширина зубчатого венца. Напряжения изгиба зубьев определяются по формулам (25) и (26). Напряжение изгиба колеса – по формуле (25):
Напряжение изгиба шестерни – по формуле (26):
где m – модуль зубчатого колеса; b2 – ширина зубчатого венца; 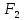 – окружная сила колеса. – окружная сила колеса.По формуле (23), рассчитываем окружуную силу колес: 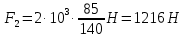 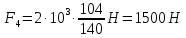 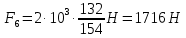 По формуле (24), находим контактное напряжение:  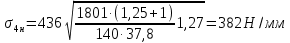 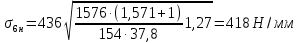 По формуле (25), напряжения изгиба: 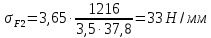 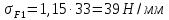 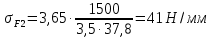 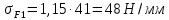 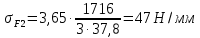 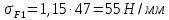 Полученные значения меньше минимально допустимых для колес: 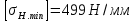 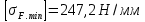 8 Расчет поликлиноременных передач 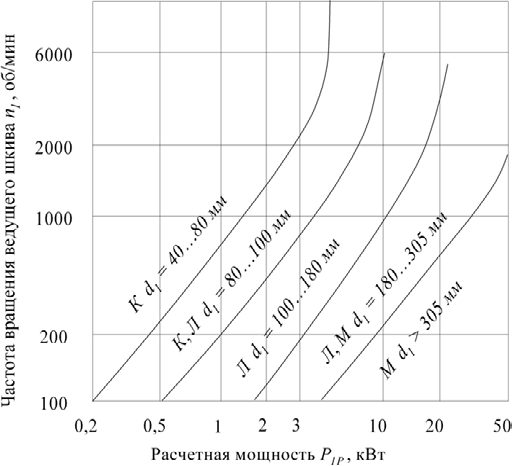  Рисунок 8.1 – Номограмма для определения типа сечения ремня Расчет начинается с определения типа сечения ремня и определения диапазона диаметров шкивов по номограмме (рис. 8.1), с помощью мощности и частоты вращения на ведущем шкив Затем, необходимо найти минимальный диаметр ведущего шкива с помощью формулы (27):
где 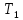 – момент на ведущем шкиве. – момент на ведущем шкиве.После этого необходимо приблизительно определить диаметр ведомого шкива, формула (28):
где 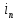 – необходимое передаточное отношение. – необходимое передаточное отношение. Рисунок 8.2 – Стандартный ряд диаметров шкивов Отношение передачи рассчитывается по формуле (29):
где 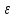 – коэффициент скольжения ( – коэффициент скольжения (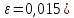 . .Отклонение фактического передаточного числа от расчетного находится по формуле (30):
где 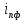 – фактическое передаточное отношение; – фактическое передаточное отношение;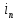 – требуемое передаточное отношение. – требуемое передаточное отношение.Межосевое расстояние клиноременной передачи рассчитывается по формуле (31):
где H – высота сечения поликлинового ремня. По формуле (32), находится расчетная длина поликлинового ремня:
Значение длины округляется до ближайшего из стандартного ряда (рис. 8.3):   Рисунок 8.3 – Стандартный ряд длин ремня Формулой (33) уточняется значение межосевого расстояния:
Угол обхвата шкива рассчитывается по формуле (34):
Скорость ремня рассчитывается по формуле (35):
где 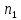 – частота вращения ведущего шкива. – частота вращения ведущего шкива.Число клиньев ремня можно найти по формуле (36):
где 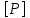 – приведенная мощность для ремня с десятью клиньями (зависит от (35)); – приведенная мощность для ремня с десятью клиньями (зависит от (35));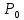 – номинальная мощность двигателя. – номинальная мощность двигателя.Формула (37) позволяет найти площадь поперечного сечения ремня:
где p – шаг ремня; H – толщина ремня; h – высота профиля клина. Последний параметр – сила давления ремня на вал, формула (38):
где 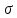 – допускаемое напряжение ( – допускаемое напряжение (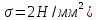 . . |